So wie bei der poten­tiellen Energie, muss man sich bei der Betrach­tung auf einen Bezugs­punkt beziehen, in diesem Fall einen Referenz­zustand. Von diesem Punkt oder Zustand aus­gehend, betrach­tet man im p-V-Diagramm den Weg zu dem jewei­ligen Punkt, an dem man sich gerade befindet. Und so sagt man, die Entropie an einem Auf­punkt A ist das Integral vom Referenz­punkt O bis zu diesem Auf­punkt A.

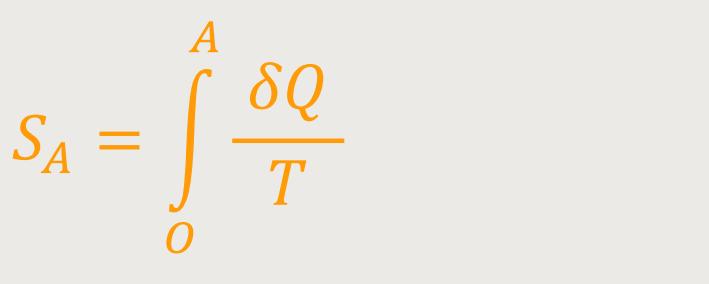
Das nennt man dann die Entropie des Zustandes A. Der Weg O → A muss aller­dings ein rever­sibler Weg sein, denn das Ganze gilt nur für reversible Prozesse. Der Referenz­punkt O ist ein fest­gelegter Referenz­zustand. Das kann zum Beispiel das Gas bei Normal­bedingungen sein. Oft wählt man in diesem Zusammen­hang einen Punkt beim absoluten Null­punkt.

Halten wir fest, die Entropie wird als eine Art Potential ein­geführt, ver­gleich­bar mit der poten­tiellen Energie in der Mechanik. Da gab es in ähn­licher Weise den Aspekt der Weg­unab­hängig­keit der Arbeit, und es wurde die Arbeit von einem Referenz­punkt bis zu dem betrach­teten Punkt als poten­tielle Energie bezeichnet.

Jetzt haben wir wieder eine Weg­unab­hängig­keit, diesmal aber mittels Integral δQ /T, und führen in ent­spre­chender Weise ein Poten­tial ein. In diesem Fall gehen wir vom Referenz­punkt O zum betrach­teten Auf­punkt A. Und dieses Poten­tial wird in der Thermo­dynamik als „Entropie” bezeich­net. Anders als bei der Wärme­menge ist die Entropie „S“ eine Zustands­größe, die nicht davon abhängt, längs welchen Weges man vom Referenz­punkt O zum Aufpunkt A gekommen ist. Es muss nur ein rever­sibler Weg sein, damit dieses Integral auch gebildet werden kann. Und wenn der Prozess einen geschlos­senen Weg durch­läuft, kompen­sieren sich alle δQ /T entspre­chend weg.

Das ist genau das, was wir bereits im vor­herigen Kapitel betrachtet haben. Diese δQ /T längs eines geschlos­senen Weges müssen in Sum­me wieder Null ergeben. Das heißt, der Carnot-Prozess, der ja einen geschlos­senen Weg beschreibt, beginnt mit einer gewissen Entropie. Sie ist nur bis auf eine Konstante definiert, so wie auch die poten­tielle Energie bis auf eine Konstante definiert ist.

Man betrachtet anschlie­ßend im p-V-Diagramm ein Teil­stück von Punkt 1 nach Punkt 2, welches dann ΔQ_W /T_W ent­spricht. In ent­gegen­gesetzte Richtung von Punkt 3 nach Punkt 4 ergibt sich dann ein −ΔQ_K /T_K. Somit ist die Summe der redu­zierten Wärmen letzt­lich wieder gleich Null.

Im Gegen­satz zu den Wärme­mengen, haben sich die redu­zierten Wärmen weg­kompen­siert. Das heißt, nach einem solchen Zyklus ist das System wieder bei der glei­chen Entropie ange­langt. Anfäng­lich war diese Über­legung vielen Physikern mehr als suspekt. Und es hat Jahr­zehnte gedauert, bis Boltzmann dann mit seiner statis­tischen Inter­pretation dem ganzen einen anderen Blick­winkel ver­liehen hat. Aber dazu kommen wir später noch.

Wir wollen noch einen weiteren wich­tigen Punkt heraus­stellen, und zwar wenn man ein thermisch isoliertes System betrachtet. In einem solchen System werden die Wärme­mengen ΔQ immer gleich Null sein. Es wird ja keine Wärme zuge­führt und auch keine abge­führt. Insofern kann sich gerade wegen des rever­siblen Prozesses auch die Entropie nicht ändern. Im Gegen­satz zu den Wärme­mengen hat die Entropie einen bestimmten Wert. Also gilt für die Wärme­mengen:

Dementsprechend ergibt sich für die Entropie in reversiblen Prozessen:

Das ist nicht gleich­bedeutend mit dem Wert „Null“, sondern damit soll ledig­lich aus­gedrückt werden, dass sich beides in Summe nicht ändert, sondern viel­mehr erhalten bleibt. Also, die Entropie ändert sich nicht bei rever­siblen Prozessen in thermisch abge­schlos­senen Systemen.

Wir wollen uns aber nicht nur auf rever­sible Prozesse beschränken. Wie ver­hält sich zum Beispiel ein irre­versibler Prozess?

Als einen typischen irre­versiblen Prozess betrachtet man insbe­sondere den Jouleschen Expansions­versuch.

Hierzu denkt man sich wieder einen zylin­drischen Behälter, der mit wärme­isolierendem Material umgeben ist, also ein thermisch isoliertes System. Im Zylinder befindet sich eine Abtren­nung mit einem Ventil, welches man schließen und öffnen kann. Durch die zwei Kammern ergibt sich ein Volumen V₁ und V₂. Zunächst befindet sich nur im Volumen V₁ ein ideales Gas. Dann wird das Ventil geöffnet, und das Gas strömt hin­über in das andere Volumen V₂. Das geschieht solange, bis der Druck in beiden Kammern aus­geglichen hat. Da bei diesem Zylinder jetzt kein Kolben vor­handen ist wird somit auch keine Arbeit geleistet.

Die experi­mentelle Erfah­rung zeigt, dass bei freier Expansion keine Tempe­ratur­änderung zu ver­zeichnen ist. Somit ändert sich auch nicht die innere Energie, denn die ist ja von der Tempe­ratur ab­hängig. Halten wir fest, hier ändert sich weder die Tempe­ratur noch die innere Energie. Zudem hat man hier einen irre­versiblen Prozess.

Denn wenn sich das Gas verteilt hat, und man anschlie­ßend das Ventil wieder schließt, bleibt der neue Zustand erhalten. Also auch hier sieht man, das funk­tioniert nur in eine Richtung. Könnte man aller­dings einen Kolben ver­schieben, dann wäre es mög­lich, den ursprüng­lichen Zustand zu erhalten. Das ist ein ganz ent­schei­dender Unter­schied. Aber uns interes­siert ja ins­besondere, wie es um die Entropie steht? Bisher war sie nur definiert für reversible Prozesse.

Wir können bei unserem gedachten Experiment eine Erwei­terung vor­nehmen. Statt ein Ventil zu öffnen, führen wir einen Ersatz­prozess durch. Wir schieben jetzt statt des Ventils einen Kolben herüber, und führen so viel Wärme­menge zu, dass auch die Tempe­ratur konstant bleibt. Also das System verrichtet dann Arbeit, aber es soll eine isotherme Expansion sein.

Wenn sich in dem System ein Kolben wegbewegt, dehnt sich das Gas aus. Die Mole­küle trommeln zwar nach wie vor an die Kolben­fläche, aber die Energie wird kleiner. Dement­spre­chend wird auch die Tempe­ratur ab­nehmen. Um die Tempe­ratur aber konstant zu halten, muss von außen eine Wärme­menge ΔQ zuge­führt werden. Es muss betrags­mäßig genau so viel Wärme­menge ΔQ zuge­führt werden, wie Arbeit −ΔW ver­richtet wird.

Letzten Endes kommt man bei dem Ersatz­prozess eben­falls auf das Gesamt­volumen V₁ + V₂. Man hat den gleichen Zustand wie im Beispiel mit dem Ventil, nur der Weg dorthin, war ein anderer. Und zusätz­lich haben wir jetzt einen rever­siblen Vorgang. Damit ist es uns möglich, die Entropie­änderung ΔS aus­zurechnen.

Wenn also die zuge­führte Wärme­menge gleich der abge­führten Arbeit ist, bedeutet das:

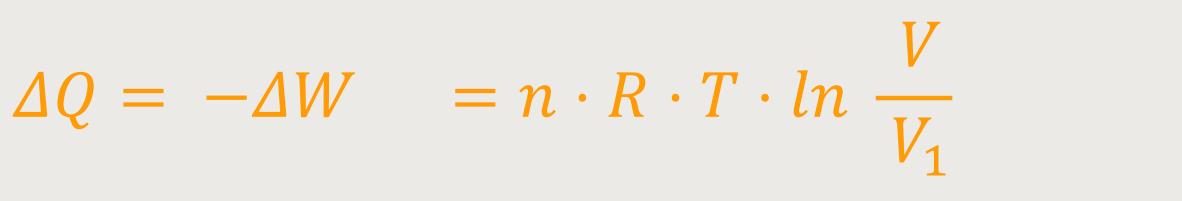
Die Wärme­menge ΔQ, die man bei diesem rever­siblen Ersatz­prozess hinein­steckt, führt zum gleichen End­zustand. Wenn aber die Entropie wirk­lich eine Zustands­größe ist, dann muss sie für das expan­dierte System mit dem Kolben den gleichen Wert haben, wie bei dem System mit dem Ventil. Da jetzt das System rever­sibel ist, lässt sich die Entropie­änderung des Ersatz­prozesses ermitteln.

Da die Entropie­änderung und die Ände­rung der Wärme­menge mit­einander in Beziehung stehen, brauchen wir beides nur durch die Tempe­ratur dividieren, und erhalten damit:

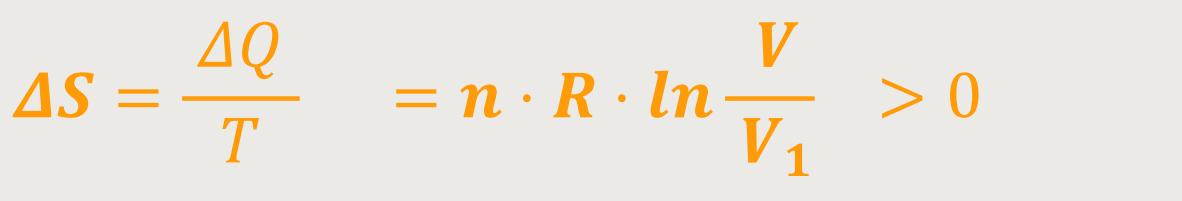
Damit erhält man eine Entropie­änderung > 0, obwohl in obigem Beispiel mit dem Ventil gar keine Wärme­menge zuge­führt wurde. Im zweiten Fall nimmt die Entropie aller­dings zu, weil im Beispiel mit dem Kolben dagegen Wärme­menge zuge­führt wurde.

Bei einem thermisch isolierten System ist die Wärme­menge ΔQ immer Null. Dann müsste ja ΔQ /T auch Null sein. Aber das gilt nur für rever­sible Prozesse. Das Beispiel mit dem Ventil ist aber irre­versibel.

Das heißt, wenn ΔS = 0 ist, gilt das nur für reversible Prozesse in thermisch abge­schlos­senen Systemen. Wenn man dagegen einen irre­versiblen Prozess hat, kann man die Entropie auf diese Weise nicht ermitteln. Obwohl der gleiche End­zustand durch einen rever­siblen Ersatz­prozess erreicht werden kann. Man muss halt nur einen Kolben langsam heraus­schieben, und gleich­zeitig die not­wendige Wärme­menge ΔQ hinzu­fügen, um letzt­lich durch isotherme Expansion den gleichen End­zustand wie beim Beispiel mit dem Ventil zu erreichen. Daher muss die Berech­nungs­grund­lage für die Entropie­änderung ΔS richtig sein, weil hier ein rever­sibler Prozess die Grund­lage bildet.

Und wenn man einen irre­versiblen Prozess hat, muss man trotz­dem auf das Gleiche ΔS kommen. Daraus folgt: ΔS > 0 obwohl ΔQ = 0. Wie ist das zu inter­pretieren?

Demnach gilt für irre­versible Prozesse, dass die Entropie­änderung nicht ΔS ≠ 0, sondern > 0 sein wird. Bei Zustands­ände­rungen in thermisch isolierten Systemen ist die Entropie­änderung dagegen ΔS ≥ 0, wobei das Gleich­heits­zeichen für reversible Prozesse steht. Denn bei irre­versiblen Prozessen wird die Entropie „S“ ständig zunehmen. Somit wird die Entropie nie kleiner, sie kann höchstens gleich bleiben. Im Fall irre­versibler Vor­gänge nimmt sie zu. Und das ist wieder eine Folge des Zweiten Hauptsatzes.

Doch wenn die Entropie immer nur größer werden kann, dann steuert das Universum einer merk­würdigen End­situation zu. Wenn dem so wäre, wie zahl­reiche Physiker und Astro­nomen befürchten, hätten wir auf Dauer keine Zukunft. Hier spielt jetzt die Boltzmannsche Inter­pretation eine wesent­liche Rolle, zu der wir im nächsten Kapitel noch kommen. Dann wird man ver­stehen, was diese aus prak­tischen Erwä­gungen wie ein Poten­tial ein­geführte Größe „S” für eine wichtige funda­mentale Bedeutung hat.

Nun noch ein paar Schlussworte zum Begriff „Entropie”.

Der Begriff kommt vom grie­chischen entripain, und heißt so viel wie umdrehen. Die Entropie hat etwas damit zu tun, ob man etwas um­drehen kann, also ob ein Prozess rever­sibel ist, sprich ob man einen Aus­gangs­zustand noch einmal erreichen kann. Streng­genommen sagt die Thermo­dynamik, die Entropie nimmt immer zu, also die Fähig­keit etwas umzu­drehen wird immer kleiner und kleiner.

Die Entropie ist aber ein Spezial­aspekt der Thermo­dyna­mik und hat mit einer Viel­zahl von Mög­lich­keiten zu tun. Ein geordne­ter Zustand hat eine niedrige Entropie. In den vor­herigen Bei­spielen haben wir ja gesehen, dass man nach Mischen eines Mediums nie wieder den geordne­ten Anfangs­zustand erreichen kann. Jeder Zustand, der danach kommt ist eine weitere Mög­lich­keit. Und weil die Mög­lich­keiten der Unord­nung viel größer sind als die Mög­lich­keiten der Ordnung, ver­größert sich theore­tisch die Entropie.

Die Entropie ist eine soge­nannte exten­sive Größe. Sie hängt mit der wirk­lichen Aus­dehnung eines Systems zusammen. Wenn das Universum ständig expan­dieren würde, ver­größert sich zwangs­läufig die Entropie. Sie ist demnach riesig und wird in Zukunft noch größer werden. Ein Zustand der geordnet ist, ist demnach ein Zustand niedriger Entropie. Und ein Zustand der ungeord­net ist, ist ein Zustand hoher Entropie. Der Zweite Haupt­satz, nämlich dass die Entropie immer zunimmt, gilt nur für irreversible Systeme. Also Systeme die von der Umwelt thermisch isoliert sind. Die Erde ist dagegen nicht von der Umwelt abge­schlossen. Sie ist quasi ein kosmischer Durch­lauf­erhitzer.

Die Sonne ist mit ihren etwa 6000 °C sehr heiß. Das Universum ist mit 2,7 Kelvin dagegen sehr kalt. Die Erde liegt mit ihrem Tempe­ratur­bereich genau dazwischen. Lebens­formen gibt es auf der Erde nur deshalb, weil diese auf der Erde Energie auf­nehmen und auch Energie wieder abgeben. Wenn man Energie aufnimmt ist man in der Lage, einen Zustand niedrigerer Entropie zu erhalten.

Entropie hat auch etwas mit Informa­tion zu tun. Je geordne­ter ein Zustand ist, umso mehr Infor­mation enthält er. Die Ent­wicklung von Molekülen ist daher etwas ganz besonderes. Aber thermo­dyna­misch gesprochen ist das nur eine Winzig­keit. Um sich vor­zustellen, was es mit den Infor­mationen auf sich hat, gibt es einen schönen Vergleich:

Hierzu betrachtet man ein Glas Bier mit etwas Schaum oben­drauf. Schaum scheint auf den ersten Blick etwas völlig Ungeord­netes zu sein. Demnach müsste Schaum ein Zustand hoher Entropie sein. Nach einiger Zeit ist der Schaum wieder weg, und man sieht nur noch die klare Flüssig­keit. Alles sieht jetzt sehr schön geordnet aus. Diese Annahme ist aber ein Trug­schluss. Der Schaum zerfällt zwar zu Flüssig­keit. Der Grund ist aber, dass die Entropie bei diesem Schaum­zerfall in Form von Flüssig­keit zunimmt. Der Schaum, insbe­sondere die Blasen­wände, sind Zwangs­bedingungen an das System. Das heißt, im Schaum sind eigent­lich mehr Informa­tionen ent­halten, als in der Flüssig­keit.

Im Schaum können sich die Mole­küle nur in den Blasen­wänden bewegen, wogegen sie sich in der Flüssig­keit völlig frei bewegen können. Das heißt, die Anzahl der Bewegungs­mög­lich­keiten sind in einer Flüssig­keit viel größer, als die Mög­lich­keiten in einer Schaum­blase. Entropie hat also streng­genommen viel damit zu tun, welche Zwangs­bedingungen in einem physika­lischen System vor­herrschen. Was also Ordnung ist und was Unord­nung ist, lässt sich in vielen Fällen nicht immer ein­deutig erkennen. Und so ziehen Physiker und Astro­nomen oft vor­schnelle Schluss­folge­rungen, ohne viel­leicht den gesamten Zusammen­hang zu kennen.

Klar ist aber, dass bei offenen Systemen, also Systemen, die nicht isoliert sind, Energie zufließt und auch wieder abge­geben wird. Als Menschen nehmen wir zum Beispiel entropie­arme Dinge auf, und geben entropie­reiche Dinge wieder ab. Aber in geschlos­senen Systemen nimmt die Entropie immer zu. Um dennoch eine Entropie­reduktion zu erreichen, muss Energie zuge­führt werden. Eine Gleich­ver­teilungs­situation ist eine Situation höchster Entropie, also geringster Infor­mation. In dem Moment aber, wo Energie in das System rein­kommt, gibt es auf einmal die Mög­lich­keit, die Entropie zu verringern.

Aller­dings muss dann die Energie von außen kommen. Erst dann kann das System im Innern eine niedri­gere Entropie haben. Damit ist auch klar, wie im Universum über­haupt etwas ent­stehen kann. Es gibt eine äußere Energie­quelle, im Allge­meinen spricht man von einer Art Gravi­tations­potential, die alles strukturiert.

Ausgehend von einem Urknall würde wahn­sinnig viel Entropie erzeugt. Denn ein riesiges Volumen, aus dem das Gas ursprüng­lich kam, war daran betei­ligt. Darüber hinaus muss eine Insel mit einer niedri­geren Energie erzeugt werden, in einem Meer von Unord­nung. Und weil im Großen und Ganzen ständig alles zer­fällt, ver­treten einige die Auf­fassung, dass die Entropie nur anwend­bar sei in einem klaren physika­lisch gegebenen Sinne. Anders solle man den Begriff nicht ver­wenden. Entropie wäre eine physika­lische Aussage über die Anzahl der Mög­lich­keiten in einem physika­lisch gewählten Raum.

⇦ Kapitel Kapitel ⇨