Was passiert denn, wenn eine Schwingung nicht mehr gleichmäßig vor sich hin schwingt?

Wenn ein Gewichtsstück an einer Spiralfeder in Schwingung versetzt wird, schwingt es in einem reibungsfreien Umfeld weiter vor sich hin. Wenn man es aber in eine Reibungssituation versetzt, beispielsweise in einen Behälter mit Wasser taucht, dann wird die Schwingung immer geringer, bis man schließlich keine Schwingung mehr wahrnimmt. Es kommt also dazu, dass die Schwingungsamplitude immer kleiner wird. Solche Situationen treten in der Praxis sehr häufig auf. Wie kann man das beschreiben?

Jedes Mal, wenn man eine neue Bewegungsform anschaut, stellt sich die Frage, wie sieht die Bewegungsgleichung aus. Die Bewegungsgleichung stellt in einer Reibungssituation wie folgt dar:

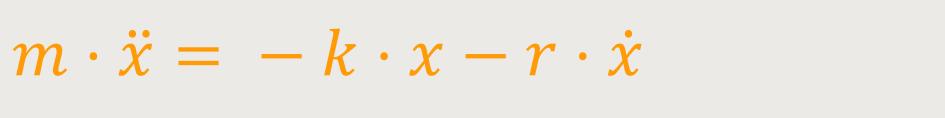
k   ist die Rückstellkonstante
r   ist die Reibungskonstante
r ·   ist ein Dämpfungsterm

Dieser Term hängt wieder mit der Geschwindigkeit der Bewegung zusammen. Je größer die Geschwindigkeit ist, desto größer wird die Reibungskraft sein.

Durch Umformen ergibt sich eine Differentialgleichung:

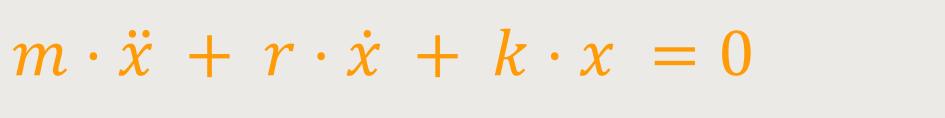
Obwohl diese Gleichung etwas komplizierter ist, kann man auch hier den komplexen Lösungsansatz machen:

Damit man später entsprechend einsetzen kann, benötigt man:

Alle drei Gleichungen enthalten die gleiche Zeitabhängigkeit und zudem konstante Vorfaktoren. Das ist der große Vorteil eines solchen Exponentialansatzes. Wenn man das jetzt in die Schwingungsgleichung einsetzt, ergibt sich daraus:

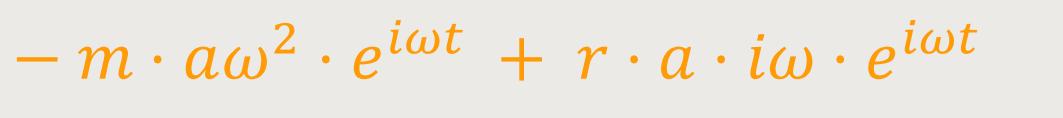
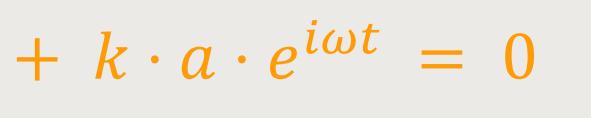
Auch hier kann man wieder durch die komplexe e-Potenz durchkürzen und erhält dadurch eine Gleichung, bei der man die Schwingung entsprechend ausrechnen kann. Und nachdem auch die Amplitude weggekürzt wurde, ergibt sich:

Wenn man jetzt noch durch −m dividiert, erhält man eine quadratische Gleichung:

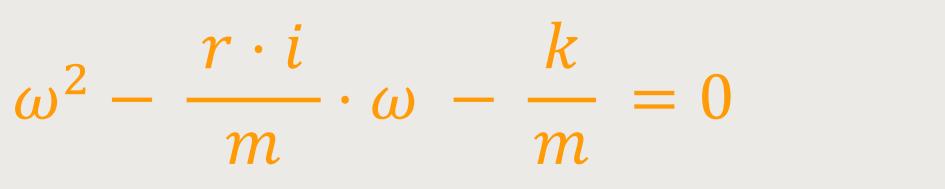
An dieser Stelle kann man gedanklich einmal ein paar Fälle durchspielen. Was wäre, wenn zum Beispiel die Dämpfung bzw. die Reibungskonstante r = Null ist?:

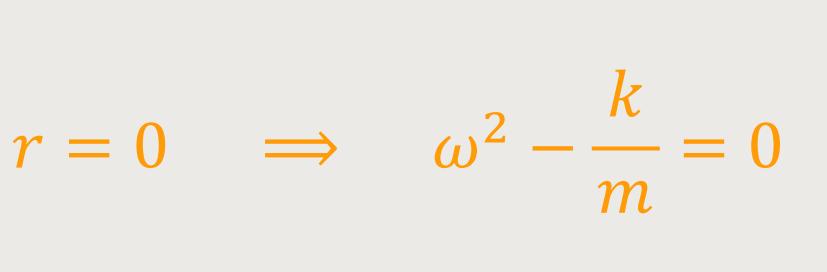
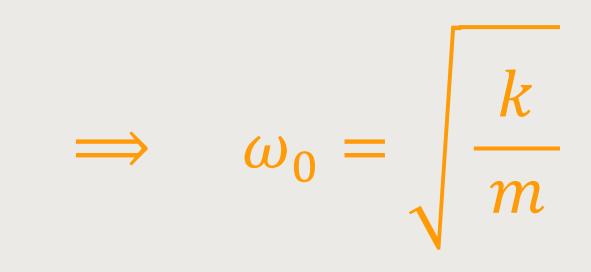
Diesen Ausdruck kennen wir bereits von der ungedämpften Schwingung (s.o.). Und was wäre, wenn die Reibungskonstante r ≠ Null ist?:

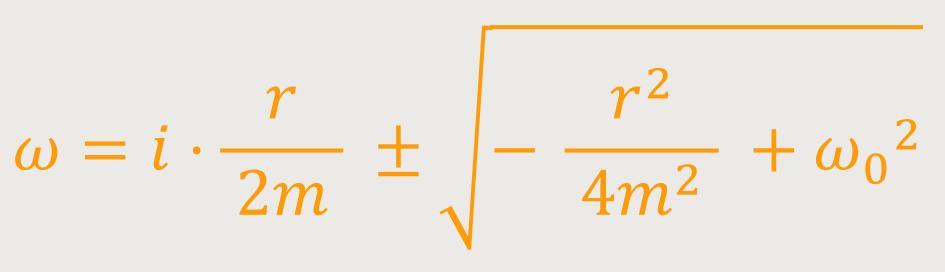
Diese Gleichung besteht wieder aus einem imaginären Teil und einer Wurzel. Wenn man jetzt aber annimmt, dass die Dämpfung nicht zu groß ist, also:

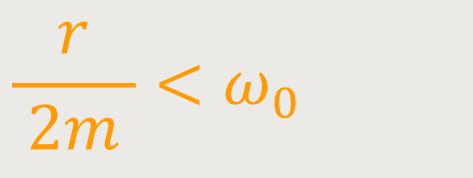
Und wenn man das jetzt in obigen Lösungsansatz einsetzt, ergibt sich für einen positiven Wurzelteil:

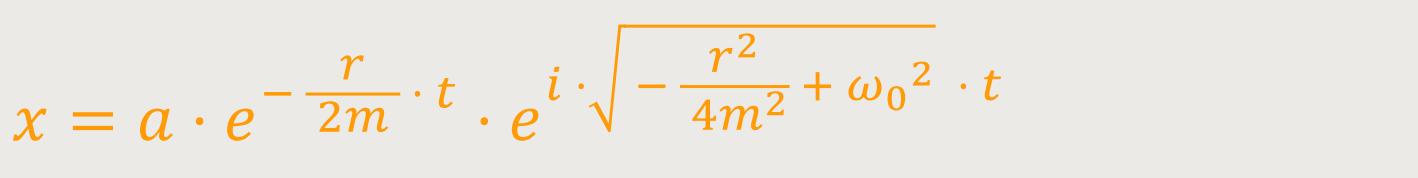
Der imaginäre Teil steht für den Rückgang der Schwingung. Der Wurzelteil entspricht der Kreisfrequenz.

Dem ersten Term der Gleichung kann man entnehmen, dass die Amplitude der Schwingung im Laufe der Zeit abnimmt. In der Zeit t = τ  = 2m /r erhält man eine Abnahme der Amplitude von a · e⁻¹ nach a /e . Man hat also eine exponentiell abnehmende Amplitude. Wir dieser Ausdruck mit einer ungedämpften Schwingung multipliziert, erhält man dadurch eine gedämpfte Schwingung. Das ist dann die Zeitkonstante für die Dämpfung.

Allerdings wird die Schwingung nie ganz auf Null zurückgehen. Sie wird nur immer geringer und ist irgendwann experimentell nicht mehr wahrnehmbar. Man kann sich aber fragen, wie lang es dauert, bis die Amplitude auf den e-ten Teil (e = 2,7), also um ca. 1/3 zurückgeht. Diese Zeit gibt dann die Zeitkonstante an und das ist gerade der Reziprokwert.

Wenn das entsprechend multipliziert wird, steht dann a · e⁻¹ da. Damit erhält man gerade die Abnahme auf den e-ten Teil. Und das ergibt letztlich eine Schwingung mit schwacher Dämpfung.

Bei einer „starken Dämpfung” hat man eine stark abfallende Schwingung. Insofern gibt es keine Periodi­zität mehr, und es schwingt nichts mehr. In diesem Fall gewinnt der erste Teil unter der Wurzel und die Zahl wird negativ. Das bedeutet wiederum, dass die ganze Wurzel negativ wird, und man erhält einen weiteren imaginären Teil.

Für die starke Dämpfung gilt analog:

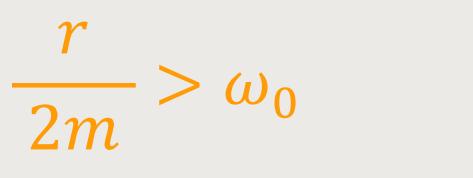
Letztlich wird der gesamte Ausdruck für die Kreis­frequenz eine rein imaginäre Zahl. Wenn das entspre­chend in die e-Potenz a · e^iωt ein­fließt, erhält man keinen reellen Teil mehr.

Das heißt, es wird nichts mehr schwingen, sondern man hat nur noch eine exponen­tielle Abkling­phase. Und das ist im Allge­meinen recht uninteressant. In so einer Situation kann dann nicht mehr von einem „Oszillator” sprechen, weil sich keine periodische zeitliche Verän­derung mehr ergibt.

Eine große starke Dämpfung aus­zeichnet sich somit dadurch aus, dass es keine Periodi­zität mehr gibt.

Was ist aber, wenn man einen „aperiodischen Grenz­fall” hat, also wenn die Frequenz und die Dämpfung gleich sind:

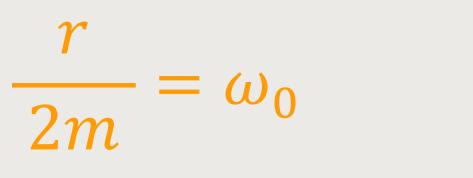
In diesem Fall sind beide Ausdrücke in der Wurzel gleich groß. Und dem­entspre­chend wird das, was unter der Wurzel steht, den Wert Null annehmen. Letzt­lich bleibt nur noch der erste Teil, sprich der imaginäre Teil übrig:

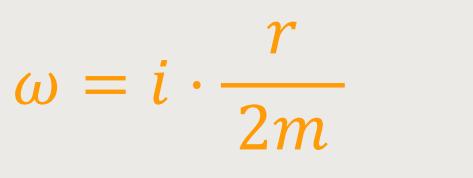
Wird der imaginäre Teil anschlie­ßend im Ansatz a · e^iωt mit i multi­pliziert, dann schwingt immer noch nichts. Das Gewicht pendelt sich viel­mehr zügig in die Gleich­gewichts­lage ein.

Das ist zum Beispiel bei Stoßdämpfern in einem Kraft­fahr­zeug sehr interessant. Sind die zu wenig gedämpft, kommt es zu unan­genehmen Schwingungen und es braucht seine Zeit, bis sich die Karosserie einge­pendelt hat. Das will man natürlich aus Komfort­gründen vermeiden.

Der aperiodische Grenzfall auszeichnet sich somit dadurch aus, dass es optimal schnell zu einer Gleich­gewichts­lage kommt.

⇦ Kapitel Kapitel ⇨