Jetzt gibt es noch eine weitere wichtige Größe. Das ist die Schwingungs­dauer. Darunter versteht man die Zeit, die ver­streicht, bis man wieder auf einen analogen Punkt bzw. homologen Punkt bei dieser Schwingung kommt. Diese Zeit nennt man T, und das ist die Schwingungs­dauer. Jetzt stellt sich die Frage, wie die Schwingungs­dauer mit der Kreis­frequenz ω zusammen­hängt.

Bevor wir darauf eingehen, betrachten wir noch kurz, wie man den Zeit­nullpunkt verschieben kann. Wenn man das umsetzt, kommt man von der Dar­stellung ωt zur Dar­stellung ωt + φ. Welchen Vorteil bringt uns das?

Wenn man zunächst den aktuellen Zeit­nullpunkt bei­behält, ergibt sich:

Re   ist der Realteil (hier von x)

Bei einer Änderung des Zeit­nullpunktes ergibt sich:

Das Argument des Kosinus (Cosinus) ωt + φ nennt man dann die „Phase”. Und das φ ist die „Phasen­verschiebung”.

Doch wie lässt sich die Schwingungs­dauer fest­stellen? Die Schwingungs­dauer T hat die Eigen­schaft, dass wenn man mit der Zeit um eine solche Strecke T fort­schreitet, wieder die gleiche Bedingung hat, wie zuvor. Das ent­spricht einem Voran­schreiten um dieses Zeit­intervall. Das bedeutet aber:

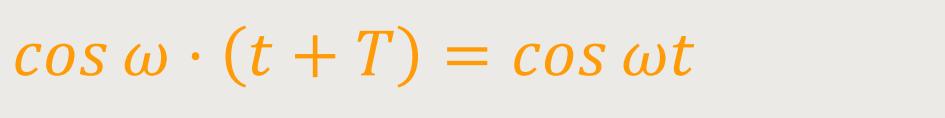
Aufgrund der Periodi­zitäten des Cosinus ergibt sich daher:

Die Schwingungs­dauer lässt sich somit darstellen als:

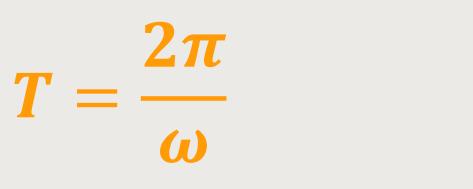
Hinweis:π steht hier im Bogenmaß (180°)

Durch Umformung erhält man eine Inter­pretation für das ω:

Was bedeutet das? 2π ist der volle Winkel, und T ist die Zeit, in der der volle Winkel durch­schritten wird. Daher ist 2π /T der Winkel, den der Vektor-Zeiger in der Zeit­einheit durch­schreitet. Dieses ω ist dem­nach nichts anderes, als die Winkel­geschwin­dig­keit des Zeigers in der komplexen Ebene. Daher nennt man dies auch die „Kreis­frequenz”.

Betrachten wir ein kurzes Rechen­beispiel: Wenn T die Schwingungs­dauer ist und zum Beispiel 1 /10 Sekunde dauert. Wie viele Schwingungen werden dann pro Sekunde stattfinden? Das Ergebnis lautet 10. Denn die Frequenz, also die Anzahl der Schwingungen pro Zeit­einheit, ist einfach 1 /Schwingungsdauer.

Die Frequenz, die wir mit ν (nu) bezeichnen, ist die Anzahl der Schwingungen pro Zeit­einheit.

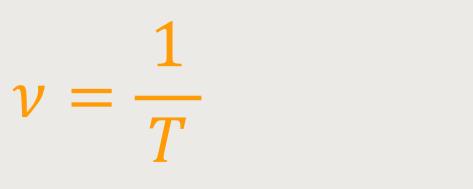
T   ist die Schwingungsdauer

Je kleiner die Schwingungs­dauer ist, desto größer wird die Frequenz.

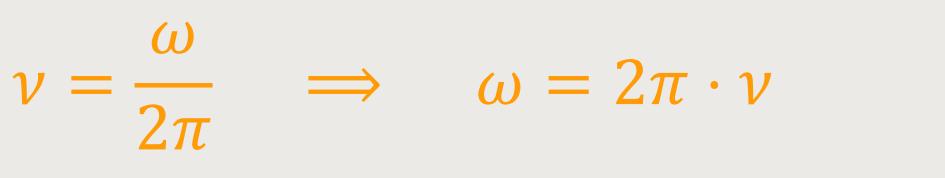
ω   ist die Kreisfrequenz
ν   ist die Frequenz

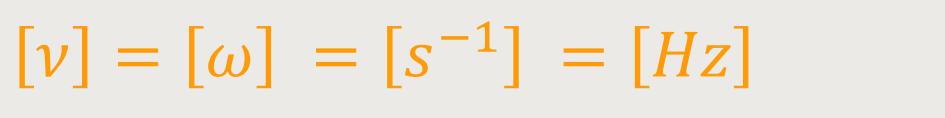
1 Hz = 1 Schwingung /Sekunde
1 MHz = 1 Mio. Schwingungen /Sekunde
1 GHz = 1 Mrd. Schwingungen /Sekunde

Als Nächstes wollen wir die Situation betrachten, wenn mehr als eine Schwingung auftritt. Also wenn es eine Über­lagerung von Schwingungen gibt.

Da gibt es verschie­dene Mög­lich­keiten. Das eine ist, man betrachtet 2 Schwingungen mit gleicher Frequenz. Diese können so angeordnet sein, dass sie zwar die gleiche Frequenz haben, und damit auch die gleiche Schwingungs­dauer, aber phasen­mäßig können sie anders liegen und auch eine andere Amplitude haben.

Würde man jetzt geradewegs mit Sinus- oder Kosinus Funktionen weiter­rechnen, hätte man es mit lästigen Additions­theoremen zu tun. Und das möchte man sich nach Mög­lich­keit ersparen. Das kann man auch, wenn man wieder auf die Zeiger­darstellung zurück­greift.

Zunächst stellt man die Situation wieder in der komplexen Ebene in einem Koordinaten­kreuz dar. Die x-Achse entspricht der reellen Achse Re und die y-Achse der imaginären Achse Im. Um den Punkt 0,0 wird in gewohnter Weise ein Kreis gezogen. Dieses Mal geht es aber um zwei Schwingungen mit unter­schied­lichen Amplituden und unter­schied­lichen Phasen­lagen. Gelöst wird das Ganze mithilfe der „Vektor­addition”, sodass die beiden Vektor-Zeiger einen neuen Zeiger ergeben.

Aufgrund dieser vektoriellen Addition der Zeiger ergibt sich sofort die Über­lagerung der beiden Teil­schwingungen. Trotz der unter­schied­lichen Amplituden und unter­schied­lichen Phasen­lagen wird wieder eine ein­heit­liche harmonische Schwingung geliefert, mit einer bestimmten Amplitude und der gleichen Frequenz. Die gleiche Frequenz bedeutet, dass alle Vektor-Zeiger starr mit­einander verbunden bleiben, während sie sich durch die komplexe Ebene drehen.

Das ist der Fall, weil sich alle Zeiger mit der gleichen Winkel­geschwindig­keit, also mit der gleichen Kreis­frequenz bewegen. Die zusammen­gesetzte Schwingung hat wieder die gleiche Frequenz, aber eine unter­schied­liche Amplitude und eine unter­schied­liche Phasen­lage im Vergleich zu den beiden Teil­schwingungen. Das gilt für den Fall gleicher Frequenz.

Wenn die Frequenz dagegen ungleich ist, schaut die Sache nicht mehr so einfach aus. In diesem Fall eignet sich auch das Zeiger­diagramm nicht mehr so gut. Denn bei zwei unter­schied­lichen Frequenzen eilt der eine Vektor-Zeiger dem anderen voraus. Dann bleibt die gesamte Vektor­anordnung nicht mehr in der gleichen Lage.

Damit man das aber trotz­dem behandeln kann, ist es manchmal zweckmäßig, wieder auf die reelle Dar­stellung über­zugehen. Das trifft insbe­sondere für den Fall zu, wenn man zwei Schwingungen mit ähnlicher Frequenz hat.

„Ähnliche Frequenz” bedeutet, dass der prozentuale relative Unter­schied zwischen den Frequenzen klein ist gegen die tatsäch­lichen Frequenzen. Wenn man das wieder 1-dimen­sional darstellt, ergibt sich für die erste Schwingung:

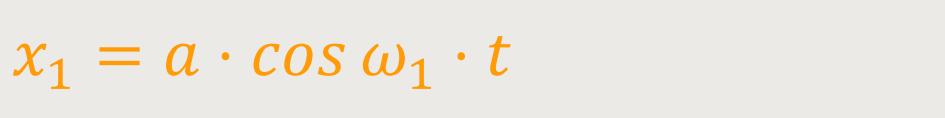
ω_₁   ist die Kreis­frequenz der ersten Schwingung

Die 1-dimensionale Darstellung für die zweite Schwingung lautet:

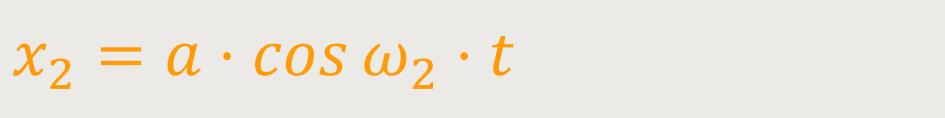
ω_₂   ist die Kreis­frequenz der zweiten Schwingung

Im nächsten Schritt geht es darum, die beiden Schwingungen zu addieren. Dies geschieht auf Basis des Additions­theorems:

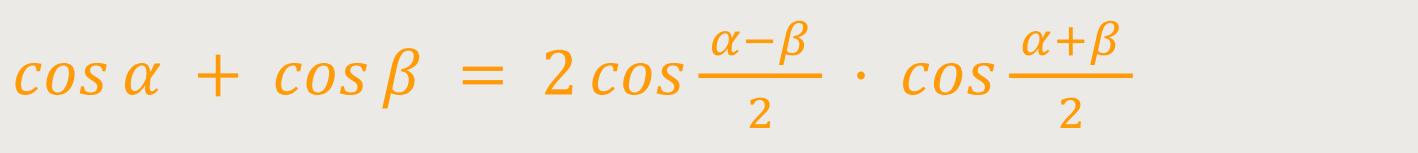
Für die gesamte Schwingung gilt somit:

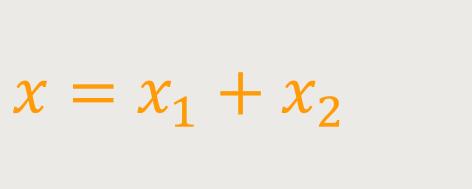
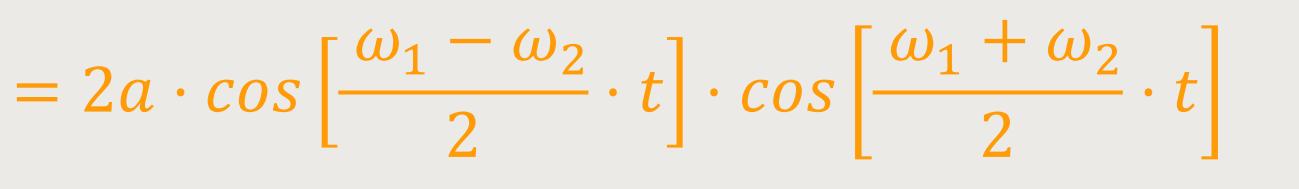
Und wie lässt sich das jetzt interpretieren?

­

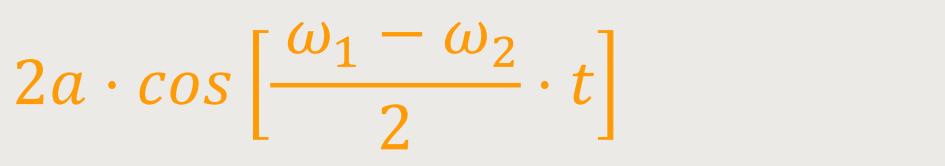
... ist eine Amplitude mit langsamer periodischer Änderung
wogegen

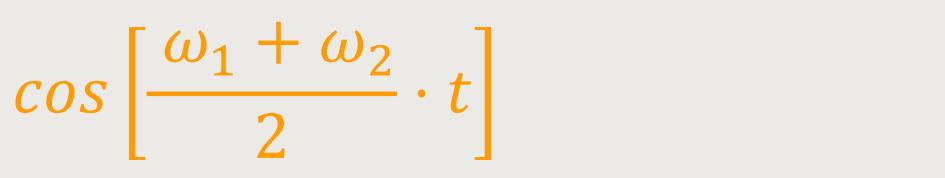
... ist der arithmetische Mittelwert der beiden Frequenzen.

Als nächstes betrachten wir mehrere Schwingungen mit unter­schied­lichen Frequenzen.

Vorerst wird dieser Bereich inhaltlich nur gestreift. Es ist zwar ein wichtiges Gebiet, aber wegen seiner Komplexi­tät können wir nur kurz darauf eingehen.

Wenn man Schwingungen mit unter­schied­lichen Frequenzen über­lagert, sodass mit zuneh­mender Frequenz bei gleichen Phasen­lagen die Amplituden immer kleiner gewählt werden, und man anschließend alle addiert, ergibt sich ein spezi­fisches Schwingungs­bild. Zum Teil gleichen diese Schwingungs­bilder einem Sägezahnmuster.

Das heißt, man kann unter­schied­liche nicht harmonische aber periodische Schwingungs­vorgänge dadurch darstellen, dass man sie sich zusammen­gesetzt denkt. Und das führt zu den in der Mathe­matik sehr gut unter­suchten Fourier-Reihen. Es lassen sich nämlich verschiedene periodische Funktionen in sehr all­gemeiner Weise durch Fourier-Reihen darstellen, wodurch diese mit immer besser werdender Näherung durch viele harmonische Schwingungen visualisiert werden können.

Das ist zum Beispiel in der Akustik der Fall. Dort spricht man davon, dass solche Schwingungen, die nicht unbedingt nur harmonisch sind, durch Obertöne charakte­risiert werden. Das sind Töne mit höheren Frequenzen, die aber eine geringere Amplitude haben.

Insofern kann man durch die verschie­denen Schwingungen eine Fourier-Analyse durch­führen. Eine beliebige und oft komplizierte Schwingungs­form lässt sich letzt­lich dar­stellen, als das Ergebnis einer Rein­entwicklung mit zunehmenden Frequenzen und immer kleineren Amplituden.

Als Nächstes werden wir eine weitere Verallge­meinerung betrachten. Und zwar den Fall, dass zwei Schwingungen vor­handen sind, die nicht auf der gleichen Achse liegen, sondern Schwingungen bei denen die eine Schwingung und die andere Schwingung unter 90° zueinander ver­laufen. Derartige Schwingungen „in der Ebene” haben den interes­santen Aspekt, dass solche Über­lagerungen 2-dimensional sind.

Jetzt haben wir also die Situation, dass eine Schwingung in der x-Richtung verläuft und eine andere in der y-Richtung. Die Summe der beiden führt dann zu einer Bewegung bzw. Über­lagerung in dieser 2-dimen­sionalen Ebene. Die Betrachtungs­weise darf jedoch nicht mit dem Zeiger­diagramm verwechselt werden. Wir haben jetzt nicht mehr die komplexe Ebene.

Für zwei senkrecht aufeinander liegende Schwingungen mit gleicher Frequenz ergibt sich:

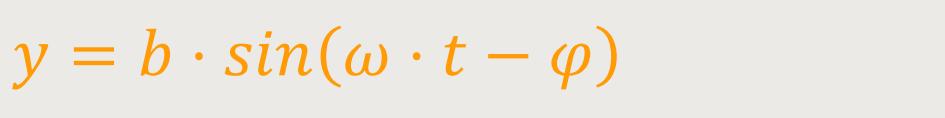
a, b   sind die Amplituden
φ     ist die Phasen­verschiebung

Durch die Über­lagerung der Schwingungen erhält man eine Kurve, die in einer 2-dimen­sionalen Ebene durch­laufen wird. Um zu einer Gleichung für diese Kurve zu kommen, muss man aus diesen beiden Gleichungen die Zeit t eliminieren. Nach mehreren Umformungen kommt man letzten Endes auf folgende Gleichung:

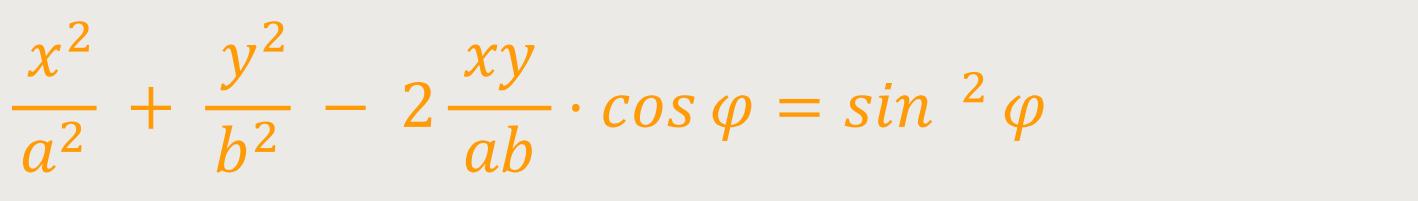
Das Ergebnis ähnelt stark einer Ellipsen­gleichung, die sich wie folgt beschreiben lässt:

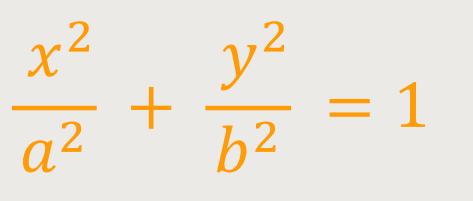
Wir haben ja eine Schwingung entlang der x-Achse und eine Schwingung entlang der y-Achse. Wenn man beide Schwingungen über­lagert, entsteht eine Kreis­frequenz. Aber mit dem zusätz­lichen Term in der vor­herigen Gleichung kann es auch passieren, dass sich der Kreis zu einer oszillierenden Ellipse ausbildet. Das wird insbe­sondere durch die unter­schiedliche Phasen­verschiebung hervorgerufen.

Man kann aber auch Schwingungen in zwei Dimensionen mit einem „rationalen Frequenz­verhältnis” betrachten. Die Rechnungen sind dann zwar etwas komplizierter, aber je nach Phasen­lage kommen trotz­dem geschlossene Bahn­kurven heraus.

Wenn man das Ergebnis mittels Oszillator visualisiert, erhält man die soge­nannten Lissajous-Figuren. Interes­santer Weise lassen sich diese Figuren auch mit einem mecha­nischen Experiment zeigen.

Aber die Frequenz­verhältnisse können durch­aus auch irrational sein.

Bei „irrationalem Frequenz­verhältnis” gibt es keine ein­heit­liche Kurve mehr. Die Kurven werden mit ständig wechselnden Phasen­lagen immer wieder neu durch­laufen. Am Oszillator wird letzten Endes ein Recht­eck als Grafik ganz aus­gefüllt sein.

Vor allem wenn man große Frequenz­verhält­nisse hat, ist anschlie­ßend die ganze Fläche gleich­mäßig über­strichen. Die Bahn­kurve geht immer wieder über neue Teile der Fläche und dadurch erhält man eine gleich­mäßige Über­lagerung der ganzen recht­eckigen Fläche mit den beiden Amplituden.

Das hat nichts mehr mit den Lissajous-Figuren zu tun.

⇦ Kapitel Kapitel ⇨