Die nächste Art von Schwingungen, die wir betrachten, sind die „erzwungenen Schwingungen”. Bei einem Oszillator kommt es näm­lich auch darauf an, wie man ihn über­haupt in Schwingung versetzt. In vielen Fällen ist es so, dass eine äußere periodische Kraft auf einen der­artigen Oszillator wirkt.

Wobei diese äußere perio­dische Kraft eine bestimmte von außen vorge­gebene zeit­liche Periode hat. Also, eine Frequenz bzw. eine Kreis­frequenz. Und dann gilt es zu unter­suchen, wie der Oszillator auf diese äußere perio­dische Kraft reagiert.

In diesem Zusammen­hang schaut man sich wieder die Bewegungs­gleichung an, zunächst durch Auf­stellen einer Differential­gleichung:

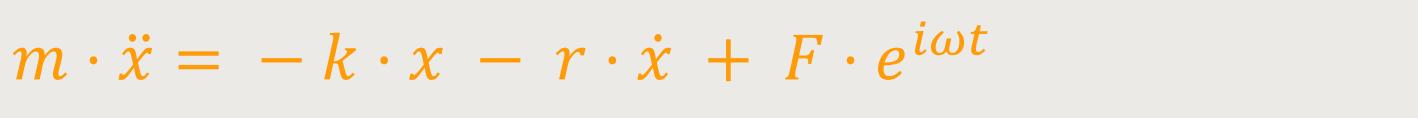
k   ist die Rückstell­konstante
r   ist die Reibungskonstante
F   ist die Amplitude der äußeren Kraft
ω   ist die Kreisfrequenz der äußeren Kraft

Durch Umformung kann man auch schreiben:

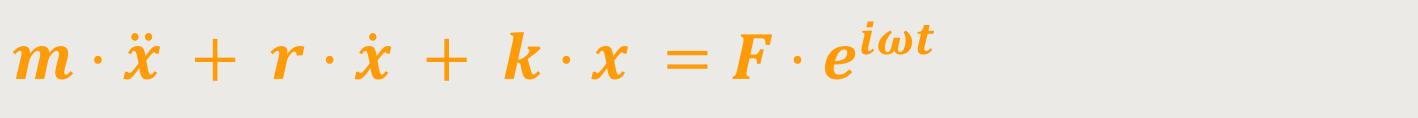
Das ist jetzt die Differential­gleichung für die erzwungenen Schwingungen eines harmonischen Oszillators.

Die Kreis­frequenz wird in diesem Fall erzwungen bzw. vorgegeben. Dies kann zum Beispiel während eines Versuchs­aufbaus durch einen Motor geschehen. Wenn die äußere Frequenz jedoch so ein­geregelt wird, dass man sich der Eigen­frequenz des Oszillators nähert, kommt es zu einer soge­nannten „Resonanz­katastrophe”. Der­artige Vorfälle kann man bei ungünstig auf­einander folgenden Windböen oder Erdbeben beobachten.

Dementspre­chend erhält man die Eigen­frequenz für einen ungedämpften Oszillators:

Aber so wird im Allge­meinen der Oszillator in der Realität nicht schwingen, weil es eben diese von außen wirkende Kraft gibt. Um in unserer Über­legung bezüg­lich der erzwungenen Schwingungen weiter zu kommen, muss man wieder einen komplexen Lösungs­ansatz machen:

Doch jetzt muss man wachsam sein. Die Kreis­frequenz ω ist hier vorge­geben durch die äußere Kraft. Es gibt nun einen Unter­schied in der grund­sätz­lichen Ein­stellung. Die all­gemeine Lösung der inhomogenen Differential­gleichung setzt sich näm­lich aus zwei Kompo­nenten zusammen. Zum einen additiv aus der allge­meinen Lösung der homogenen Gleichung, plus einer speziellen Lösung der inhomogenen Gleichung.

Die allgemeine Lösung der homogenen Gleichung klingt mit der Zeit­konstante τ (tau) ab. Nach einer gewissen Zeit ist diese Gleichung gar nicht mehr spürbar, wenn man eine entspre­chende Dämpfung hat. Was bleibt, ist ein stationärer Schwingungs­vorgang unter dem Einfluss der äußeren Kraft.

Wenn man sich das entspre­chend ausrechnet, bleibt im Wesent­lichen wieder eine quadratische Gleichung. Aber diesmal nicht für die Kreis­frequenz ω, wie bei der normalen Schwingung, sondern eine quadra­tische Gleichung für die Amplitude a.

Wie schaut der Betrag dieser Amplitude aus? Diese Amplitude ist auch eine komplexe Zahl.

Und man erhält als Ergebnis: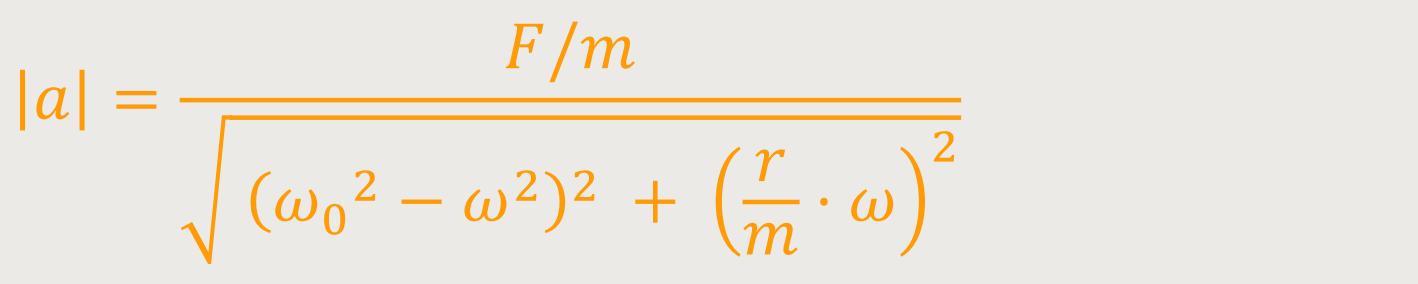

m   ist die Masse des schwingenden Körpers

Dieser Ausdruck für den Betrag der Amplitude ist in der komplexen Ebene der Abstand vom Ursprung. Man hat damit die Amplitude der betrachteten Schwingung im stationären Zustand. Und was ergibt sich daraus?

Wenn die Dämpfung nicht zu groß ist, dann wird der zweite Term in der Wurzel klein sein. Und wenn die äußere Anregung in die Nähe der Eigen­frequenz des ungedämpften Oszillators kommt, dann wird der Nenner im ersten Term in der Wurzel sehr klein. Ist aller­dings die äußere Anregung gleich dem ω_₀, dann fällt dieser erste Term ganz weg.

Übrig bleibt bei kleiner Dämpfung nur ein einziger kleiner Term, und zwar der zweite Term im Nenner. Ein kleiner Nenner bedeutet eine große Amplitude, und das kann dann soweit gehen, dass es zu dieser Resonanz­katastrophe kommt.

Die Breite der soge­nannten Resonanz hängt von der Dämpfung ab, die in dem Oszillator vor­handen ist. Je stärker der Oszillator gedämpft ist, desto breiter wird das Maximum der Amplituden werden. Dieses Verhalten, nämlich dass der Oszillator optimal schwingt, wenn er in der Nähe seiner Eigen­frequenz angeregt wird, ist die soge­nannte „Resonanz”. Und Resonanzen sind in der Physik in vielen Bereichen etwas außer­ordent­lich Wichtiges.

Was ist aber, wenn man die Dämpfung noch kleiner machen würde, wenn die Dämpfung quasi gleich Null ist? Dann wird der ganze Nenner Null. Als Konsequenz daraus wird die Amplitude unendlich groß, und sie schaukelt sich mehr und mehr auf. Es wird durch die äußere Kraft immer mehr Energie in das System „hinein­gepumpt” und die Reibung ist nicht mehr in der Lage, die Energie abzu­führen und letzten Endes in Wärme umzu­setzen. Schließ­lich kommt es zur Resonanz­katastrophe. Bei Annähe­rung an die Eigen­frequenz ω_₀ wächst die Amplitude über alle Grenzen.

Die quadratische Gleichung für die Amplitude a ist nur solange sinn­voll, solange das r groß genug ist, damit dieser Fall der Resonanz­katastrophe nicht eintritt. Und das hat auch sehr wichtige prak­tische Konse­quenzen. Denn in vielen Fällen ist es so, dass schwingungs­fähige Systeme wie zum Beispiel Brücken durch äußere Kräfte zu Schwingungen angeregt werden.

Schwingungen finden immer nur an einem stationären Ort statt, so wie ein lokaler Oszillator mit seinen Schwingungs­eigenschaften. Er hat also nur eine zeit­liche Periodi­zität. Wellen dagegen haben zusätz­lich zur zeit­lichen Kompo­nente noch eine räumliche Kompo­nente. Damit sich der­artige Schwingungen aus­breiten können, muss man mehrere Oszillatoren betrachten, die mit­einander gekoppelt sind.

Solche „gekoppelten Schwingungen” von mehreren Oszillatoren, sind relativ kompliziert zu beschreiben. Man erhält dann einen Satz von mehreren gekoppelten Differential­gleichungen, die gemeinsam gelöst werden müssen. Das sind dann mehrere Lösungs­funktionen, die den jeweiligen Aus­lenkungen in den verschiedenen gekoppelten Oszillatoren entsprechen.

Wie kann man sich solche gekoppelten Schwingungen vorstellen?

Hierzu stellt man sich gedank­lich einen doppelten Spiral­feder-Oszillator vor, bei dem zwei Massenpunkte durch drei Spiral­federn räum­lich von­einander getrennt sind und in horizontaler Lage zwischen zwei seit­lichen Wänden positioniert sind. Man hat dann zwei Oszillatoren, die sich zunächst in einer Gleich­gewichts­lage befinden. Wenn einer der beiden Oszillatoren in Schwingung versetzt wird, wird er über die Koppelungs­feder den anderen Oszillator eben­falls anregen.

Dann wird sich die erste Schwingung auf den zweiten Oszillator über­tragen. Wenn man sich das jetzt für eine Viel­zahl von gekoppelten Oszillatoren vorstellt, wird sich so ein Schwingungs­vorgang im Laufe der Zeit räum­lich aus­breiten. Das führt dann von einem einzelnen Oszillator auf ein Wellenfeld. Neben den beiden Rück­stell­konstanten k_₁ und k_₂ der Spiral­federn, gibt es zwischen den Massen noch eine Koppelungs­konstante k_{₁ ₂}, die dafür sorgt, dass die beiden Oszillatoren mit ihren Rück­stell­konstanten noch mit­einander verkoppelt sind.

Wenn man beispiels­weise bei zwei gekoppelten Oszillatoren, den einen in Schwingung versetzt, beginnt der zweite zunächst langsam und dann immer stärker mitzu­schwingen. Der zweite Oszillator wird damit einen Teil der Energie des ersten Oszillators über­nehmen. Bis der zweite schließ­lich die gesamte Energie des ersten über­nommen hat.

Betrachtet man hierzu ein symme­trisches System, schwingt die Schwingungs­energie perio­disch zwischen den beiden Massen­punkten hin und her. Das ent­spricht quasi einer Reflexion zwischen diesen beiden gekoppelten Oszillatoren.

Und das ist jetzt der Ausgangs­punkt, von den Schwingungen auf die Wellen über­zugehen.

⇦ Kapitel Kapitel ⇨