Licht und andere elektro­magnetische Wellen sind Wellen ohne Medium. Da gibt es nichts, was schwingt. Wir sprechen hier vorerst nur über mecha­nische Wellen, also Wellen mit einem Medium.

Zu den unter­schied­lichen Wellen­arten gehören die trans­versalen und longi­tudinalen Wellen. Eine trans­versale Welle ist das, was man allge­meinhin kennt. Die Aus­lenkungen erfolgen quer zur Ausbreitungs­richtung.

Sehr geläufig sind auch die Schall­wellen. Da erfolgt die Auslenkung aller­dings in Ausbreitungs­richtung. Deshalb handelt es hierbei um eine longi­tudinale Welle. In flüssigen oder gasförmigen Medien können die Wellen nicht transversal verlaufen, weil in Flüssig­keiten und Gasen die Scher­wirkungen keine Rolle spielen.

Vielleicht erinnern wir uns an die Elastizitätslehre. In Verbindung mit den Fluiden gab es nur einen Parameter, nämlich die Kompressi­bilität. Das Thema Scherung tritt dagegen nur bei Fest­körpern auf. Insofern können Fest­körper trans­versal schwingen. Aber auch, und das würde man womög­lich nicht vermuten, verlaufen die elektro­magnetischen Wellen auch transversal.

Fluide können somit nur longitudinal schwingen. Die Auslenkung und die Ausbreitungs­richtung der einzelnen Oszillatoren erfolgen immer in der gleichen Richtung. Dadurch kommt es in den Fluiden zu Verdich­tungen und Verdün­nungen. Das führt wiederum zu höheren und niedrigeren Druck­verhält­nissen.

Schall­wellen sind beispiels­weise einfach nur Druck­schwan­kungen mit entspre­chenden Frequenzen und einem Frequenz­spektrum. Letzten Endes ist das eine Folge von Druck­schwan­kungen bzw. periodischen Druck­stößen, die sich in der Luft aus­breiten und deshalb das Trommel­fell in Bewegung ver­setzten. Das ist das Prinzip bei den Longi­tudinal­wellen.

Jetzt wollen wir aber doch noch einen Ansatz betrachten, der dazu dienen kann, solche Wellen darzu­stellen. Und zwar mit Hilfe einer Auslenkungs­funktion. Auch hier betrachten wir die Wellen nur 1-dimen­sional in der x-Richtung.

Hinweis: Exponential­funktionen lassen sich viel besser differen­zieren, als einen Sinus oder einen Kosinus (Cosinus). Aber hier wird eine solche Funktion nicht benötigt.

Deshalb schreibt man den Kosinus als Realteil des komplexen Ansatzes, und so ergibt sich:

Das ist der (reelle) Ansatz für die Wellen­ausbreitung.

u   ist die momentane Auslenkung als Auslenkungs­funktion
u_₀   ist die Amplitude (maximale Auslenkung)
ω   ist nach wie vor die Kreisfrequenz
k   ist die sogenannte Wellenzahl

Die Auslenkung hat zum einen eine Zeit­abhängig­keit (seitlich) aber auch eine Orts­abhängig­keit (in Laufrichtung). Beide Abhängig­keiten sind harmonische Abhängig­keiten, was man am Kosinus (Cosinus) erkennen kann. Wie kann man sich vorstellen?

Nehmen wir an, wir konzen­trieren uns auf einen bestimmten Orts­punkt. Wenn jetzt eine Aus­lenkung der Schwingung erfolgt, sieht man ein auf und ab dieser Aus­lenkung, die periodisch mit der Zeit erfolgt. Würde man in der Gleichung x = 0 ein­setzen, bleibt nur noch ein cos (ωt). Dann hätte man an der Stelle x = 0 einen Oszillator der so schwingt, wie wir das bisher schon betrachtet haben.

Anderer­seits, wenn man eine Moment­aufnahme machen würde, dann wäre die Abhängig­keit (x) periodisch. Aber durch die Moment­aufnahme wäre in diesem Fall auch t = 0, und dann bliebe nur cos (−k · x) übrig. In diesem Fall ist auch die Abhängig­keit (x) periodisch. Das Argument des Kosinus kann man deshalb als Phase bezeichnen.

Mit der Kreis­frequenz ergibt sich wieder die Schwingungs­dauer an jedem einzelnen individuellen Punkt:

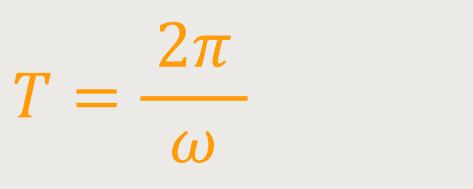
Und für die Frequenz gilt:

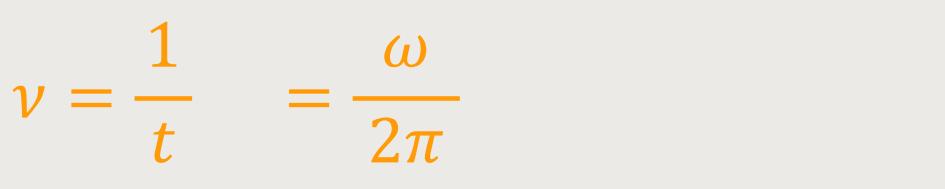
Das entspricht in ähn­licher Weise der Anzahl der Schwingungen pro Zeit­einheit. Beides hatten wir schon in Verbindung mit den all­gemeinen Schwingungen. Und jetzt zeigt sich in völlig analoger Form, indem man sich zu irgend­einem frei wählbaren Zeit­punkt t = 0 die räum­liche Abhängig­keit anschaut.

So wie die Schwingungs­dauer jeweils angibt, wie groß der zeit­liche Abstand zwischen zwei homologen Punkten der Schwingung ist, so gibt es auch bei der räum­lichen Aus­breitung einen Abstand von homologen Punkten. Und das nennt man dann die Wellen­länge:

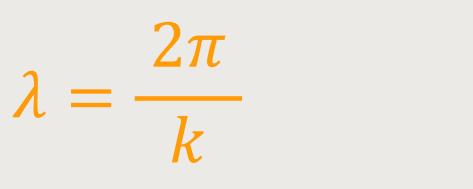
Wir erhalten damit eine Größe, die ähnlich anschau­lich ist, wie die Schwingungs­dauer. Es ist der Abstand zwischen zwei Wellen­bergen. Die Anzahl der Wellen pro Längen­einheit ist dann:

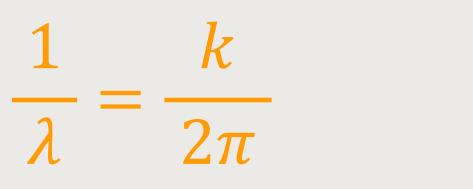
An jedem Punkt in einem Wellen­feld gibt es einen Oszillator, der eine harmonische Schwingung durch­führt.

Sowohl bei einer Schwingung als auch bei einer Welle, ist die Phase das Argument der entspre­chenden perio­dischen Funktion. Entweder bei der komplexen e-Potenz oder wie hier bei der Kosinus­funktion. Und diese Phase ist dann auch ent­scheidend dafür, wie sich die Schwingung dar­stellt. Wenn zum Beispiel die Phase zu einem bestimmten Zeit­punkt an einem bestimmten Ort Null ist, dann ist der Kosinus von 0 = 1. Das heißt, dann wird diese Aus­lenkung u den maxi­malen Wert u_₀ annehmen. Das nächste Mal wieder­holt sich das entspre­chend, wenn die Phase 2π durch­laufen hat.

Mit anderen Worten, wenn die Phase den Wert Null annimmt, befindet man sich während der Schwingung bei einem Wellen­berg, also an der Stelle, wo die Aus­lenkung positiv maximal wird. Das bedeutet im Fall einer sich räum­lich aus­brei­tenden Welle, dass sich dieser Wellen­berg aus­breitet. Das gleiche gilt für ein Wellen­tal oder irgend­einen anderen festen Punkt.

Nach Möglich­keit möchte man eine Infor­mation darüber erhalten, wie schnell sich diese Welle im Raum aus­breitet. Diesen Aspekt gab es bei den Schwingungen noch nicht, weil es bei den Schwingungen ja keine räum­liche Aus­breitung gab. Da hatten wir uns nur einen Oszillator angeschaut. Jetzt betrachten wir aber viele Oszillatoren, die alle mit­einander verkoppelt sind.

Das führt zwangs­läufig zu einer Aus­breitung der Schwingung. Wie schnell das vonstatten­geht, hängt im Wesent­lichen damit zusammen, wie schnell sich diese Wellen­berge oder Wellen­täler aus­breiten. Also, wie schnell sich Punkte konstanter Phase ausbreiten.

Diese Definition für die Ausbreitungs­geschwin­dig­keit führt auf den Begriff der soge­nannten Phasen­geschwindigkeit.

Hierzu schaut man sich dieses ωt −k · x aus obiger Bewegungs­gleichung an, leitet es nach der Zeit ab und setzt es Null.

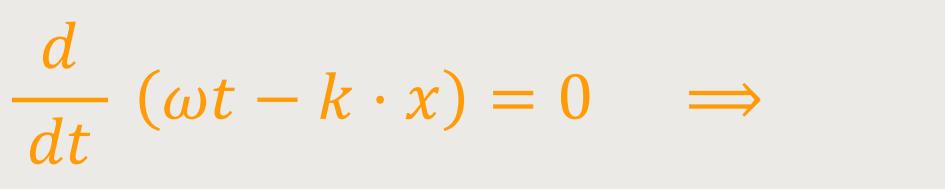
Wenn man das so auf­schreibt, verlangt man nach Punkten konstanter Phase. Nun kann man das wieder differenzieren:

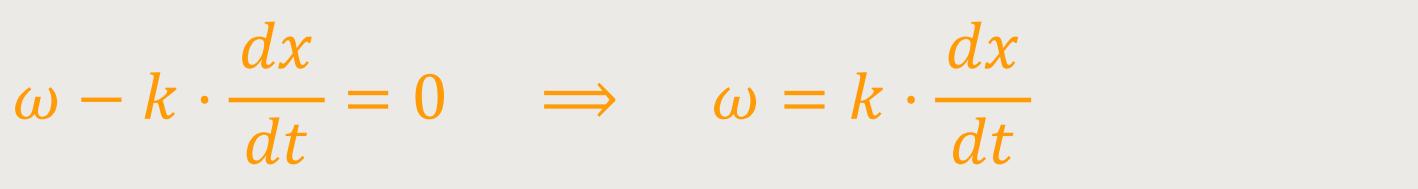
dx /dt   ist die Phasen­geschwindigkeit v_ph

Durch Einsetzen erhält man:

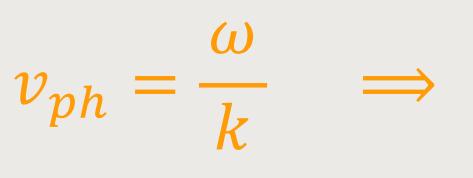
Wie hängt nun die Kreis­frequenz ω und die Wellen­zahl k mit der Schwingungs­dauer und der Wellen­länge zusammen?

Bei der Schwingungs­dauer haben wir bereits betrachtet, dass die Schwingungs­dauer umgekehrt propor­tional zur Frequenz ist. Je kleiner die Schwingungs­dauer, desto mehr Schwingungen ergeben sich pro Sekunde.

Folgender Ausdruck beschreibt die Phasen­geschwindigkeit:

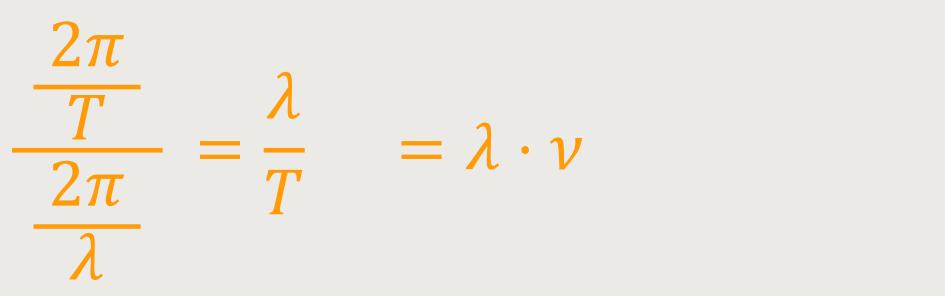
λ   ist die Länge eines Wellenzuges im Raum
ν (nu)   ist die Anzahl der Schwingungen pro Zeiteinheit

Wenn eine Schwingung aus­gelenkt wird, dann wird entspre­chend eine Wellen­länge durch­laufen. In der Zeit, wo eine Schwingung abge­schlossen ist, durch­läuft eine Wellen­länge den Raum. Daher werden pro Zeit­einheit ν-mal solche Wellen­längen weiter­getragen.

So einfach wie das im Moment aussieht, ist es aber nicht. Denn bis jetzt haben wir nur eine andauernd gleich­mäßig schwingende Quelle, bei der solche Wellen erzeugt werden. Natür­lich kann man betrachten, wie sich die Wellen­berge mit der Phasen­geschwindig­keit fort­bewegen. Wenn aber mit Hilfe einer Welle Infor­mationen über­mittelt werden sollen, reicht es nicht aus, eine Licht­quelle einmal einzu­schalten und dann leuchten zu lassen.

Möchte man beispiels­weise Morse­zeichen über­tragen oder irgend­welche anderen Infor­mationen, muss diese Welle verändert werden. Um das zu bewerk­stelligen, muss ein Impuls ausge­sendet werden. Und durch mehrere Impulse gelingt es dann schließ­lich, Informa­tionen zu über­tragen. Insofern kann eine gleich­mäßige unver­änder­liche Wellen­aus­breitung am anderen Ende keine Infor­mation über­tragen.

Es geht also immer um die alles entschei­dende Frage, wie man Infor­mationen übertragen kann. Und das geschieht typischer­weise nicht mit einer gleich­mäßig sich aus­breitenden harmonischen Welle, sondern mittels Wellen­gruppen bzw. Wellen­paketen.

Ein „Wellenpaket” ist im Wesent­lichen ein Impuls, der ausge­sendet wird. Das Besondere dabei ist, dass sich der Impuls nicht mit der Phasen­geschwindig­keit ausbreitet. Die Ausbreitungs­geschwindig­keit von der­artigen Wellen­paketen ist in der Regel unter­schied­lich. Womit hängt das zusammen?

Es gibt bei den Wellen­paketen eine soge­nannte Umhüllende oder „Einhüllende”. Die Geschwindig­keit, mit der sich so ein Wellen­paket ausbreitet, ist dann im Wesent­lichen die Geschwindig­keit, mit der sich das Maximum dieser Einhül­lenden bewegt. Das nennt man auch die „Gruppen­geschwindig­keit”. Wie lässt sich diese Gruppen­geschwindig­keit darstellen?

Man kann hierbei eine ähnliche Über­legung anstellen, wie wir das bereits bei den Über­lagerungen von Schwingungen betrachtet haben. Das gleiche Prinzip kann man beobachten, wenn sich zwei Wellen mit gering­fügig unter­schied­lichen Wellen­längen in der gleichen Richtung aus­breiten. Es ergibt sich eine ganz ähnliche Situation des „Schwebens”, nur diesmal im Raum. Dadurch ergibt sich ein räum­licher Fischzug, von aneinander gelagerten einzelnen Wellen­paketen.

Am besten lassen sich solche Wellen­pakete dar­stellen, wenn man nicht nur eines für sich allein betrachtet, sondern eine ganze Anzahl von Wellen­paketen hinter­einander. Das lässt sich mit zwei harmo­nischen Wellen reali­sieren, die sich beide längs der x-Achse (1-dimen­sional), mit jeweils gering­fügig unter­schied­lichen Wellen­längen aus­breiten. Die beiden Wellen kommen im Laufe der Zeit immer wieder ein bisschen aus der Phase. Aber wie schnell werden sich die dadurch ergebenden einzelnen Wellen­pakete ausbreiten?

Dazu muss man die gemein­same Verstärkung dieser beiden Wellen­pakete betrachten. Das heißt, eine Verstärkung wird dann auf­treten, wenn sich die entspre­chenden Phasen der beiden über­lagern. Dann hat man quasi ein gemein­sames Maximum der Einhül­lenden. Es geht darum, wie rasch sich die­jenigen Punkte aus­breiten, bei denen diese Verstär­kung auf­grund der Über­ein­stimmung der Phasen auftritt.

In diesem Fall ergibt sich auf der linken Seite (der Gleichung) die Phase der einen Welle:

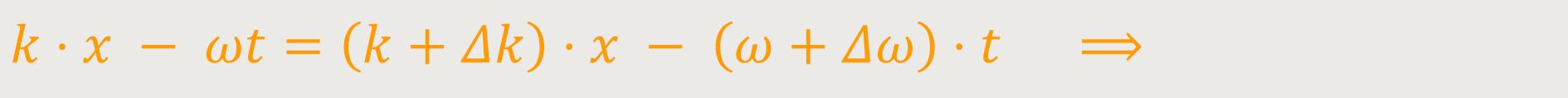
Die zweite Welle auf der rechten Seite (der Gleichung) hat demnach eine leicht unter­schied­liche Wellen­zahl mit einer leicht unter­schied­lichen Kreis­frequenz. Nach dem Wegkürzen bleibt nur mehr stehen:

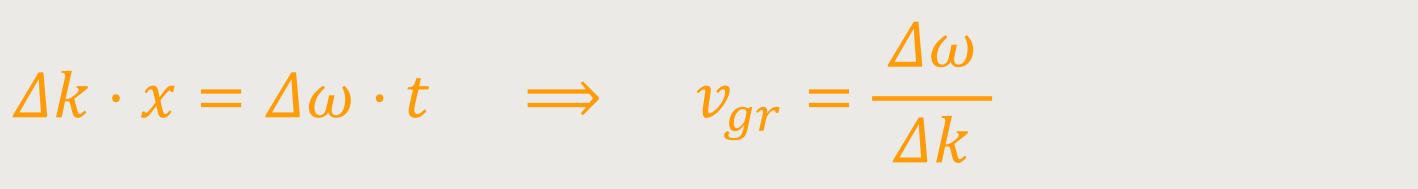
x /t = v_gr   ist die Gruppen­geschwindigkeit

Und so kommt man letzten Endes zu dem Ergebnis, dass die Aus­breitung eines einzelnen Wellen­pakets, welches sich in diesem Fall darstellen lässt, durch die Über­lagerung zweier solcher Wellen, quasi einer Gruppe, geschrieben werden kann als:

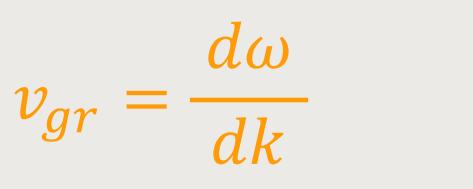
Wenn man jetzt den Grenz­wert von sehr kleinen Unter­schieden bildet, ist das der Differential­quotient.

Es besteht eine Ähnlich­keit zwischen der Phasen­geschwindig­keit und der Gruppen­geschwindig­keit. Insofern ergibt sich die Frage, wie hängt jetzt die Gruppen­geschwindig­keit mit der Phasen­geschwindig­keit zusammen?

Mit Bezug auf die Phasengeschwindigkeit gilt zunächst:

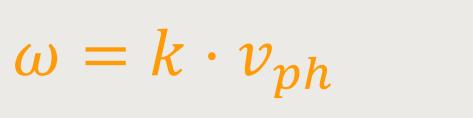
Wenn man das in der Gleichung für die Gruppen­geschwindig­keit einsetzt, ergibt sich:

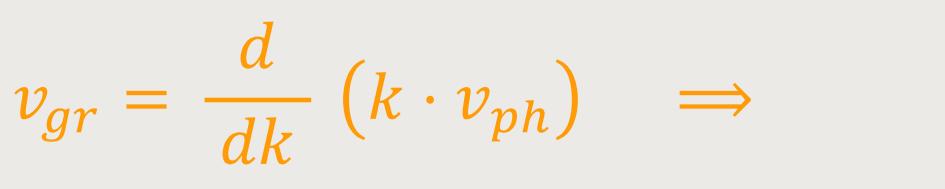
Wenn man diesen Ausdruck differenziert, erhält man:

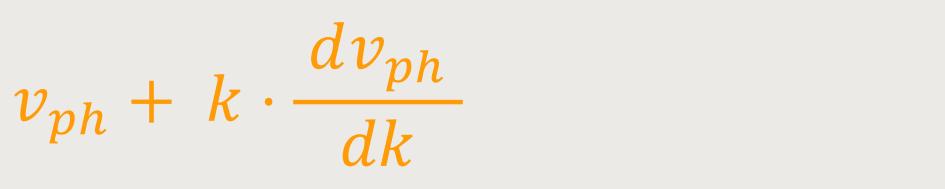
Jetzt mag man sich fragen, ist die Phasen­geschwindig­keit nicht etwas konstantes, dann wäre sie doch eh Null.

Das ist im Allge­meinen aber nicht der Fall. Weil die Phasen­geschwindig­keit von Punkten konstanter Phase immer davon anhängt, wie die einzelnen gekoppelten Oszillatoren mit­einander wechsel­wirken. Diese Wechsel­wirkung kann mit der Frequenz und somit mit der Wellen­länge zusammen­hängen, und sich entspre­chend ändern. Das heißt, im Allgemeinen muss man davon ausgehen, dass die Phasen­geschwindig­keit von der Wellen­zahl k und damit von der Wellen­länge abhängig ist.

Das zeigt sich auch in der Praxis. Zum Beispiel ist der Brechungs­index, der ja mit der Phasen­geschwindig­keit des Lichts zu tun hat, abhängig von der Farbe des Lichts, also abhängig von der Wellen­länge. Die Dispersion des Lichts in verschiedene Farben hat letzt­lich die Ursache darin, dass das Licht seine Ausbreitungs­geschwindigkeit ändert. Je nachdem wie sich die Wellen­länge in einem entspre­chenden Medium ändert.

Also, das dv_ph /dk wird im Allge­meinen nicht gleich Null sein. Dabei gilt zu berück­sichtigten, wie die Wellen­zahl k mit der Länge eines Wellen­zuges λ zusammen­hängt:

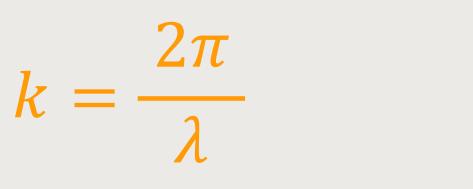
Wenn man jetzt die Gleichung der Phasen­geschwindig­keit entspre­chend umformt, dann folgt daraus:

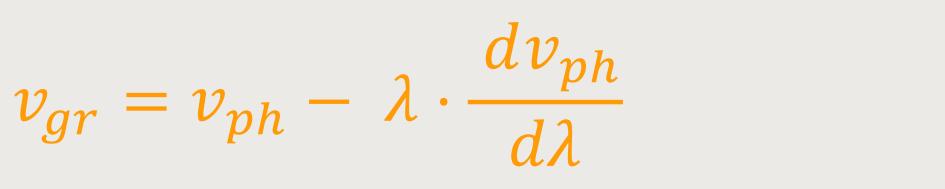
Dieses Ergebnis ist relativ einfach physika­lisch zu inter­pretieren. Der Term dv_ph /dλ beschreibt die Abhän­gig­keit der Phasen­geschwindig­keit der betrach­teten Welle von der Wellen­länge. So wie es zum Beispiel bei der Aus­breitung des Lichts in durch­sichtigen Medien (Glas) der Fall ist, indem dort die Aus­breitungs­geschwindig­keit dieser Licht­wellen von der Frequenz und von der Wellen­länge abhängt.

Wenn also die Phasen­geschwindig­keit von der Wellen­länge abhängig ist, dann spricht man auch davon, dass „Dispersion” vor­liegt. Und wenn Dispersion vor­liegt, dann unter­scheidet sich die Gruppen­geschwindig­keit von der Phasen­geschwindig­keit. Im Allge­meinen wird dann die Gruppen­geschwindig­keit lang­samer sein als die Phasen­geschwindig­keit.

Im Fall des Lichts kann die Phasen­geschwindig­keit sogar größer sein als die Vakuum­licht­geschwindig­keit. Aller­dings kann mit der Phasen­geschwindig­keit keine Information über­tragen werden. Insofern wird die Gruppen­geschwindig­keit entspre­chend geringer sein, und stets unter der Vakuum­licht­geschwindig­keit liegen.

Es gibt also einen Unter­schied zwischen der Aus­breitung der Punkte konstanter Phase und der Aus­breitung von einzelnen Wellen­paketen, die man durch Über­lagerung einer Gruppe einzelner Wellen dar­stellen kann. Und wenn man ein Wellen­paket betrachtet, dann wird sich das mit der gleichen Geschwindig­keit aus­breiten, falls die Phasen­geschwindig­keit nicht von der Wellen­länge abhängt.

Nehmen wir noch­mals das Licht. Wenn es sich im Vakuum ausbreitet, gibt es keine Dispersion. Licht und all­gemein elektro­magne­tische Wellen breiten sich im Vakuum immer mit der Vakuum­licht­geschwindig­keit aus. Das ist etwas Unveränder­liches. Wenn man eine Licht­welle im Vakuum ausbreiten lässt, viel­leicht sogar in Form von Wellen­gruppen, werden sich diese Pakete auch mit der Vakuum­licht­geschwindig­keit aus­breiten. Das ist so, weil das Licht im Vakuum eben keine Dispersion zeigt.

Wenn man hingegen Licht durch ein durch­sichtiges Medium laufen lässt, dann ist die Licht­geschwindig­keit dort sehr wohl von der Wechsel­wirkung mit den Molekülen in diesem Medium abhängig. Und dem­entspre­chend wird die Phasen­geschwindig­keit von der Wellen­länge abhängig sein. Das ist genau das, was man all­gemein als Dispersion bezeichnet. Und das führt auch letzt­lich dazu, dass wenn weißes Licht durch ein Glas­prisma hin­durch tritt, dieses weiße Licht dispergiert wird. Und zwar in die einzelnen Farben aus denen es zusammen­gesetzt ist.

Also, falls Dispersion vorliegt, unter­scheidet sich die Gruppen­geschwindig­keit von der Phasen­geschwindig­keit.

⇦ Kapitel Kapitel ⇨