In den Bereichen Mathematik und Physik entspricht ein n-dimen­sionaler De-Sitter-Raum (nach Willem de Sitter), der mit dS_n notiert ist, der Lorentz'schen Mannig­faltig­keit, analog zu einer n-Sphäre. Diese Sphäre beinhaltet die kanonische Riemann'sche Mannig­faltig­keit. Der De-Sitter-Raum ist maximal symmetrisch, hat eine konstante positive Krümmung und ist ein­fach zusammen­hängend für n ≥ 1.

Im 4-dimen­sionalen Minkowski-Raum, den wir zuvor betrachtet haben (3 Raum­dimensionen plus die Zeit), man könnte auch all­gemein von der „Raumzeit” sprechen, ist der De-Sitter-Raum das Analogon zu einer Kugel im euklidischen Raum.

In der Sprache der Allgemeinen Relativitätstheorie (ART) ist der De-Sitter-Raum die maximal symmetrische Vakuum­lösung der einsteinschen Feldgleichungen mit einer positiven (repulsiven) kosmolo­gischen Konstanten Λ (entspre­chend einer positiven Vakuum­energie­dichte und negativem Druck) und damit ein kosmolo­gisches Modell für das physika­lische Universum. Der De-Sitter-Raum wurde 1917 von Willem de Sitter entdeckt und parallel von Tullio Levi-Civita.

Der De-Sitter-Raum kann definiert werden als Unter­mannig­faltig­keit eines Minkowski-Raumes einer höheren Dimension.

Betrachtet man also den Minkowski-Raum R^{1, n} mit dem üblichen metrischen Tensor:

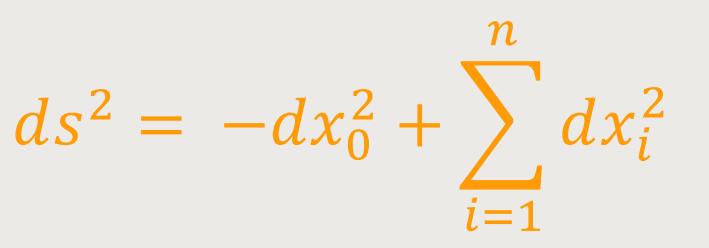
... dann ist der De-Sitter-Raum die Unter­mannig­faltig­keit, die durch das einschalige Hyperboloid

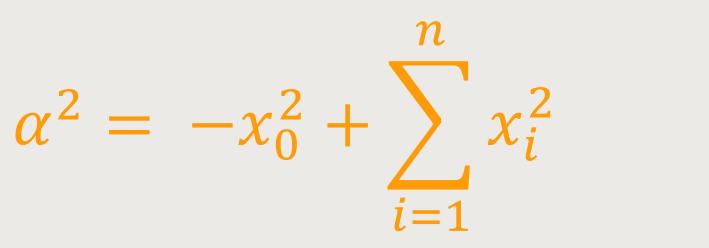
... beschrieben wird, wobei α eine positive Konstante mit der Dimension einer Länge ist. Der metrische Tensor des De-Sitter-Raumes ist derjenige, der vom metrischen Tensor des Minkowski-Raumes erzeugt wird. Man kann über­prüfen, dass die erzeugte Metrik nicht entartet ist und eine Signatur der Form (1, k, 0) hat.

Wenn in obiger Definition α² durch −α² ersetzt wird, erhält man ein zwei­schaliges Hyper­boloid. In diesem Fall ist die erzeugte Metrik positiv definiert, und jede der beiden Schalen ist eine Kopie einer hyperbo­lischen n-Geometrie.

Abb. 1: 2-dimensionaler De-Sitter-Raum.
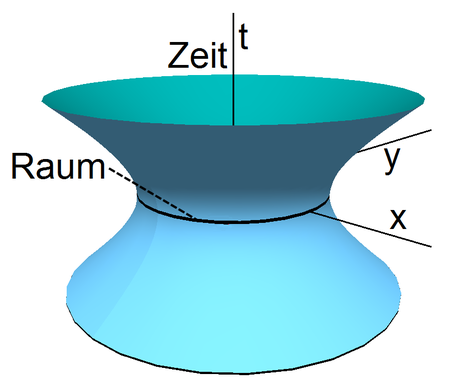
Radius und Volumen erreichen am Zeitpunkt t = 0 ihren Minimalwert (CC BY-SA 4.0)

Der De-Sitter-Raum kann auch definiert werden als Quotient O(1,n) / O(1,1-n) zweier Lorentz-Gruppen, was zeigt, dass er ein symmetrischer Raum ist, aber kein Riemann'scher Raum.

Topologisch ist der De-Sitter-Raum von der Form ℝ × S^n-1.

Die Isometrie­gruppe des De-Sitter-Raumes ist die Lorentz-Gruppe O(1, n). Daher hat die Metrik n(n+1) / 2 unab­hängige Killing-Vektoren und ist maximal symmetrisch. Jeder maximal symmetrische Raum hat konstante Krümmung. Der Riemann'sche Krümmungs­tensor R_ρσμν des De-Sitter-Raumes lautet:

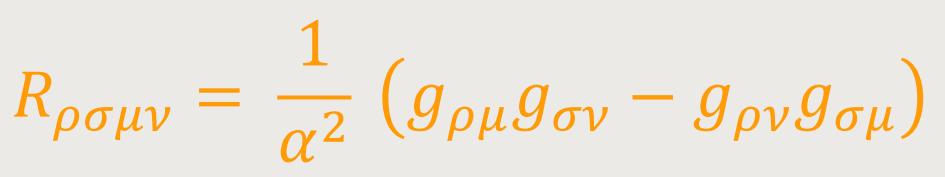
Der De-Sitter-Raum ist eine Einstein-Mannig­faltig­keit, da der Ricci-Tensor R_μν propor­tional zur Metrik g_μν ist:

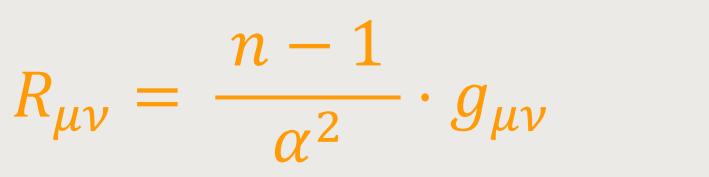
Das heißt, der De-Sitter-Raum ist eine Vakuum­lösung der einsteinschen Feld­gleichungen mit kosmolo­gischer Konstante:

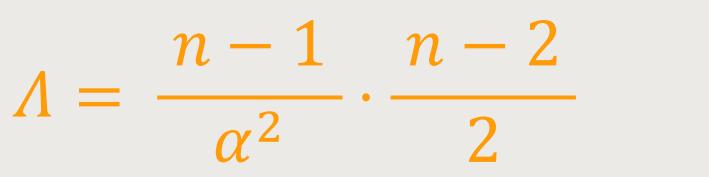
Der Krümmungs­skalar dieses Raumes ist definiert als:

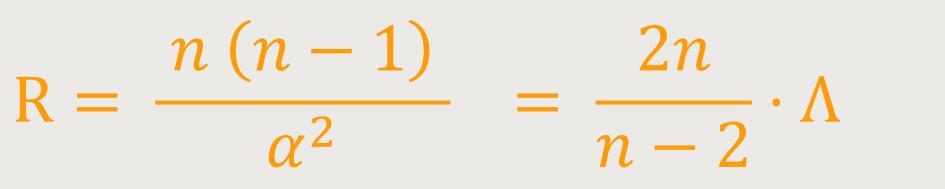
Für n = 4 ergibt sich Λ = 3/α² und R = 4Λ = 12/α².

Für den De-Sitter-Raum lassen sich statische Koordinaten (Zeit t, Radius r ...) wie folgt einführen:

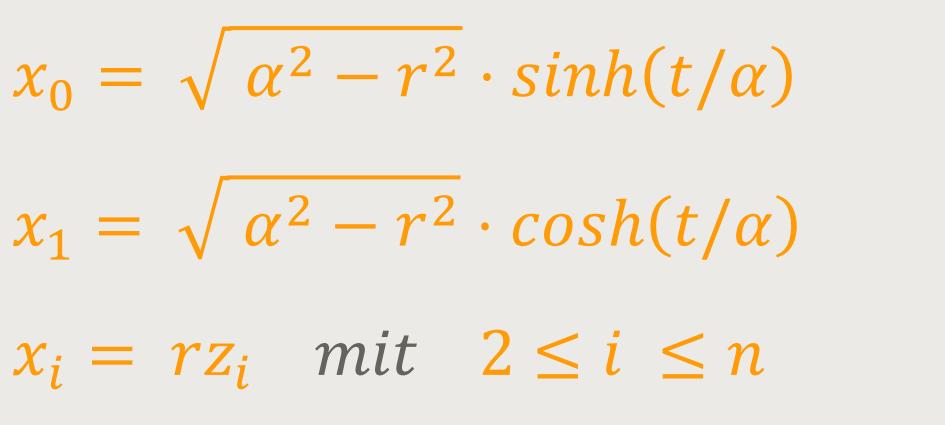
wobei z_i die Standard-Einbettung der Sphäre S^(n-2) in R^(n-1) darstellt.

In diesen Koordinaten nimmt die De-Sitter-Metrik folgende Form an:

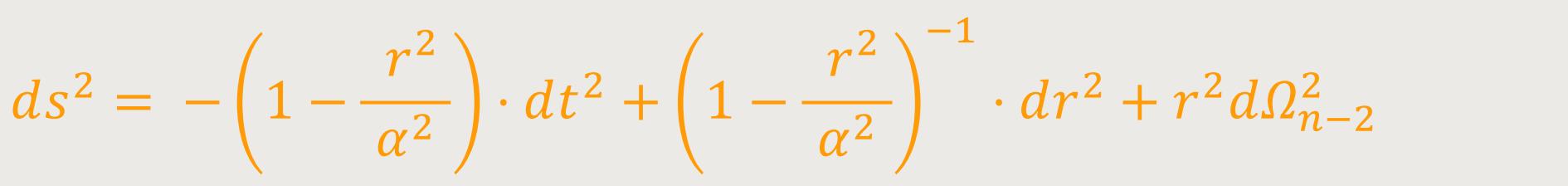
Daraus folgt, es gibt einen kosmolo­gischen Horizont bei r = α.

⇦ Kapitel Kapitel ⇨