Nun folgt eine nähere Beschreibung in Anlehnung an die Originial­schrift von Willem de Sitter, die aus dem Englischen über­setzt wurde. De-Sitter hatte folgende Über­legung:

Wenn man die Gravitations­wirkung jeder gewöhn­lichen Materie, wie zum Beispiel die der Sterne und Planeten vernach­lässigt, und wenn man ein Bezugs­system bestehend aus drei recht­winkligen Raum­koordinaten und der Zeit verwendet, und dieses mit der Licht­geschwindig­keit c multi­pliziert, dann ergibt sich eine 4-dimen­sionale Raum-Zeit, die unseren Beobachtungen entspricht.

Der metrische Tensor g_μν gleicht annähernd der bestehenden Relativitäts­theorie, nämlich (1):

Den Aspekt der Raum-Zeit, der sich gemäß dieser Matrix beschrei­ben lässt, bezeich­nete De-Sitter als „unsere Umgebung”. Im Welt­all erstreckt sie sich mindestens bis zum entfern­testen Stern, Nebel oder Stern­haufen, in welchen wir eindeutige Spektral­linien erkennen können.

Wir wissen nicht, wie sich die g_μν außer­halb unserer Umgebung ver­halten, und jede Annahme über ihre Werte ist nur eine Abschät­zung, deren Unsicher­heit mit der Ent­fernung, entweder im Raum oder in der Zeit, wenn nicht sogar in beiden vom Ursprung aus zunimmt. Wie sich die g_μν in der Unend­lich­keit des Raums und der Zeit verhalten, werden wir nie erfahren.

Aber dennoch besteht eine Not­wendig­keit, Hypothesen zu diesem Thema aufzu­stellen. Eine grobe Abschät­zung zu machen, ist etwas ganz normales und in der klassischen Mechanik üblich, zumal die obigen Werte gemäß (1) für den gesamten Raum und die Zeit bis ins Unend­liche unverän­dert bleiben. Anderer­seits entsteht der Wunsch, Integrations­konstanten oder andere Grenz­werte im Unend­lichen zu verwenden, die in allen Bezugs­systemen gleich sind. Doch obige Werte (1) erfüllen diese Bedingung nicht. Der bevor­zugte und ein­fachste Wert für g_μν im Unend­lichen ist offen­sichtlich Null. Einstein sei es nicht gelungen derartige Werte für die Rand­bedin­gungen fest­zulegen.

Im Nach­folgenden wollte De-Sitter aufzeigen, dass die Hypothese von Einstein äquivalent ist mit einer bestimmten Menge von Werten im Unend­lichen, die der Matrix gemäß (2 A) ent­spricht. Es ist in der Tat offen­sichtlich, dass, wenn die Ausmaße des Universums endlich sind, und eukli­dische Koordi­naten einge­führt werden die g_μν im Unend­lichen notwendiger­weise zu Null werden. Und umgekehrt, wenn die g_μν im Unend­lichen bei einer aus­reichend hohen Rang­ordnung Null, dann ist das Universum endlich in seinen Ausmaßen.

Und daraus würde sich nach De-Sitter die Hypothese ergeben, dass das Universum nicht unend­lich ist, sondern sphärisch. In diesem Fall würden keine Rand­bedingungen benötigt, und das Problem sei aus der Welt.

Aus Sicht der Relativitäts­theorie erscheint es auf den ersten Blick falsch, zu sagen: Die Welt ist sphärisch oder kugel­förmig, obwohl sie sich durch eine Trans­formation analog zu einer stereo­graphi­schen Projektion in einem eukli­dischen Raum dar­stellen lässt. Dies ist eine durch­aus legitime Trans­formation, die die verschie­denen Invarianten ds², G usw. unver­ändert lässt. Aber gerade diese Unveränder­lich­keit zeigt, dass im eukli­dischen Koordinaten­system die Welt in ihren Ausmaßen endlich und sphärisch bleibt. Wenn diese Trans­formation, die Einstein für seine sphärische Welt definiert hatte, auf die g_μν angewendet wird, werden sie in ein Werte­system trans­formiert, dessen Werte schließ­lich verschwinden zu (2A):

Es scheint jedoch, dass die g_μν der Sphären­welt Einsteins, und damit auch ihre trans­formierten Werte im eukli­dischen Bezugs­system, nicht den ursprüng­lich ange­nommenen Differential­gleichungen von Einstein genügen, die wie folgt lauten (3):

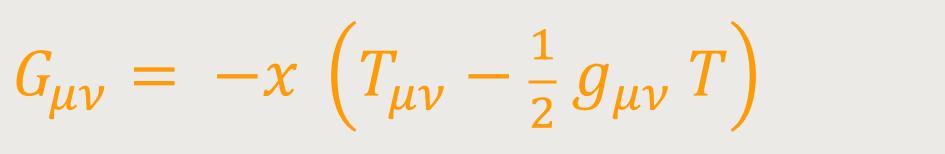
Einstein hielt es daher für notwendig, einen weiteren Term in seiner Gleichung hinzu­zufügen, woraus sich ergibt (4):

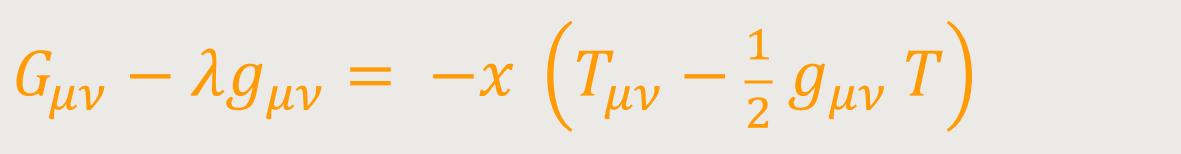
Außerdem wäre es notwendig, den gesamten 3-dimen­sionalen Raum mit Materie anzufüllen, wobei dessen Gesamt­masse so enorm groß ist, dass im Vergleich dazu alle uns bekannte Materie völlig vernach­lässigbar sei. Diese hypothe­tische Materie bezeichnete De-Sitter als „Welt­materie”.

Nach seinen Worten würde Einstein lediglich davon ausgehen, dass der 3-dimen­sionale Raum „endlich” ist. (Zu diesem Zeitpunkt war Einstein tatsächlich von einem statischen Universum überzeugt.)

Aufgrund dieser Annahme bleibt in obigem Werte­system (2A) der Tensor g₄₄ beim Wert Eins, anstatt zu Null zu werden, wie bei den anderen g_μν. Dies war ausschlag­gebend für die Idee, Einsteins Hypothese auf die 4-dimen­sionale Raum-Zeit auszudehnen.

De-Sitter fügte hinzu, dass diese Überlegung, die 4-dimen­sionale Welt sphärisch zu machen, bereits einige Monate zuvor vom damaligen Prof. Ehrenfest im Gespräch mit ihm vorgeschlagen worden sei.

Daraus ergibt sich ein Werte­system der g_μν, in welchem die Werte im Unend­lichen verschwinden zu (2B):

Dadurch ergibt sich nach De-Sitters Worten eine bemerkens­werte Situation, dass nämlich keine „Welt­materie” mehr erforderlich ist.

Um die Ähnlich­keit beider Fälle zu betonen, stellte er beide Syste­me einander gegen­über. Die Gleichung A verweist er auf Einsteins 3-dimen­sionale Hypothese, wogegen sich die Gleichung B auf die hier einge­führte 4-dimen­sionale These bezieht. De-Sitter wollte die Indizes i und j verwenden, wenn sie nur die Werte 1, 2, 3 anneh­men. Die Indizes μ und ν wollte er benutzen, wenn sie die Werte von 1 bis 4 annehmen.

Des Weiteren beschreibt ∑ eine Summe von 1 bis 4 und ∑' die Summe von 1 bis 3 und es gilt σ_μμ = 1, σ_μν = 0 wenn μ ≠ ν.

De-Sitter betrachtete zuerst das von Einstein verwendete Referenz­system. Im Fall A gilt für x₄ = ct, und im Fall B gilt um der Symmetrie willen x₄ = ict. In beiden Fällen ist R der Radius der Hyper­sphäre.

Er fügte hinzu, dass man im Fall B eben­falls x₄ = ct verwenden könnte. Dann wäre die 4-dimen­sionale Welt hyper­bolisch statt sphärisch, aber die Ergebnisse blieben dieselben.

Die g_μν für beide Fälle lauten

... im Fall A:

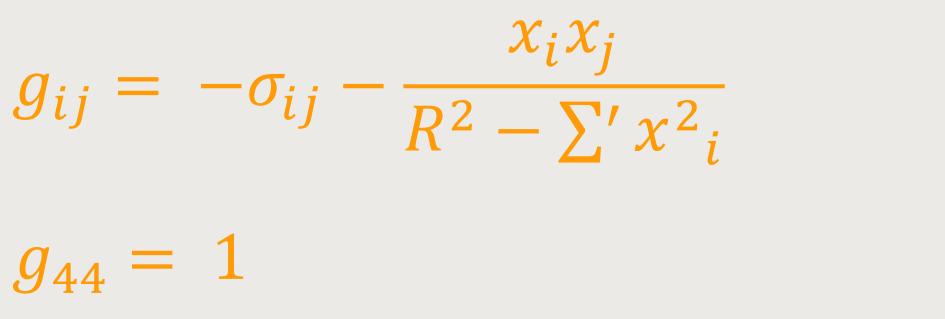
... im Fall B:

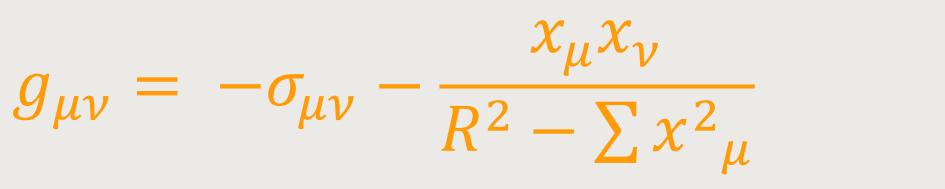
Um den sphä­rischen Charakter besser aufzu­zeigen, führte De-Sitter hyper­sphärische Koordinaten ein, die sich darstellen lassen als

... für Fall A:

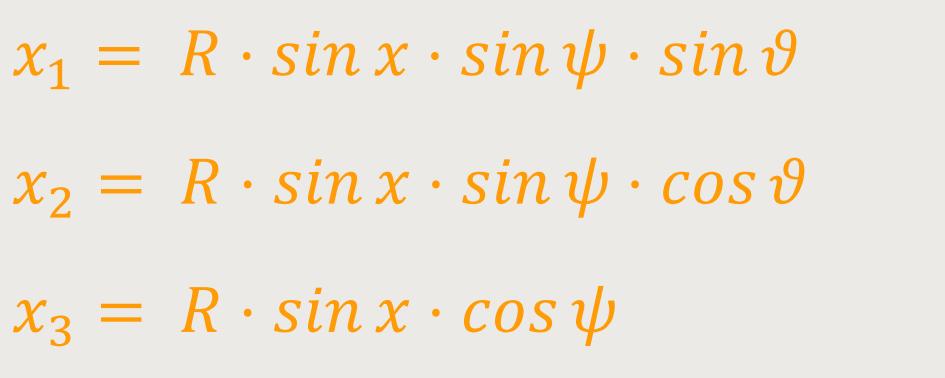
... für Fall B:

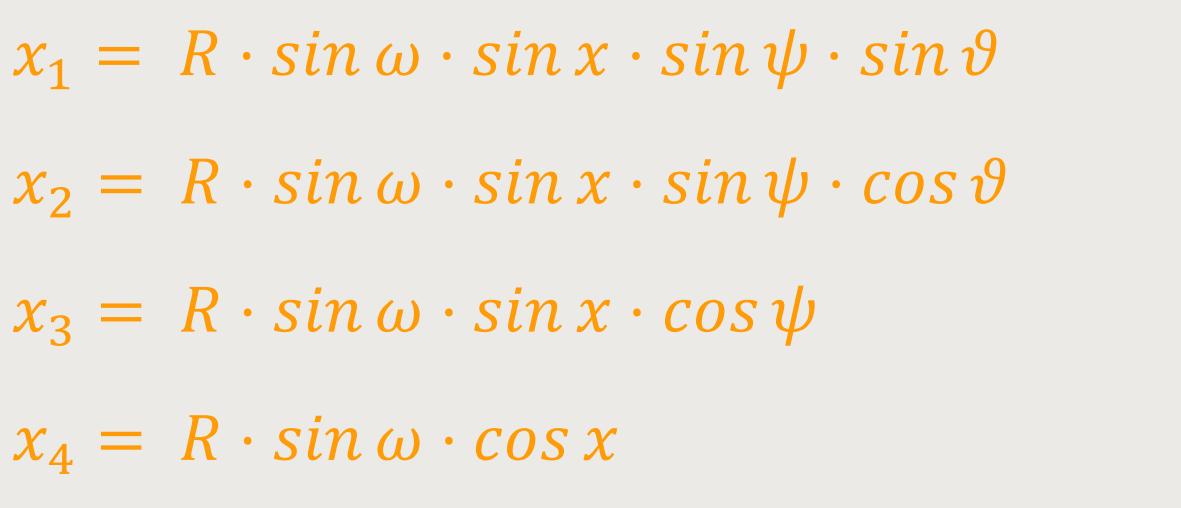
Der Ausdruck für das Integral lautet dann

... im Fall A:

... im Fall B:

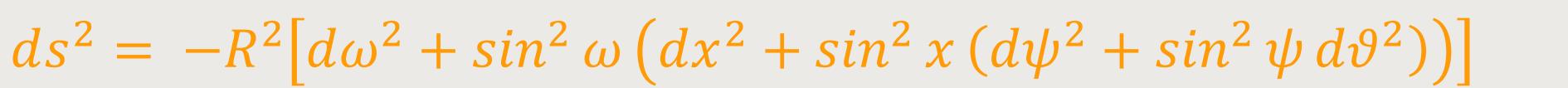
Abschlie­ßend führte De-Sitter die „stereo­grafische Projektion” ein. Sie ist eine Abbildung einer Kugelf­läche in eine Ebene mit Hilfe einer Zentral­projektion. Gleich­zeitig stellte er die karthe­sischen Koordinaten mit folgenden Trans­formationen dar:

Im Fall A:

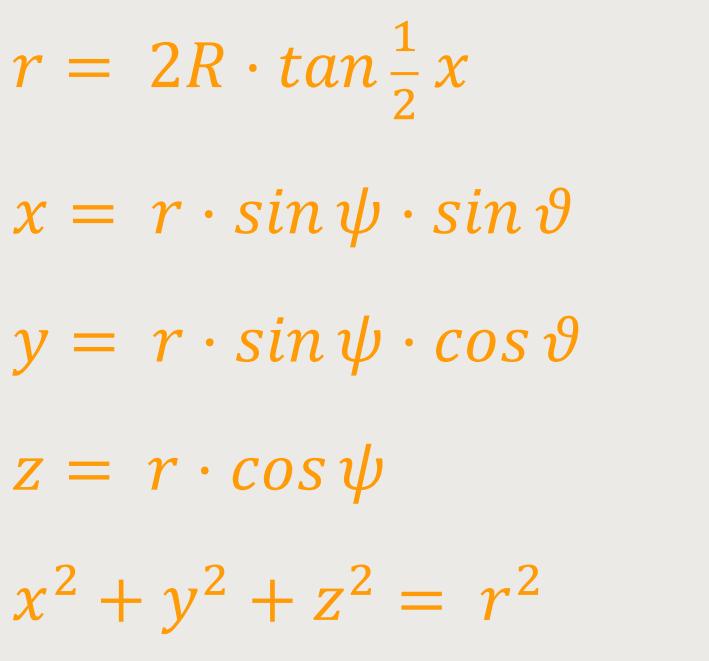
Im Fall B:

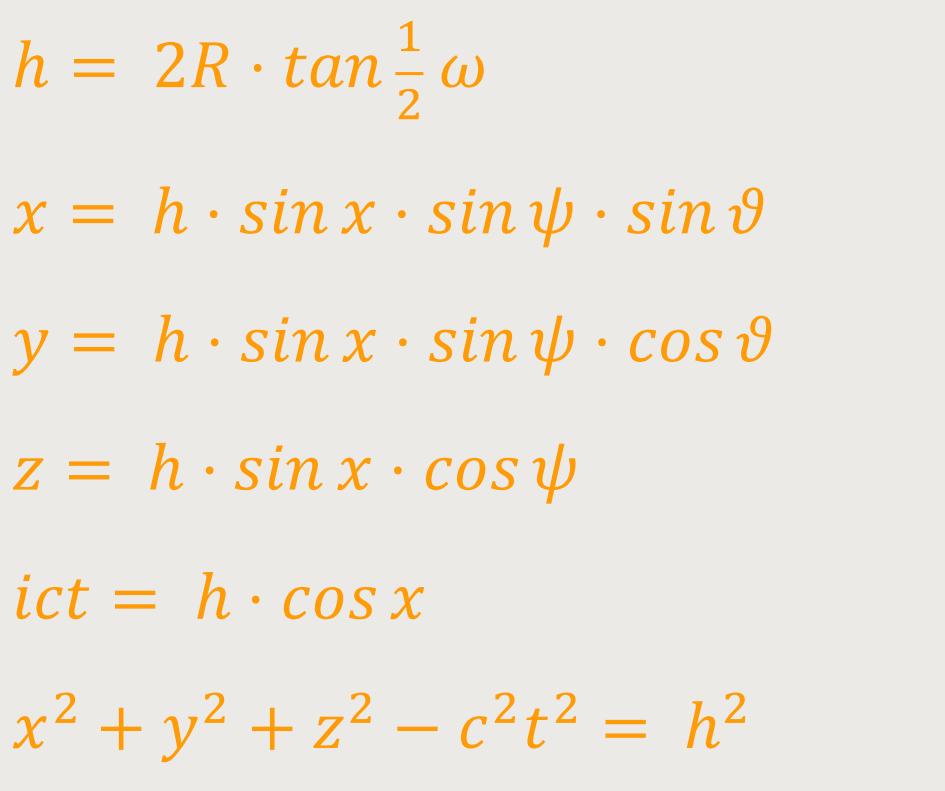
Nach De-Sitters Worten muss eigent­lich nicht darauf hinge­wiesen werden, dass im System A die Variablen x, y, z und im System B die Variablen x, y, z, ict beliebig vertauscht werden können. Des Weiteren gilt:

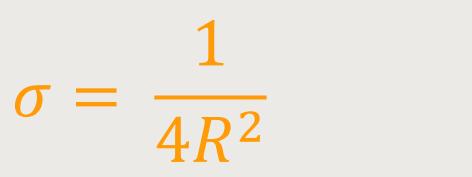
Die g_μν für die Variablen x, y, z, ct werden zu (5)

... im Fall A:

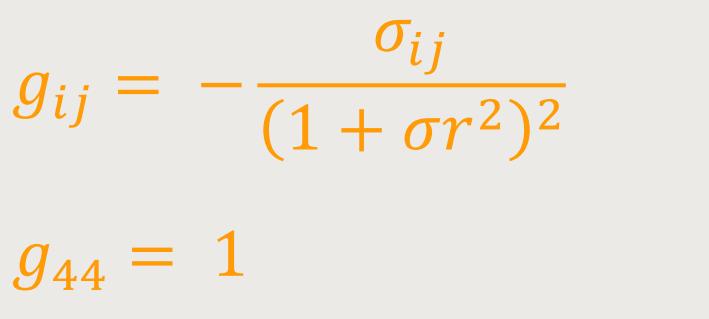
... im Fall B:

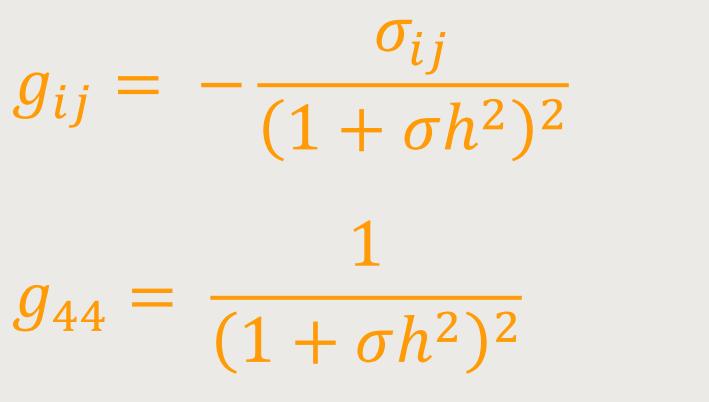
De-Sitter fügte hinzu, dass alle g_μν im System B auf dem „Hyperboloid” unend­lich sind (a):

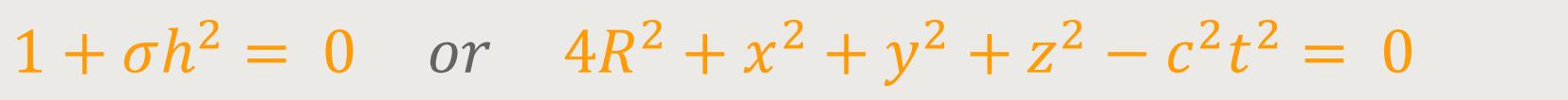
Diese abwei­chende Konti­nuität sei jedoch nur scheinbar. Die 4-dimen­sionale Welt, die wir der Symmetrie willen als kugel­förmig darge­stellt haben, ist in Wirklich­keit hyperbo­lisch und besteht aus Schalen, die erst im Unend­lichen mit­einander verbunden sind. Die Gleichungen beinhalten beide Schalen, aber nur eine von ihnen repräsen­tiert das gegen­wärtige Universum. Das Hyper­boloid nach vorheriger Gleichung gemäß (a) bildet eine Grenze zwischen beiden Teilen des eukli­dischen Raums x, y, z, ct, die diesen beiden Schalen ent­sprechen. Der Raum wird von der Zeitachse t an den Punkten ct = ± 2R geschnitten, dessen Abstand vom Ursprung die Ausmaße hat:

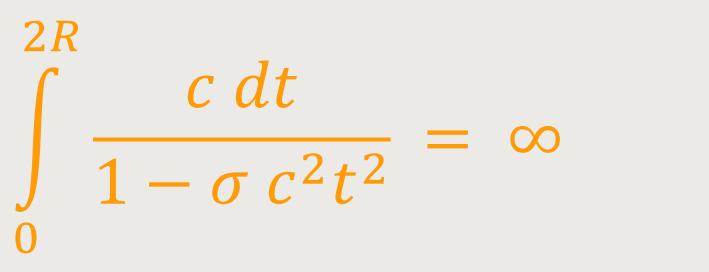
Die Länge der Halb­achse von x hat in beiden Systemen die Ausmaße:

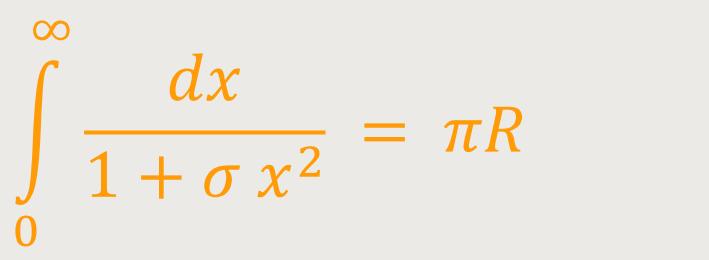
Alle g_μν außer­halb der Diagonalen haben den Wert Null. Wenn σ sehr klein ist, haben die g_μν für mittlere Werte von r und h unge­fähr die Werte wie gemäß der Matrix (1). Im Unend­lichen hängen sie von den Werten gemäß (2A) und (2B) ab, die bereits oben angegeben wurden.

Um die Beziehung zwischen σ und λ zu finden, muss man die Werte aus obigen Gleichungen (5) in die Gleichungen (4) einsetzen. Nach De-Sitters Erkenntnis lassen sich die Werte auch in jedes andere Bezugs­system über­tragen.

Es muss dabei die Möglich­keit in Betracht gezogen werden, dass es notwendig sein könnte, eine „Welt­materie” einzu­führen. Wir ver­nach­lässigen zunächst die gesamte vorhandene Materie und nehmen an, dass die Welt­materie gleich­mäßig und ruhend im gesamten Raum verteilt ist, sodass T₄₄ = g₄₄ · ϱ, und alle anderen T_μν = 0 sind.

Gemeint ist eine Verteilung, in der ϱ konstant ist, wobei mit ϱ die Dichte in den Abmessungen gemeint ist. Im Koordinaten­bereich ist die Dichte natürlich nicht konstant, aber im System x, y, z, ct geht sie im Unend­lichen gegen Null.

Die Feldgleichungen werden dann zu

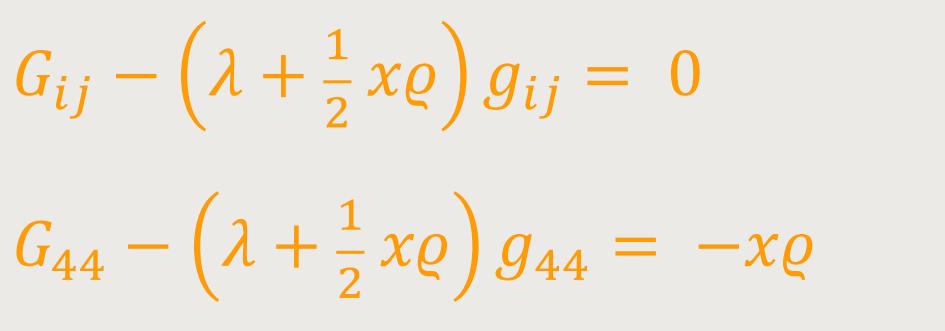
Für die Größen G_μν ergeben sich die zwei Systeme:

System A:

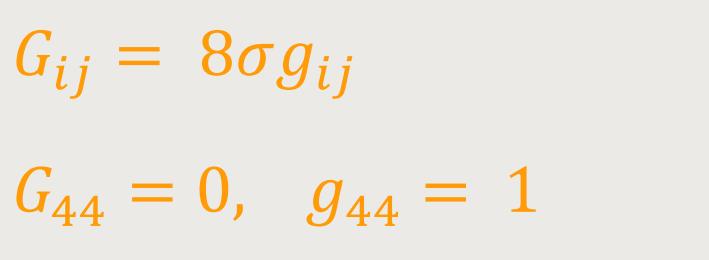
System B:

Für die dann gilt (6)

... im Fall A:

... im Fall B:

Das Ergebnis für A ist das Gleiche wie von Einstein entdeckt wurde. Für das System B gilt ϱ = 0, was nach De-Sitters Feststellung bedeutet, dass die hypothe­tische Welt­materie nicht existiert.

Welches der drei Systeme soll nun bevorzugt werden? Das System A mit der „Welt­materie”, oder das System B ohne diese? Viel­leicht aber beide Systeme, mit den Feld­gleichungen gemäß (4) und einem metrischen Tensor g_μν, der im Unend­lichen der Matrix (2A) oder (2B) entspricht? Oder vielmehr das ursprüng­liche System ohne Welt­materie, mit den Feld­gleichungen (3) und dem Tensor g_μν aus (1), deren Werte im Unend­lichen gleich bleiben?

Um aus rein physika­lischer Sicht die Phäno­mene in unserer Umge­bung zu beschreiben, sind diese Fragen belanglos. In unserer Umgebung entspre­chen die g_μν in allen Fällen inner­halb der Genauigkeits­grenzen unseren Beobachtungen gemäß der Matrix (1), und die Feld­gleichung gemäß (4) unter­scheidet sich nicht von (3). Die Frage ist also eigent­lich: Wie kann man das, was außer­halb unserer Umgebung liegt, abschätzen? Die Wahl kann daher nicht durch physika­lische Argumente getroffen werden, sondern muss von meta­physischen oder philo­sophischen Erwägungen abhängen, wobei natür­lich persön­liche Ansichten oder Vorlieben einen gewissen Einfluss haben werden.

Nun zu der eigent­lichen Frage: Wenn die gesamte Materie nicht existieren soll, mit Ausnahme des materiellen Punktes, der als Prüf­körper verwendet werden soll, besitzt dieser Prüf­körper dann eine Träg­heit oder nicht? Nach der Lehr­meinung von E. Mach lautete die Antwort seiner­zeit NEIN. Aber gemäß unserer Erfahrung lautet die Antwort ganz entschieden JA, wenn mit der gesamten Materie die gewöhn­liche physika­lische Materie gemeint ist, wie z. B. Sterne, Nebel oder Stern­haufen. Die Befürworter von E. Mach sind also gezwungen von vorhandener Materie auszugehen, nämlich der Welt­materie. Wenn wir uns auf diesen Stand­punkt begeben, müssen wir notwendiger­weise das System A bevorzugen, welches als einziges eine Welt­materie zulässt.

De-Sitter fügte hinzu, dass die Hypothese, die vormals von Einstein vertreten und von De-Sitter bestritten wurde, mit den Gleichungen gemäß (3), bei sehr großen Massen, bezogen auf sehr große Entfernungen, möglich wäre. Dadurch würde man für g_μν Werte erhalten, die sich im Unendlichen zu einer invarianten Matrix auflösen würden, wie selbst Einstein es für möglich gehalten hat.

Diese Welt­materie diente nach De-Sitters Worten jedoch keinem anderen Zweck, als es möglichst nach­zuvoll­ziehen, dass sie nicht existiert. Nun zeigt die Gleichung gemäß (6), dass, wenn sie nicht existiert, gilt ϱ = 0, und die Feld­gleichungen sind nicht erfüllt. Angenommen, die Welt­materie existiert nicht, obwohl dies aus logischer Sicht unmöglich ist, dann ent­spricht im System A die Welt­materie dem 3-dimen­sionalen Raum oder ist zumindest untrennbar mit ihm verbunden.

De-Sitter ging so weit zu sagen, dass man auch das Postulat von E. Mach aufgeben und durch das Postulat ersetzen könnte, dass im Unend­lichen die g_μν oder nur die g_ij im 3-dimen­sionalen Raum zu Null werden, oder zumindest unverän­dert bleiben für alle Trans­forma­tionen. Dieses Postulat würde auch beinhalten, dass es möglich sein muss, im gesamten Universum beliebige Bewegungen auszu­führen, die niemals durch eine Beobachtung fest­gestellt werden können. Die 3-dimen­sionale Welt muss, um „Bewegungen” aus­führen zu können, das heißt dass seine Lage eine veränder­liche Funktion der Zeit ist, sich in einem absoluten Raum von drei oder mehr Dimensionen (nicht der Raumzeit x, y, z, ct) befinden. Die 4-dimen­sionale Welt erfordert für ihre „Bewegung” einen vier- oder mehr­dimen­sionalen absoluten Raum und darüber hinaus eine außer­welt­liche „Zeit”, die für diese Bewegung als unabhängige Variable dient. All dies zeigt, dass das Postulat der Invarianz der g_μν im Unend­lichen keine physika­lische Bedeutung hat. Es sei reine Mathe­matik!

Das System A, welches im End­effekt die Werte gemäß der Matrix (2A) für die g_μν beinhaltet, erfüllt dieses Postulat, wenn es nur auf die 3-dimen­sionale Welt ange­wendet wird, und wenn man nicht für alle Trans­forma­tionen Invarianz verlangt, sondern nur für die­jenigen, die im Unend­lichen t' = t entsprechen.

Also ist eine gewöhn­liche Lorentz-Trans­formation wie

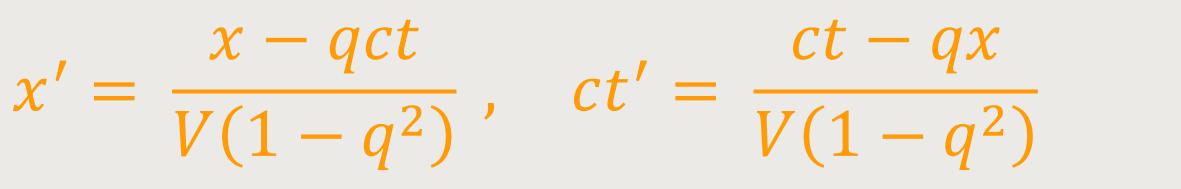
... im System A nicht erlaubt, und muss ersetzt werden durch:

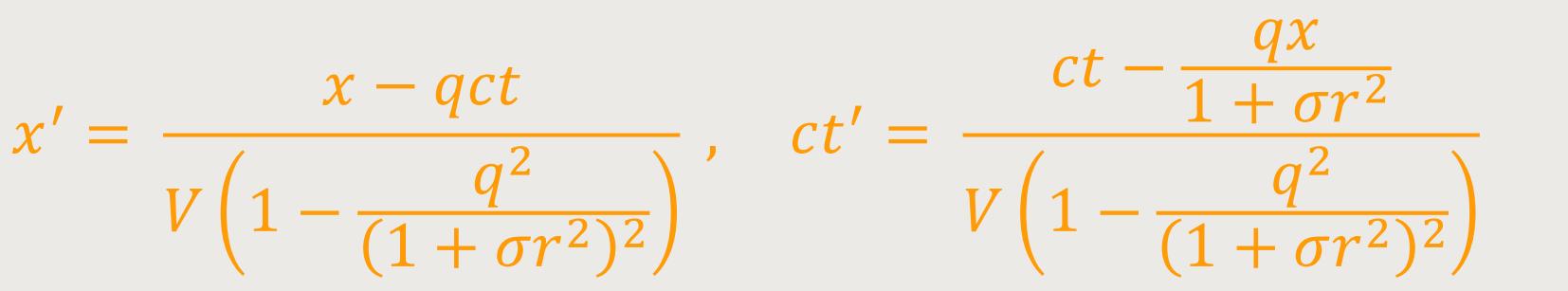
Wird das Postulat auf die 4-dimen­sionale Welt und auf alle Trans­forma­tionen ange­wendet, dann ist das System B das einzige, welches dies erfüllt. Wir stellen also fest, dass die Zeit im System A eine abge­sonderte Stellung hat. Dass dies so sein muss, ist a priori klar. Denn wenn von der 3-dimen­sionalen Welt die Rede ist, was nicht gleich­bedeutend ist mit der Einfüh­rung einer absoluten Zeit, impliziert zumindest die Hypothese, dass es an jedem Punkt des 4-dimen­sionalen Raums eine definierte Koordinate x₄ gibt.

Diese ist allen anderen Koordinaten als „Zeit” vorzu­ziehen, und an allen Stellen wird nur diese Koordinate als Zeit gewählt. Dieser funda­mentale Unter­schied zwischen der Zeit und den Raum-Koordi­naten, scheint im Wider­spruch zu der völligen Symmetrie der Feld­gleichungen und der Bewegungs­gleichungen (Gleichungen der geodä­tischen Linie) bezüg­lich der vier Variablen zu stehen.

Auf einige Merkmale der Systeme A und B wies De-Sitter noch hin. Im System A sei die Licht­geschwin­dig­keit variabel, und zwar im System x, y, z, ct. Im Unend­lichen wäre sie theoretisch sogar unend­lich. Im System x, ψ, ϑ, ct bliebe sie dagegen konstant.

Im System B herrschen immer und überall gleiche Bedingungen. Aus den Tatsachen, dass man Spektral­linien der entfern­testen uns bekannten Objekte wie den Spiral­nebeln identi­fizieren kann und dass die Parallaxen dieser Objekte nicht negativ sind, kann man schließen, dass bei diesen Entfer­nungen die Werte immer noch bei ungefähr g_ij = −σ_ij, g₄₄ = 1 liegen und folg­lich muss im System A das σr², und im System B das σh² sehr klein sein. Im Fall A kann man auf diese Weise eine Ober­grenze für σ ableiten. Anderer­seits erhält man im System B als Folge der Konstanz der Licht­geschwin­dig­keit h² = 0 für alle rein optische Beobachtungen, vorausgesetzt man vernach­lässigt den Einfluss der Materie.

Was die Wirkung von σ auf die Planeten­bewegungen betrifft: In beiden Fällen ist die Orbital­ebene nicht gestört. Im Fall A gibt es hier keine säkularen Terme, die abhängig sind von σ.

Im Fall B sind die ent­haltenen Terme aufgrund von σ unter­geordnet, aufgrund der Tatsache, dass alle g_μν explizit von der Zeit abhängen. Die Bewegung im Perihel lautet dann:

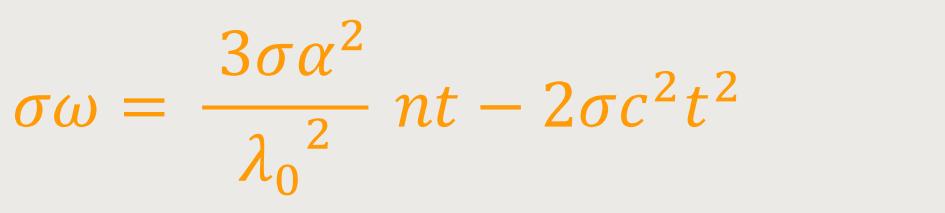
... und auch die anderen Elemente haben Terme mit c² t² so lautet zum Beispiel der Parameter der Ellipsen­bahn:

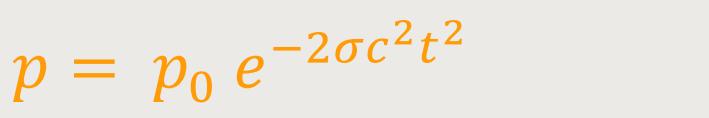
... wobei λ₀² = (x · m) / 8π; m ist die Masse der Sonne, und e = 2,718 (die Eulerzahl). Nach unserer Erfahrung sind diese „Störungen” unmerklich, sodass man auch hier eine Obergrenze für σ festlegen kann.

Die unter­geord­neten Terme bei den „Störkräften” lauten in beiden Fällen wie folgt:

Im Fall A:

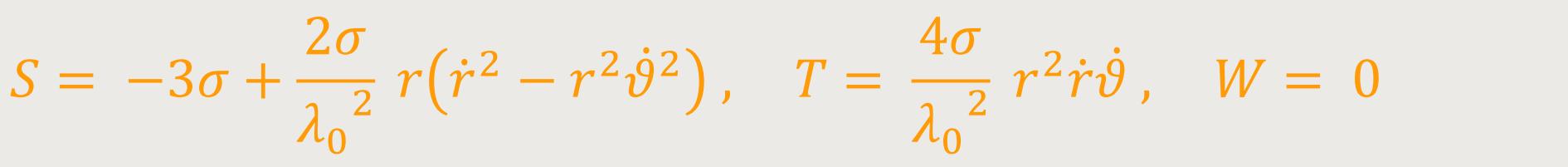
Im Fall B:

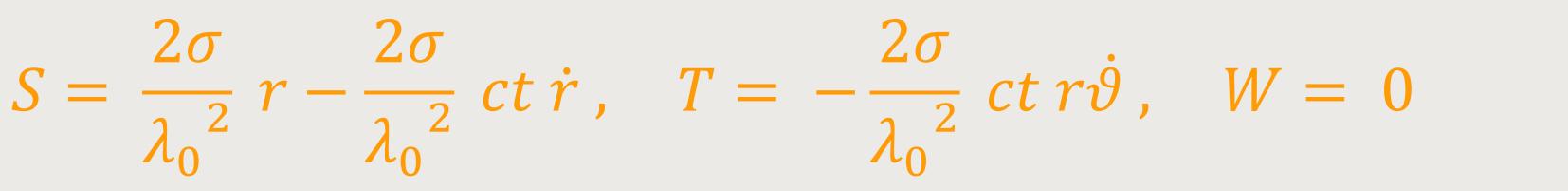
Hierzu ergänzt De-Sitter noch: Die Bezeich­nungen mit c² t² im Fall B entstehen dadurch, dass sowohl die Einheiten für die Zeit als auch den Raum (im Koordinatenmaß) abhängig sei von der Zeit.

De-Sitter war nicht daran gelegen, diese Ober­grenze genau zu bestimmen. Für beide Fälle könnte man annehmen, dass σ < 10^-24 zum Beispiel in Astrono­mischen Einheiten (AE), oder 2σ < 10^-50 in Zentimetern ist. Er fügte hinzu, dass die Dichte der Welt­materie im System A dann ϱ < 3,10^-17 (AE) beträgt oder ϱ < 2,10^-23 (CGS-Einheiten). Dies entspricht der Masse eines Sterns (vergleichbar mit unserer Sonne) mit einer Sphäre bzw. einem Radius von 1 Parsec.

Man könnte aller­dings eine „Ober­grenze” für σ fest­legen. Um den Wert dieser Konstante zu bestimmen, wäre es notwendig, dass sie einen mess­baren Einfluss auf irgendein physika­lisches oder astrono­misches Phänomen hat. De-Sitter war davon überzeugt, dass es natürlich nicht von vorn­herein auszu­schließen ist, dass irgend­wann in der Zukunft Beobachtungen vorge­nommen werden, oder Phänomene entdeckt werden, die mit Hilfe der Konstante σ erklärt werden können.

Aber zu De-Sitters Zeiten waren keine solchen Phänomene bekannt, und es gab auch keine Hinweise auf irgend­etwas in dieser Richtung. Die Konstante σ diente nach seinen Worten ledig­lich dazu, eines von vielen welt­anschau­lichen Bedürf­nissen zu befriedigen, aber es sei nicht wirklich von physika­lischer Bedeutung, obwohl es mathe­matisch als Raum-Krümmung inter­pretiert werden kann.

Letztlich könnte man auch beide Systeme A und B vernach­lässigen und bei den ursprüng­lichen Feldg­leichungen (3) und den Werten (1) für g_μν bleiben, die sich im Unend­lichen nicht verändern. Damit sei die Träg­heit zwar nicht erklärt. Doch man sollte sie lieber ungeklärt lassen, als sie mit einer unbestimmten bzw. unbestimm­baren Konstante λ zu erklären. De-Sitter räumte ein, dass die Einführung dieser Konstante von der Symmetrie und Eleganz von Einsteins ursprüng­licher Theorie abweicht. Insofern bliebe Einsteins Theorie unschlagbar, weil sie so vieles erklärt, ohne eine neue Hypothese oder eine empirisch gewählte Konstante einzu­führen.

Willem de Sitter hatte in einem regen Brief­wechsel mit Einstein die wesent­lichen Inhalte obiger Abhandlung mit­geteilt. In einem seiner Antwort­schreiben äußerte sich Albert Einstein mit den Worten:
„Es wäre nach meiner Meinung unbefriedigend, wenn es eine denkbare Welt ohne Materie gäbe. Das g_μν-Feld soll vielmehr durch die Materie bedingt sein, [d. h.] ohne dieselbe nicht bestehen können. Das ist der Kern dessen, was ich unter der Forderung von der Relativität der Träg­heit verstehe.” (24.03.1917)

Aus De-Sitters Sicht hätte Einstein das postuliert, was De-Sitter selbst in obiger Abhandlung die logische Unmöglich­keit genannt hat, dass Materie nicht existiert. Man könnte es nach seinen Worten das „Materie-Postulat” von der Relativität der Träg­heit nennen. Dieses kann nur erfüllt werden, wenn man das System A mit „seiner” Welt­materie wählt, d. h. die Konstante λ einführt und der Zeit eine eigene Stellung unter den vier Koordinaten zuweist.

Anderer­seits gibt es das „mathe­matische Postulat” der Relativi­tät der Träg­heit, d. h. das Postulat, dass die g_μν im Unend­lichen invariant (unverändert) lässt. Gemäß diesem Postulat, welches wie bereits erwähnt keine wirkliche physika­lische Bedeutung hat, macht Materie keinen Sinn. Es kann dennoch erfüllt werden, indem man das System B ohne eine Welt­materie wählt und mit unein­geschränkter Relativi­tät der Zeit.

Aber auch hier benötigt man die Konstante λ. Die Einfüh­rung dieser Konstante kann nur vermieden werden, wenn man das Postulat von der Relativität der Träg­heit voll­ständig aufgibt.

Quellen

W. de Sitter, On the relativity of inertia. Remarks concerning Einstein's latest hypothesis, in: KNAW, Proceedings, 19 II, 1917, Amsterdam, 1917, pp. 1217-1225.

Vorliegende Übersetzung, Volker Rödel ©, Hessen 2018.

⇦ Kapitel Kapitel ⇨