Bisher haben wir uns nur mit dem Wellenaspekt des Lichts beschäftigt. Nun werden wir den Fokus noch kurz auf den Teilchenaspekt des Lichts betrachten.
In der Realität kann man sehr viel mit klassischen Methoden beschreiben. Aber vieles darüber hinaus lässt sich nur mit quantenmechanischen Methoden ergründen. So war es Max Planck, der als erster versuchte, die Wärmestrahlung mittels Quantenhypothese zu beschreiben. Und einige Jahre später hatte Albert Einstein die Idee, dass das Licht nicht nur einer elektromagnetischen Welle gleicht, sondern auch Teilcheneigenschaften hat.
Ein sehr wichtiges Experiment im Jahre 1909, das sogenannte „Ehrenhaft-Millikan-Experiment”, beschreibt, dass die elektrische Elementarladung nur in Quanten vorkommt. Es wurde gezeigt, dass es ein elektrisches Elementarquantum gibt und dass keine Teilchen existieren, deren Ladungen kleiner sind als ein solches Elementarquantum. Andererseits stellt sich jede Ladung nur als ein Vielfaches dieses Elementarquantums dar. Elektronen und Protonen tragen als Ladung ein solches Elementarquantum.
Doch bereits 1887 hatte Heinrich Hertz die ersten Experimente zum sogenannten Photoeffekt gemacht. Da sich die Elektronen bei den Metallen in den obersten Energielevels relativ frei bewegen können, verursachen diese den Stromfluss in den Metallen. Man spricht in diesem Zusammenhang auch von den Leitungselektronen. Andererseits gibt es eine gewisse Austrittsarbeit, aufgrund der solche Elektronen das Metall verlassen. Wird diese Arbeit nicht aufgewendet, bleiben die Elektronen in dem Metall.
Die Spannungsreihe hat aufgezeigt, dass es Metalle gibt, bei denen diese Austrittsarbeit relativ hoch ist, bei anderen dagegen niedriger. Somit ist es bei den edleren Metallen schwieriger, Elektronen aus dem Verband herauszulösen. Zink ist zum Beispiel ein Metall, bei dem nur geringe Austrittsarbeit von Nöten ist. Dennoch ist es so, wenn man eine Zinkplatte elektrisch auflädt, dass die Austrittsarbeit ansteigt, um Elektronen aus der Oberfläche herauszulösen.
Und so hatte Hertz im Jahr 1887 die Idee, eine Zinkplatte mit Licht zu bestrahlen. Je intensiver dieses Licht wird, desto mehr Energie wird auf das Zink übertragen, sodass letztlich Elektronen die Zinkoberfläche verlassen. Dieser Vorgang wird auch als Photoelektrischer Effekt bezeichnet.
Grafik (wird später eingefügt)
Das bedeutet im Detail, dass das Licht in Quanten auf eine solche Zinkplatte auftrifft. Die Energie jedes dieser Lichtquanten steht aber nicht mit der Lichtintensität in Zusammenhang, sondern vielmehr mit der Frequenz des Lichts.
Und es war Albert Einstein, der 1905 herausfand, dass nicht die Lichtintensität, sondern die höher frequentierte ultraviolette Strahlung für diesen Effekt verantwortlich ist. Er war es, der die Lichtquantenhypothese aufgestellt hat:
Licht kann aufgefasst werden in Form von Teilchen (Photonen) mit einer Energie h · ν.
h ist eine Proportionalitätskonstante
ν ist die Frequenz des Lichts
Die Energie eines solchen Photons ist proportional zur Frequenz.
Das Plancksche Wirkungsquantum wird auch definiert als:

Somit ist die Arbeitsenergie der Elektronen, die aus der Oberfläche heraus geschlagen werden, definiert als:
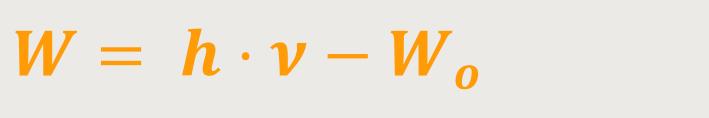
Wo ist die Austrittsarbeit
In diesem Zusammenhang hat Hertz auch nachgewiesen, dass das Licht als elektromagnetische Wellen aufgefasst werden kann.
Die bisherige Betrachtung hat also gezeigt, dass es hier einen Dualismus gibt. Licht kann als Welle und als Teilchen aufgefasst werden.
Entsprechend des Teilchenaspektes des Lichts, ist die Energie eines Lichtteilchens (Photon) definiert als:

ω = 2π · ν ist die Austrittsarbeit
Meistens schreibt man in der Beziehung ω statt ν, als reduziertes Wirkungsquantum.
Wenn die Photonen aber tatsächlich Teilchen sind, kann man davon ausgehen, dass diese Teilchen einen Impuls aufweisen. Nun gilt es, diesen Impuls auszurechnen.
Das bedeutet wiederum, dass sich die Photonen mit Lichtgeschwindigkeit ausbreiten. Natürlich ist es so, dass bei herannahen an die Lichtgeschwindigkeit die dynamische Masse eines Teilchens über alle Grenzen anwächst. Daher muss die Ruhemasse gleich Null sein, auch wenn die Photonen im klassischen Sinn nicht ruhen. Insofern haben die Photonen eine entsprechende Energie und eine entsprechende Masse.
Wir hatten bereits die Beziehung erarbeitet:
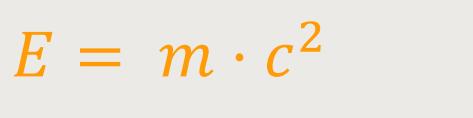
Anderseits kennen wir auch den Ausdruck für den Impuls:

Wenn wir beide Gleichungen miteinander in Beziehung setzen, ergibt sich:
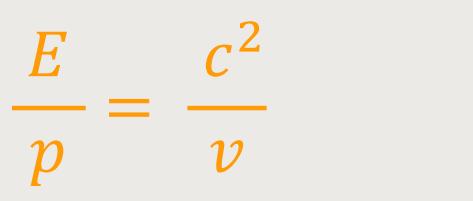
Da wir es aber mit Photonen zu tun haben, entspricht
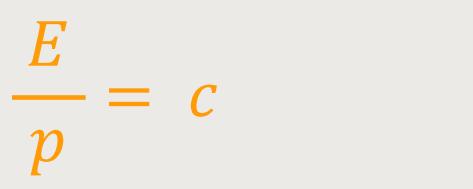
Und damit erhalten wir zunächst für den Impuls eines Photons:
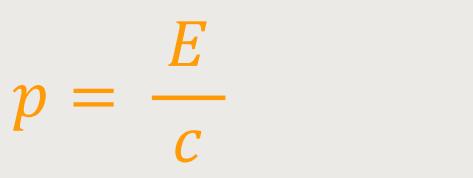
Oder anders ausgedrückt:
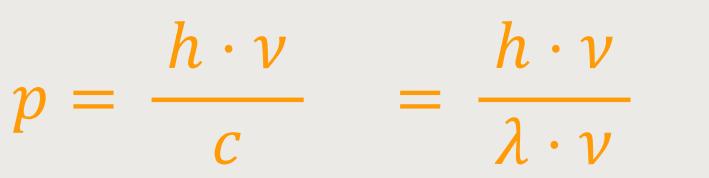
λ · ν ist die Phasengeschwindigkeit
Die Wellenlänge war ja definiert als:
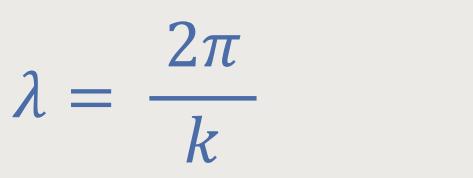
k ist die Wellenzahl
Durch Einsetzten erhält man entsprechend:
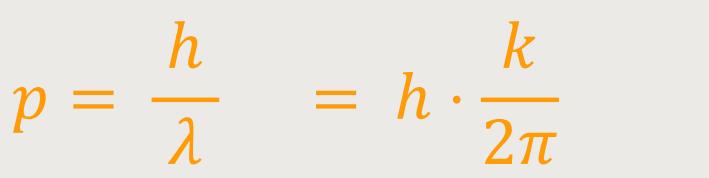
Und damit erhalten wir tatsächlich für den Impuls eines Photons:

Damit wird das Licht aufgefasst als Teilchen mit einer Energie E und einem Impuls p. Wird das wiederum mit dem Wellenaspekt des Lichts in Verbindung gebracht, ergibt sich ein Welle-Teilchen-Dualismus.
Grafik / Folie (wird später eingefügt)
1927 haben Davisson & Germer die berühmten Interferenzversuche mit Elektronenstrahlen gemacht.
...
Grafik / Folie (wird später eingefügt)
Selbst bei Elektronen erhält man ein entsprechendes Beugungsmuster. Und damit zeigt sich, dass auch aus anderer Sicht Teilchen Welleneigenschaften besitzen.
Und so ergibt sich jetzt aufgrund obiger Überlegungen, dass man zu den Teilchen die „De-Broglie-Wellen” einführt. Meistens bezeichnet man sie auch als Materiewellen. Denn wenn man den Impuls des Teilchens kennt, erhält man sofort die De-Broglie-Wellenlänge:
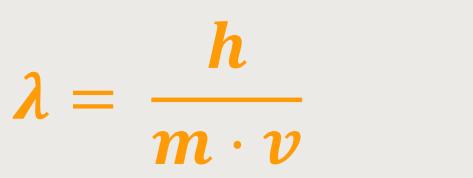
m entspricht hier der Elektronenmasse (1/1836 der Protonenmasse)
Damit ergibt sich, dass man für makroskopische Teilchen extrem kleine Wellenlängen erhält.
Beispielrechnung:

Das heißt, für „makroskopische” Teilchen ist der Wellenaspekt praktisch unsichtbar.
De Broglie hat diesen Wellenaspekt benutzt, um zu zeigen, dass man damit die Quantenhaftigkeit der Energieniveaus bei den Elektronen in der Elektronenhülle eines Atoms feststellen kann.
Es ging darum zu erklären, wieso es zu der Quantisierung der Energie der Hüllenelektronen in den Atomen kommt. Dass es eine Quantisierung gibt, war schon seit längerem bekannt. Es gibt nämlich Spektren bei verschiedenen Materien, die sich beim Verbrennen in einer Flamme in einer ganz genau definierten Farbe darstellt, was dann einer ganz bestimmten Frequenz entspricht.
Es sind also Photonen, mit einer genau definierten Frequenz. In dem Atom muss daher etwas Bestimmtes passieren, damit eine genau definierte Energie frei wird. Daher müssen die Atomhüllen quantisierte Energien haben.
Grafik (wird später eingefügt)
Wenn sich eine bestimmte Anzahl von Wellenlängen ergibt, erhält das Atom einen in sich geschlossenen Zustand. Deshalb sind auch nur bestimmte Frequenzen und Wellenlängen möglich. Und mit bestimmten Frequenzen ergeben sich auch nur bestimmte diskrete Elektronenenergien in der Atomhülle.
Um das zu untermauern, gab es 1914 den Franck Hertz-Versuch. Hierfür wurde eine längliche Elektronenröhre verwendet. Auf der einen Seite befindet sich eine Glühkathode und auf der anderen Seite eine Anode. Die angelegte Spannung kann entsprechend von außen gemessen werden. In der Röhre befindet sich im wesentlichen Vakuum und ein kleines Gefäß mit Quecksilber, sodass sich Quecksilberdampf mit geringer Konzentration in der Röhre ausbreiten kann.
Wenn die Elektronen von der Kathode zur Anode wandern, werden die Elektronen auf ihrem Weg mit einzelnen Quecksilberatomen zusammenstoßen. Solang die Elektronen keine ausreichend hohe Energie haben, um eine diskrete Energiedifferenz in der Elektronenhülle des Quecksilberatoms zu überschreiten, können sie ihre Energie nicht abgeben. Deshalb werden die Elektronen nur elastisch zusammenstoßen und weiterfliegen.
Dennoch wird ihre kinetische Energie laufend größer, bis sie schließlich doch noch einen Energieübergang in der Elektronenhülle bewirken. In diesem Fall kommt es zu einem nichtelastischen Stoß und die Elektronen verlieren ihre ganze Energie, bleiben stehen, und ihre Energie springt auf die Quecksilberatome über. Die angeregten Hüllenelektronen fallen anschließend wieder zurück und senden dabei ein Photon aus.
Ausgehend von einer kleinen Spannung, erhöht sich der Strom immer mehr, sobald auch die Spannung erhöht wird. Sobald eine bestimmte Spannung erreicht ist, bei der die Elektronen, noch bevor sie die Anode erreichen, bereits unelastisch mit einem Quecksilberatom zusammenstoßen konnten, verharren die Elektronen an Ort und Stelle und der Strom geht zurück. Auf diese Weise lässt sich bei stetig zunehmender Spannung ein Auf und Ab des Stromes beobachten.
Mit einem digitalen Transientenrekorder lassen sich diese Stromschwankungen sehr schön bei stetig zunehmender Spannung visualisieren. Die Schwingungen der Stromkurve, die sich daraus ergeben, lassen sich mit der Wellengleichung beschreiben.
Erwin Schrödinger hat 1926 eine nicht relativistische Wellengleichung für massive Teilchen aufgestellt. Denn die Photonen haben Ruhemasse Null. Aber die Elektronen haben dagegen eine Masse.
Und diese berühmte „Schrödinger-Gleichung” lautet:
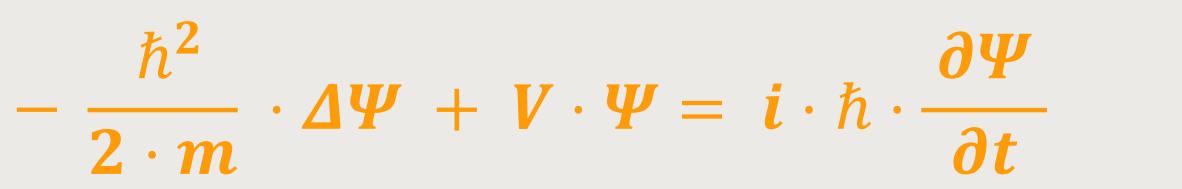
Ψ ist die wellenhafte Auslenkung
V ist das entsprechende Potenzial
Das ist im Wesentlichen die Wellengleichung für die Materiewellen.
Es geht um ein Teilchen, das eine bestimmt Masse m hat und sich in einem Potential V befindet. Mit dieser Gleichung lässt sich die Wellenfunktion in der Umgebung von Atomkernen ausrechnen.
Die wellenhafte Auslenkung Ψ ist eine komplexwertige Funktion der drei Ortskoordinaten und der Zeit:
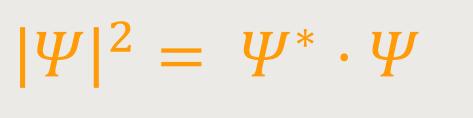
Diese Beziehung beschreibt die Wahrscheinlichkeitsdichte für das Auftreten des entsprechenden Teilchens an einer bestimmten Stelle im Raum.
Wichtig ist dabei, dass diese Wellenfunktionen stationäre Wellenfunktionen sind. Die ursprünglichen Vorstellungen, nämlich dass Elektronen um einen Atomkern kreisen, wie die Planeten um die Sonne, ist inzwischen ein altes und überholtes Bild. Man geht heute davon aus, dass die Elektronen nicht kreisen, weil sie sonst Energie abstrahlen würden. Es sind vermutlich vielmehr stationäre Zustände.
Anders würde es sich aber verhalten, wenn die Elektronen womöglich doch kreisen, allerdings ständig ihren Energiezustand wechseln würden. Wie ein solches Pulsieren möglich wäre und aussehen könnte, damit befasst sich der Bereich „Wirbelstrukturen”. Dort wird eine neue Theorie vorgestellt, die einige der noch ungelösten physikalischen Phänomene lösen könnte.
⇦ Kapitel Kapitel ⇨
