Wir werden uns in diesem Kapitel im Wesentlichen nur mit einigen Grundprinzipien
der Speziellen Relativitätsmechanik beschäftigen. Daneben gibt es
auch die „Allgemeine Relativitätsmechanik”, die sich in einer tensoriellen
Obwohl viele den Begriff Relativitätstheorie verwenden, sollte man vielmehr von einer „Relativitätsmechanik” sprechen, denn viele der modernen Experimente wären ohne die relativistischen Rechnungen gar nicht möglich. Insofern gibt es eine solide Grundlage für diese Überlegungen, genauso wie es bei der Newton'schen Mechanik der Fall ist. Beide lassen sich theoretisch darstellen sowie experimentell untersuchen und sind wichtige Modelle der Physik.
Das Prinzip der Relativität ist im Grunde nichts anderes, als eine Fortsetzung bzw. Erweiterung des Prinzips der Relativität der Mechanik. Dort ist es ebenfalls so, dass in allen Inertialsystemen die gleichen Gesetzte der Mechanik gelten. Und nun wurde das Prinzip eben auf alle Naturgesetze erweitert.
Im einem früheren Kapitel haben wir gesehen, dass sich eine Transformation von einem Inertialsystem in ein anderes Inertialsystem nicht so ohne weiteres in die Maxwell-Gleichungen einsetzen lässt. Es werden dann zusätzliche Terme in Erscheinung treten, die zwar nur eine relativ kleine Größe beinhalten, aber sie haben dennoch Auswirkung auf die Grundgleichungen.
Daher kam die Überlegung auf, ob es nicht doch einen absoluten Raum gibt, in welchem sich die elektromagnetischen Wellen, ähnlich wie es die mechanischen Wellen auch tun, in einem Trägermedium ausbreiten. Und ein solches Trägermedium müsste bezogen auf irgendein Bezugssystem in Ruhe sein, und das wäre dann wahrscheinlich der absolute Raum. So dachte man zumindest, bis das Michelson-Experiment das Gegenteil bewies.
Und damit wurde die Grundlage für das Prinzip der Konstanz der Lichtgeschwindigkeit gelegt. Nämlich, in allen unbeschleunigten Systemen (Inertialsystem) hat die Vakuum-Lichtgeschwindigkeit den gleichen Wert. Damit war die Überlegung bezüglich eines Lichtäthers hinfällig.
Grafik (wird später eingefügt)
Laut dem Prinzip der Relativität gelten in allen Inertialsystemen die gleichen
Naturgesetze. Das betrifft insbesondere auch die Maxwell-Gleichungen. Das sind
insbesondere Naturgesetze, die dazu dienen, das elektromagnetische Feld zu beschreiben.
Diese Gleichungen beinhalten Vektordifferentialoperatoren mit
 -Feldern
-Feldern -Feldern
-Feldern
Und wenn man die jeweiligen Beziehungen umformt, erhält man mit wenigen Schritten die
Wellengleichung, jeweils für das
 -Feld
-Feld -Feld
-Feld
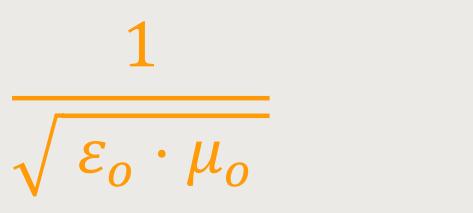
Und das gilt für jedes Inertialsystem. Das hat natürlich weitreichende Folgen. Somit hat die Lichtgeschwindigkeit im Vakuum in allen Inertialsystemen diesen Wert. Und das trifft auch auf die elektromagnetischen Wellen zu, die somit ein Wellenvorgang ohne Trägermedium sind.
Obige Prinzipien annullieren nicht nur den Ätherbegriff, sondern haben auch Auswirkungen auf den „Zeitbegriff”. Die Zeit ist zunächst einmal wie die Länge, die Geschwindigkeit und die Masse nur eine physikalische Messgröße. „Zeit” ist etwas, was man mit Uhren misst, so wie man „Längen” mit Maßstäben misst. Eine „Masse” wird mit einer Waage gemessen. Und so ist eine Uhr im Grunde nichts anderes, als ein periodisch ablaufender Schwingungsvorgang.
Insofern stellt sich die Frage, was es mit der Gleichzeitigkeit auf sich hat. Denn wenn es in jedem Inertialsystem so ist, dass sich das Licht in allen Richtungen gleichermaßen mit der Vakuum-Lichtgeschwindigkeit ausbreitet, können Lichtsignale zur Synchronisation von Uhren verwendet werden.
Grafik (wird später eingefügt)
Eine solche Synchronisation führt man durch, indem man zwei Uhren in einem gewissen Abstand aufstellt und genau in der Mitte ein Blitzlicht positioniert. Wenn der Lichtblitz aufleuchtet, laufen die Lichtsignale zu den beiden Uhren hin und die Sensoren empfangen einen Impuls, aufgrund dessen die Uhren zu laufen beginnen.
Die Definition der Gleichzeitigkeit lautet:
Ereignisse in einem Inertialsystem sind gleichzeitig, wenn sie von
Lichtsignalen ausgelöst werden, die zugleich von „einer” Quelle ausgehen.
Grafik (wird später eingefügt)
Der Begriff der „Gleichzeitigkeit” ist kein universeller Begriff, sondern ist gebunden an das jeweils betrachtete Inertialsystem. Und damit muss die Annahme einer universellen Zeit aufgegeben werden.
Grafik (wird später eingefügt)
„Gleichzeitigkeit” ist jeweils nur für ein bestimmtes Bezugssystem gültig. Aus Sicht eines Beobachters gilt die Gleichzeitigkeit nur für das Inertialsystem, in welchem sich der Beobachter befindet.
Grafik (wird später eingefügt)
Daraus ergibt sich eine Konsequenz, die zu unserer Alltagserfahrung im Widerspruch steht. Nämlich, dass Ereignisse die im gleichen System stattfinden und zur gleichen Zeit, aber mit einem gewissen Abstand voneinander, aus Sicht eines anderen Systems nicht mehr zur gleichen Zeit stattfinden.
Das klingt äußerst merkwürdig. Würde man jetzt die Begriffe Ort und Zeit einfach gegeneinander austauschen, ergäbe sich etwas, was mit unserer Alltagserfahrung wieder im Einklang steht. Nämlich, dass Ereignisse die im gleichen System stattfinden, und am gleichen Ort, aber zu verschiedenen Zeiten, aus Sicht eines anderen Systems an verschiedenen Orten stattfinden.
Um letzteres zu veranschaulichen, kann man sich gedanklich einen Zug vorstellen, der gleichmäßig und geradlinig zwischen zwei Orten unterwegs ist. Nehmen wir an, man säße im Speisewagen und äße am gleichen Ort, aber zu verschiedenen Zeiten ein mehrgängiges Menü am selben Tisch. Von außen betrachtet ein Beobachter aus Sicht eines anderen Systems das Geschehen. Der Beobachter sieht, dass die Vorspeise vielleicht in der Nähe der Ortes XY serviert wird, wogegen die Nachspeise erst am Ort YZ serviert wird.
Deshalb findet auch das, was die Relativitäts-Mechanik ausdrückt, obwohl es sich zunächst merkwürdig anhört, durchaus statt, nur halt bei Geschwindigkeiten, die sich in der Nähe der Lichtgeschwindigkeit bewegen.
Die gleiche Merkwürdigkeit lässt sich auch auf Uhren übertragen. Denn wenn man eine Uhr relativ zu einem Bezugssystem bewegt, beobachtet man einen anderen Uhrengang. Allein durch die Bewegung einer Uhr ändert sich schon ihre Periodendauer. Und wenn sich die Periodendauer aus der Sicht eines anderen Beobachters ändert, dann hat sich letztlich die Zeit, die mit der Uhr gemessen wird, verändert.
Wichtiger Hinweis:
Diese Überlegungen gelten aber nur für den Spezialfall eines
unbewegten Bezugssystems, deshalb auch der Begriff der „Speziellen
Relativitätstheorie”. Um der Realität Rechnung zu tragen müssen auch
bewegte Systeme mit einbezogen werden, was mit der „Allgemeinen
Relativitätstheorie” berücksichtig wird.
⇦ Kapitel Kapitel ⇨
