Eine nach wie vor heiß diskutierte Frage unter den Astro­physikern lautet: Ist unser Universum flach oder gekrümmt?
Viele, die etwas auf sich halten, sprechen sich für ein flaches Universum aus. Dass sich aus kosmo­logischer Sicht unser Universum ausdehnt, muss wohl niemand anzweifeln. Wenn­gleich der Urknall viel­leicht doch nicht exakt so statt­gefunden hat, wie man ihn sich gegen­wärtig vorstellt. Denn mit zuneh­mendem Erkenntnis­gewinn tauchen Probleme auf, die dieses Modell zumindest an den Grund­festen rütteln lässt.

Da gibt es zum einen das „Horizontproblem”.

Bei der Frage­stellung nach dem Aufbau unseres Universums hatte Alexander Friedmann seiner­zeit gefordert, dass es homogen und isotrop sein muss. Dies war unabdingbar für die nach ihm benann­ten Gleichungen. Doch letzt­lich waren die Aufnahmen der kosmi­schen Hinter­grund­strahlung ausschlag­gebend für diese Annahme. Laut theore­tischer Berech­nungen muss es dem Licht etwa 380 000 Jahre nach dem Urknall gelungen sein, sich aus dem anfäng­lichen Plasma zu entkoppeln. Aller­dings zeigt die Aufnahme dieser Hinter­grund­strahlung etwas Bemerkens­wertes. Sie ist nahezu gleich­förmig, und die Temperatur­abweichungen betragen gerade mal 10^-5 Kelvin.

Daraus ergibt sich folgendes Problem: Wie können Bereiche, die heute viel weiter vonein­ander entfernt sind, als das Licht Zeit gehabt hätte, diese Entfer­nungen zu über­winden? Denn wenn das Universum seit einer „endlichen Zeit” existiert, dann expandiert es auch in einem „endlichen Bereich”, in welchem es Wechsel­wirkungen geben muss. Und trotz­dem herrscht im gesamten Universum eine mittlere Temperatur von 2,725 Kelvin.

Daran schließt sich die Frage an, wenn das Universum so homogen ist, warum gibt es dann über­haupt Schwankungen?

Hierzu könnte man sich zwei gleich entfernte Punkte zu einem Beobachter vorstellen, zwischen denen noch Wechsel­wirkungen möglich sind. Idealer­weise wäre das 380 000 Jahre nach dem Urknall gewesen, zu einer Zeit, in der das Licht mittler­weile die beiden Punkte hätte erreichen können. Genauso wären umge­kehrt noch Infor­mationen von den beiden Punkten zum Beobachter gelangt. Das wäre dann insgesamt die Sphäre, in der Wechsel­wirkungen hätten statt­finden können.

Nun haben ja beide Punkte ihrer­seits einen Horizont, die sich beim Beobachter treffen. Die beiden Horizonte über­schneiden sich nicht, weil wir nur den gegen­wärtigen Zeit­punkt betrachten. Selbst wenn man in die Zeit zurück­schaut, wären die Punkte zwar näher beieinander gewesen, aber die jewei­ligen Horizonte hätten noch nicht bis an den Beobachter heran gereicht, weil ja die Expansion des Universums berück­sichtigt werden muss. Alles hängt nämlich vom sogenannten Skalen­faktor a ab, der mit c · t einhergeht. Je nach Entwicklungs­phase des Universums geht dieser Faktor auch mit √t oder auch mit t^2/3 einher. Und das entspricht einer schwächeren Expansion als zum heutigen Zeitpunkt. Somit schrumpfen die Horizonte rück­blickend in früheren Zeit­perioden effektiver.

Diagramm (wird später eingefügt Zeit) t und Skalenfaktor a

In einem Diagramm würde der Horizont, darge­stellt durch ct, propor­tional verlaufen. Der Expansions­verlauf des Universums dagegen steigt zunächst an und fällt im weiteren Verlauf stärker ab. Der Kurven­verlauf beschreibt zugleich den Abstand zwischen den zuvor betrach­teten zwei Punkten A, B. Zwischen den beiden Bezie­hungen gibt es einen charakte­ristischen Schnitt­punkt. Als Inter­pretation lässt sich fest­stellen: In diesem Fall ist der Horizont größer und wächst stärker als der Abstand zwischen den beiden Punkten.

Wenn es aber keine kausalen Wechsel­wirkungen gibt, dann gibt es in der Vergangen­heit erst recht keine Bedingungen, die dies zuließen, denn der Skalen­faktor würde ober­halb des Horizonts liegen. Das ist die Krux an einem anfänglich schnell und später langsam expan­dierenden Universum.

Alternativ könnte man ein Diagramm betrachten, mit einem Horizont, der zwar proportional gleich verläuft, aber dieses Mal mit einem exponen­tiell anstei­genden Skalen­faktor der Expansion. Nun käme es in der Vergangen­heit zu einer Phase, in welcher der Horizont der beiden Punkte größer ist, als die Entfernung zwischen den beiden Punkten. Da es zu Über­schneidungen beider Horizonte kommt, wären kausale Wechsel­wirkungen möglich gewesen. Dieses Szenario steht aber im Wider­spruch zur gängigen Vorstellung des Urknall­modells.

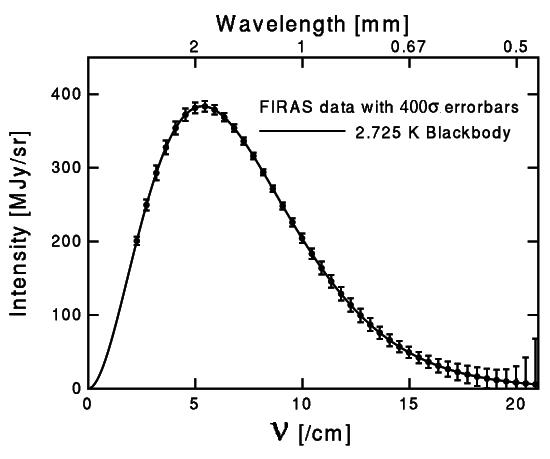
Abb. 1: Spektrum der Hintergrundstrahlung

Des Weiteren sind die Dichte­fluktuationen skalen­abhängig, was letzt­lich zu dem Flachheits­problem führt. Dieses Problem begründet sich in der Anfangs­konstellation, welche eine kritische Dichte nahe an dem gemessenen Wert unserer heutigen Dichte im Universum festlegt. Wir weichen heute „nur” 1% von der kritischen Dichte ab.

Wenn man die im Universum vorhandene Dichte ins Verhältnis setzt zur kritischen Dichte, erhält man einen Wert von 1,01. Manche fragen sich zu Recht, worin liegt das Problem? Das ist doch nahe an Eins, eine fast perfekt kritische Dichte, also spricht doch alles dafür, dass unser Universum flach ist.

Schaut man sich aller­dings die Friedmann­gleichung genauer an, erkennt man besser, worin das eigentliche Problem liegt.

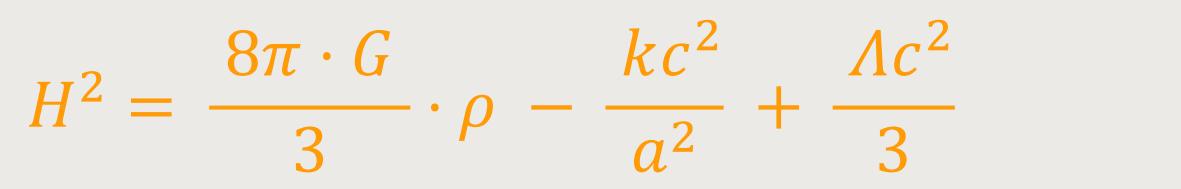
H   ist die Hubble-Konstante
G   ist die Gravitationskonstante
ρ   ist die Dichte
a   Skalenfaktor
k   Krümmungsparameter (0, +1, -1)

Schauen wir uns zunächst nur einen Teil der Gleichung an:

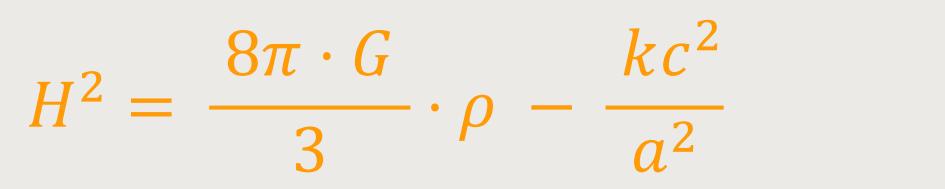
Diese Beziehung lässt sich auch umstellen, unter der Annahme dass die Krümmung konstant ist:

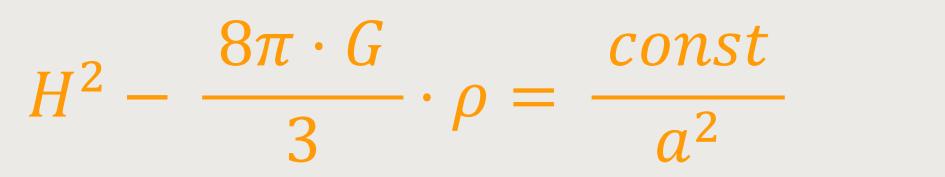
Wenn man nun auf der linken Seite die Hubble-Konstante ausklammert, erhält man:

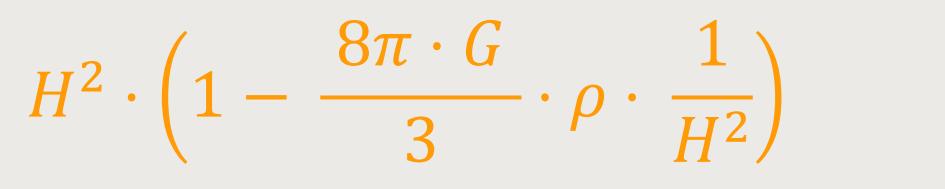
Gehen wir noch einen Schritt weiter. Die kritische Dichte lässt sich beschreiben als:

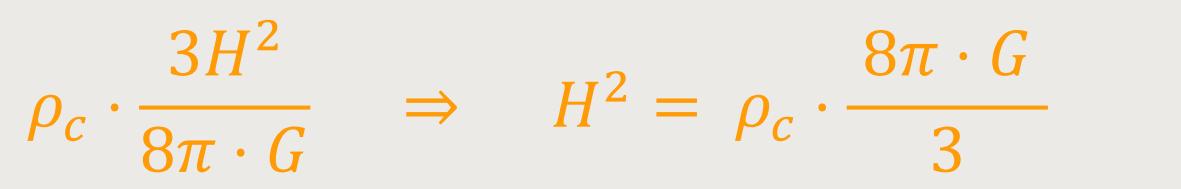
Durch Einsetzen und Kürzen erhalten wir:

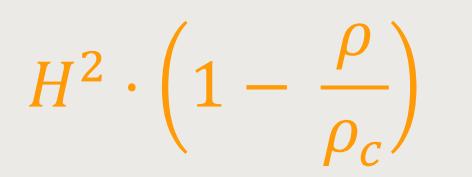
Und dieses Verhältnis ρ/ρ_c wird allgemein mit Ω bezeichnet und kenn­zeichnet die Flachheit im Universum. Daraus ergibt sich jetzt folgende Gleichung:

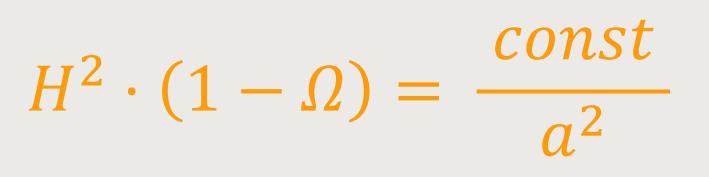
Eine andere Schreibweise für die Hubble-Konstante ist auch:

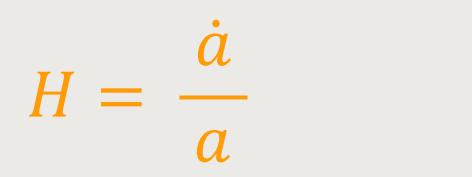
Durch erneutes Einsetzen und Kürzen erhalten wir abschließend:

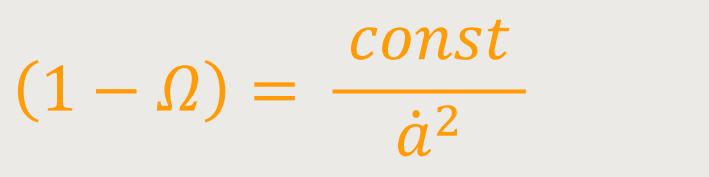
Diese Beziehung besagt jetzt nichts anderes, als dass das Verhäl­tnis der Dichte unseres Universums zur kritischen Dichte, bezogen auf die Größe Eins, abhängig ist von einem im Nenner. Mit anderen Worten, wenn sich der Skalen­faktor schnell ändert, wird der Nenner sehr groß und damit der Gesamt­ausdruck sehr klein, und letzt­lich auch die Abweichung der Dichte zur kritischen Dichte. Insofern liegen wir damit nahe bei Eins. Daraus folgt, je größer unser Universum, desto flacher erscheint es uns.

So weit so gut, doch daraus ergibt sich das eigent­liche Problem. Denn wenn wir aus heutiger Sicht ein flaches Universum haben, dann wäre das Universum in der Frühphase, bei einer Zeit­spanne von 13,8 Mrd. Jahren, um ein Viel­faches flacher gewesen.

Denn wenn man den obigen Wert von 1,01 für Ω beispiels­weise 1 Sekunde nach dem Urknall ansetzt, dann würde dieser Wert bereits nach einer Minute bei 2,... liegen. Doch mit diesem Wert würde unser Universum wieder in sich zusammen­stürzen.

Damit man dennoch den aktuellen Wert von 1,01 zugrunde legen kann, müsste in der Frühphase des Universums ein um viele Größen­ordnungen abweichender Wert von 10^-16 angesetzt werden. Und je näher man an die Plank-Zeit heranrückt, also die kleinste plausible Zeit von 10^-44 Sekunden, wird die Fein­abstimmung immer abstruser.

Vielleicht liegt das Problem aber auch nur darin begründet, dass man am Anfang von einer Singula­rität ausgeht. Des Weiteren geht man davon aus, dass im Anschluss eine inflationäre Phase statt­gefunden haben muss, die das Universum exponen­tiell aufge­bläht hat. Das ist aus Sicht der Urknall­befür­worter zwar ein denkbares Szenario.

Was wäre aber, wenn wir am Anfang nicht von einer Singula­rität ausgehen, sondern bereits von einer extrem großen Ausdehnung mit einem gigantischen Quer­schnitt, der sich zunächst exponentiell aufbläht, ja womöglich sogar hyperbolisch, quasi wie bei einem Potential­topf und anschließend wieder exponentiell bzw. hyperbolisch verdichtet. Dann hätten wir ein zyklisches bzw. pulsierendes Universum, in welchem sich der Wert für Ω immer nahe bei Eins bewegen wird, mal leicht oberhalb und mal leicht unterhalb. Damit wäre auch auf einen Schlag das Horizont­problem gelöst. Wie das im Einzelnen aussehen könnte, wird später anschaulich beschrieben.

Doch in diesem Zusammen­hang stellt sich auch die Frage nach den Monopolen. Denn in den vereinheit­lichten Theorien für die Früh­phase des Universums, gibt es auch die Über­legung, dass es nicht nur Ladungs­träger für elek­trische Ladungen gibt, sondern auch für Magne­tismus. Diese nennt man auch „magne­tische Mono­pole” mit einer Masse von 10¹⁶ Protonen-Massen. Bisher hat man diese aller­dings nicht entdeckt, obwohl man sich vorstellt, dass ihre Verteilung 1/m³ betragen könnte.

Wenn es in der Früh­phase einen Mecha­nismus gegeben hätte, der exponen­tiell alles auseinander getrieben hat, dann müsste er die Anwesen­heit dieser Monopole so sehr „verdünnen”, dass man bisher keine nach­weisen konnte. Aber warum ist man so scharf auf diese magne­tischen Monopole?

Von Paul Dirac stammt die Speku­lation, es könne den magne­tischen Mono­pol als Elementar­teilchen geben, welches das magne­tische Gegen­stück zum Elektron wäre. Das Vorhanden­sein dieser Mono­pole hätte unter anderem zwei Vorteile:

Die merkwürdige Asymmetrie zwischen den sonst so ähnlichen Erscheinungen des Magne­tismus und der Elektri­zität, wie sie sich in den Maxwell-Gleichungen darstellen, wäre behoben.

Des Weiteren wäre erklärbar, warum die elek­trische Ladung stets nur „gequantelt”, d. h. in ganz­zahligen Viel­fachen der Elementar­ladung auftritt.

Und letztlich möchte man auf diese Weise magne­tische Ladungen trans­portieren. Was ein faszinie­rendes Pendant zur Elektri­zität wäre. Das sind alles Über­legungen hin zu einem vereinheit­lichenden Modell, wozu auch die String­theorie gehört.

⇦ Kapitel Kapitel ⇨