Unter der „Nullpunkts­energie”, die auch gerne Vakuum­energie genannt wird, versteht man die Differenz zwischen der Energie, die ein quanten­mechanisches System im Grund­zustand besitzt und dem Energie­minimum, welches das System hätte, wenn man es klassisch beschreiben würde. Bezogen auf thermo­dynamische Systeme, welche die Energie mit ihrer Umgebung austauschen, ist die Nullpunkts­energie gleich der Energie des Systems am absoluten Temperatur­nullpunkt.

Abb. 1: Potentialfunktion des harmonischen Oszillators (rot). Ein Teilchen in diesem Potential kann nur bestimmte Energien annehmen (blau). Die kleinstmögliche dieser Energien liegt oberhalb des Potentialminimums.

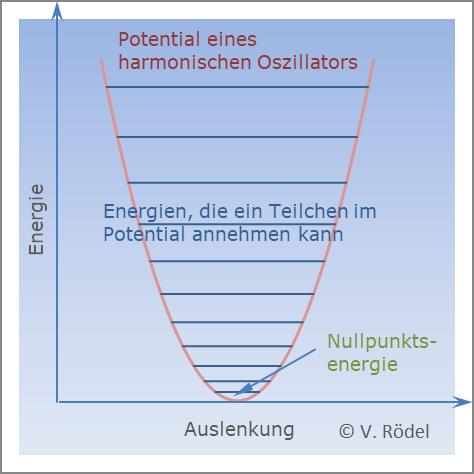
Die Nullpunkts­energie wird üblicher­weise anhand von 1-dimen­sionalen Systemen eines Teil­chens in einem Potential einge­führt. In der klassischen Physik ist der energie­ärmste Zustand derjenige, in welchem das Teil­chen im Potential­minimum ruht. In der Quanten­mechanik dagegen kann die kleinste erreich­bare Energie über dem Wert des Potential­minimums liegen. In einem quanten­mechanischen System kann der Energie­eigen­zustand ermittelt werden, wenn seine Energie einen definierten Wert hat.

Alternativ kann man dieses Resultat durch Verwenden der Unschär­ferelation erhalten.^[1] Eine endliche Orts­unschärfe, wie sie z. B. bei gebundenen Zuständen vorliegt, verlangt im Allge­meinen eine Impuls­unschärfe größer als Null. Daher können der Impuls und die kinetische Energie nicht exakt Null sein. Da die kinetische Energie nicht negativ werden kann, ergibt sich daraus:

Daher muss die Gesamt­energie, sprich die Summe aus poten­tieller Energie und kinetischer Energie, größer sein als das Minimum der potentiellen Energie:

Das Standard­beispiel für die Null­punkts­energie ist der quanten­mechanische harmonische Oszillator. Seine potentielle Energie wird wie folgt definiert:

m   ist die Masse
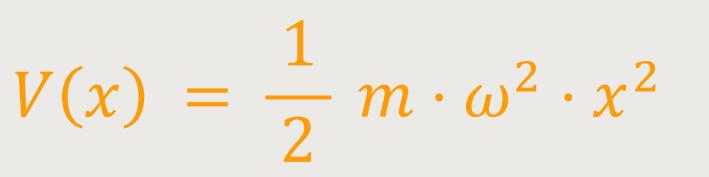
ω   ist die Kreisfrequenz
x    ist die Auslenkung

Dieses Potential hat ein Minimum bei V(x) = 1/2 = 0.
Die möglichen Energien des quanten­mechanischen harmonischen Oszillators sind nicht konti­nuierlich, sondern können nur einen der folgenden Werte annehmen:

n   ist eine positive ganze Zahl
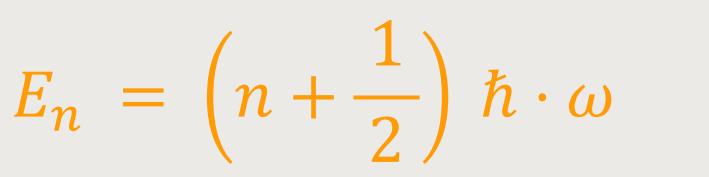
ℏ   ist das reduzierte plancksche Wirkungsquantum

Auch im energetisch niedrigsten Zustand, dem Grund­zustand mit n = 0, existiert somit eine von Null abweichende Energie:

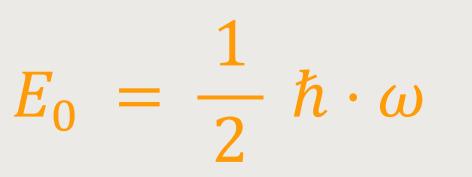
Im klassischen Fall ist der Zustand niedrigster Energie der, bei dem das Teilchen am Ort x = 0 ruht, also p = 0. In der Quanten­mechanik verbietet aber die Unschärfe­relation, dass beide Größen in Abhängig­keit von Ort und Impuls exakt gemessen werden können. Denn je genauer der Ort bekannt ist, desto ungenauer kennt man den Impuls und umgekehrt. Deswegen ergibt sich die Null­punkts­energie als Mittel­wert dieser Schwankungen.

Als eine der ersten sicheren Beobach­tungen der Null­punkts­energie massiver Teil­chen gilt, dass flüssiges Helium unter Normal­druck bis zu den tiefsten Tempera­turen nahe dem absoluten Null­punkt nicht fest wird.^[2] Schon seit langem ist der von der Null­punkts­energie der Molekül­schwingung verursachte Unter­schied der Bindungs­energie bekannt, zwischen normalem Wasser­stoff H_₂ und dem aus zwei Deuterium-Atomen bestehenden D_₂.^[3]

Als indirekter Beweis für die Null­punkts­energie des elektro­magne­tischen Feldes werden die damit zusammen­hängenden Vakuum­fluktua­tionen heran­gezogen, mit denen der Casimir-Effekt und die Lamb-Verschiebung erklärt werden können. Es ist jedoch möglich, den Casimir-Effekt auch ohne den Rück­griff auf diese Null­punkts­energie herzuleiten.^[4]

Die Lamb-Verschiebung ist ein Phänomen in einer wechsel­wirkenden Quanten­feld­theorie, welches genau genommen nicht auf die Null­punkts­energie zurück­geführt werden kann. Die Diskrepanz entsteht dadurch, dass die Lamb-Verschiebung als Folge virtueller Teilchen-Antiteilchen-Paarbildung erklärt wird, welche im Feld eines geladenen Teil­chens auftritt und eigent­lich nicht aus dem Vakuum heraus stattfindet.

Die Vakuum­energie gilt als ein mög­licher Kandidat für die Dunkle Energie, welche in der Kosmologie eine Erklärung für die beobach­tete beschleunigte Expansion des Universums bieten soll. Die Menge der Vakuum­energie stellt in diesem Zusammen­hang aller­dings eines der größten Probleme der modernen Physik dar. Denn die experimen­tellen Werte weichen von den theore­tisch vorher­gesagten Werten für die Vakuum­energie als Dunkle Energie extrem ab.

Aufgrund von astro­nomischen Beobach­tungen wird die Energie­dichte des Vakuums auf einen Wert der Größen­ordnung 10^-9 bis 10^-11 J/m³ geschätzt,^[5][6][7] sie ist damit etwa um den Faktor 10¹²⁰ niedriger als in den theore­tischen Berech­nungen der Quanten­physik.

Anfang des letzten Jahrhunderts vertrat man noch die Auffassung, dass im leeren Raum ein Äther als Medium für die Fort­pflanzung von Wellen und für die Bewegung von Körpern verant­wortlich sei. Dann vertrat man in der klassischen Physik die Vorstellung eines weder Materie noch irgendeine Form von Energie enthaltenden Vakuums.

Doch schon das von Max Planck im Jahr 1911 gefundene Strahlungs­gesetz seiner „zweiten Theorie” legte eine Null­punkts­energie des elektro­magne­tischen Feldes im Vakuum nahe, da eine von der Tempe­ratur unab­hängige Größe ½ hν auftrat. Aller­dings maß Planck dem zunächst keine Bedeutung hinsicht­lich eines experimen­tellen Nach­weises zu.^[8][9]

Bei ähnlichen Über­legungen gelangten Albert Einstein und Otto Stern 1913 zu dem Schluss, dass die Null­punkts­fluktua­tionen des elektro­magne­tischen Feldes am absoluten Null­punkt der Temperatur bei hν lägen.^[9]

Aufbauend auf den Arbeiten Plancks schlug Walther Nernst zum einen Null­punkts­fluktuationen für das elektro­magnetische Feld um den Wert ½ hν vor^[11] und zum anderen, dass das gesamte Universum von Null­punkts­energie erfüllt sei.^[10]

Im Jahr 1927 formulierte Werner Heisenberg seine Unschärfe­relation, die als Grund­lage der Null­punkts­energie in jedem quanten­mecha­nischen System gilt.^[11]

Georges Lemaître, der wegweisende theore­tische Arbeiten zum Urknall und zur Expansion des Universums geleistet hatte, fand 1934 eine Über­ein­stimmung der Vakuum­energie mit der kosmo­logischen Konstanten Einsteins (1917). Aller­dings hatte Einstein später die nacht­rägliche Einführung seiner Konstante als die „größte Eselei” seines Lebens bezeichnet.^[12]

Bei einer Unter­suchung der Van-der-Waals-Kräfte in Kolloid­lösungen verwendete Hendrik Casimir zusammen mit Dirk Polder 1947 einen quanten­mechanischen Ansatz, welcher zu einer Diskussion mit Niels Bohr führte. Bohr äußerte hierzu, „das muss etwas mit Null­punkts­fluktua­tionen zu tun haben”.^[13]

Casimir ging der Idee nach, dass die Anziehung zwischen neutralen Atomen viel­leicht nur auf Vakuum­fluktua­tionen beruhen könne und veröffent­lichte 1948 seine grund­legende Arbeit über die Anziehung zwischen zwei perfekt leitenden Platten.^[14] Darin beschrieb er eine theore­tische Versuchs­anordnung mit zwei Metall­platten im Vakuum, die sich seinen Berech­nungen nach aufgrund der Vakuum­energie des elektro­magnetischen Quanten­feldes anziehen sollten. Dieser Effekt wird allgemein als „Casimir-Effekt” bezeichnet.

Erste entsprechende Versuche zum Nachweis der Casimir­kraft im Vakuum wurden 1958 von Marcus Sparnaay durch­geführt,^[15] aller­dings mit einem Mess­fehler von etwa 100%.^[16] Allmäh­lich erreichten die Messungen der Casimir­kraft (Wert für zwei Spiegel von 1 cm² Fläche im Abstand 1 μm: 10^-7 N ^[13]) eine höhere Genauigkeit. Zum Beispiel betrug der Mess­fehler bei van Bloklands und Oveerbeeks 1978 durch­geführten Versuch „nur” noch 25% ^[17] und bei Steven Lamoreaux 1996 schließlich ansehnliche 5%.^[18]

In den letzten Jahren fand auch die kosmolo­gische Konstante, die in engem Bezug zur Krümmung der Raum­zeit steht, wieder mehr Beachtung, zumal sie nun als kleine positive Energie­dichte des Vakuums angesehen wird. Eine neuere Erklärung für die kosmo­logische Konstante liefert beispiels­weise ein zyklisches bzw. pulsierendes Universum, wie es auch auf dieser Website favorisiert wird.

Quellen

[1] F. Schwabl: Quantenmechanik, 6. Auflage, Kapitel 3.1.3.
[2] Nikolaus Barth: Festes Helium. In: Naturwissenschaften. Band 44, Nr. 24, 1957, S. 627-630, PDF.
[3] A. Balakrishnan, B. P. Stoicheff: The Dissociation Energy of Deuterium. In: Journal of molecular spectroscopy. Band 156, 1992, S. 517-518.
[4] R. L. Jaffe: The Casimir Effect and the Quantum Vacuum. In: Physical Review D. Band 72, 2005.
[5] J. Baez. What's the energy density of the vacuum?, 2006.
[6] S. M. Carroll: The Cosmological Constant.
[7] A. Tillemans. Platons Höhlengleichnis und die Vakuumenergie des Universums. In: wissenschaft.de. 19. August 2002.
[8] Max Planck: Eine neue Strahlungshypothese. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Band 13, 1911, S. 138-148.
[9] B. Haisch, A. Rueda und Y. Dobyns: Inertial mass and the quantum vacuum fields. In: Annalen der Physik. Band 10, 2000, S. 393-414.
[10] Walther Nernst: über einen Versuch von quantentheoretischen Betrachtungen zur Annahme stetiger Energieänderungen zurückzukehren. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Band 4, 1916, S. 83.
[11] Werner Heisenberg: über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. In: Zeitschrift für Physik. Band 43, 1927, S. 172-198.
[12] J.-P. Luminet: The Rise of Big Bang Models, from Myth to Theory and Observations. 2007.
[13] A. Lambrecht: Das Vakuum kommt zu Kräften. In: Physik in Unserer Zeit. Band 2, 2005, S. 85-91.
[14] Hendrik Casimir: On the attraction between two perfectly conducting plates. In: Proc. Con. Ned. Akad. van Wetensch. B51 (7), 1948, S. 793-796.
[15] M.J. Sparnaay: Measurements of attractive forces between flat plates. In: Physica. 24, 1958, S. 751.
[16] R. Onofrio: Casimir forces and non-Newtonian gravitation. In: New Journal of Physics. Band 8, 2006, S. 237.
[17] P. H. G. M van Blokland und J. T. G. Oveerbeek: The measurement of the van der Waals dispersion forces in the range 1.5 to 130 nm. In: Journal of the Chemical Society Faraday Transactions. Band I74, 1978, S. 2637.
[18] S. K. Lamoreaux: Demonstration of the Casimir force in the 0.6 to 6 μ range. Physical Review Letters. Band 78, Nr. 1, 1997, S. 5-8.

⇦ Kapitel Kapitel ⇨