Hinweis: In der klassischen Mechanik bleibt die Masse konstant. Die Einheit der Masse ist das kg. Die Einheit der Beschleu­nigung ist m/s /s also m/s². Daraus folgt:

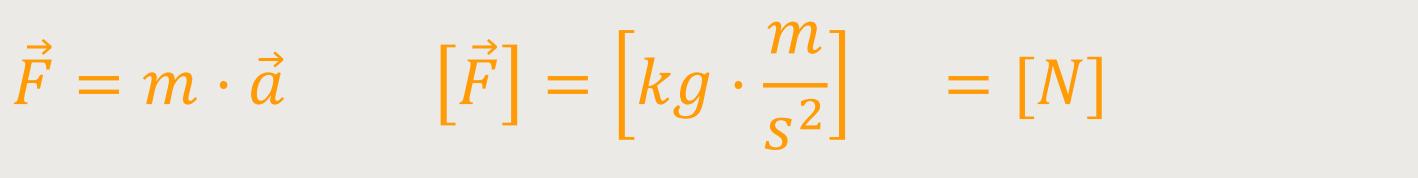
Bei einer Kraft von 1 N (Newton), wird einer Masse von 1 kg die Beschleu­nigung von 1m/s² zugeordnet.

Der Impuls ist ja definiert als:

Wenn auf eine bestimmte Masse eine doppelt so große Kraft wirkt, wird der Körper auch doppelt so groß beschleunigt.

Bei einer 1-dimensionalen Beschleu­nigung ergibt sich aus der Kinematik für die Bewegung:

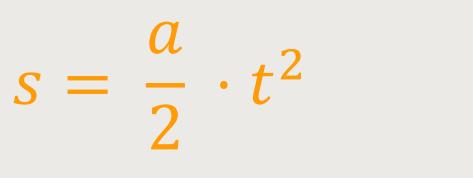
Die Beschleunigung wird demnach definiert als:

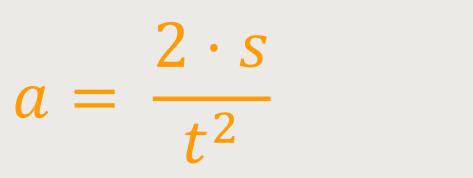
Wenn man zum Beispiel im Versuchsaufbau den gesamten Weg konstant hält s = const, dann wird die Beschleu­nigung bei einer gleich­förmig beschleunigten Bewegung proportional zu 1 /t² sein. Hierbei gehen wir von einer Anfangs­geschwindig­keit Null aus, und dass t das Zeitintervall ist.

Wie wir bereits gesehen haben, charakte­risiert die Masse die Träg­heit eines Körpers, sprich den Wider­stand den der Körper einer Beschleu­nigung seiner selbst entgegen­setzt.

Was passiert aber, wenn zwei Körper miteinander in Wechsel­wirkung stehen? Wenn sie sich also gegen­seitig in ihrer Bewegung beein­flussen? Entscheidend ist hierbei zu wissen, in welcher Art und Weise sie das tun werden.

Wenn zum Beispiel auf zwei gleich große Massen nur innere Kräfte wirken, dann werden diese in entgegen­gesetzte Rich­tungen gleich stark beschleunigt. Das heißt, es wirken betrags­mäßig die gleichen Kräfte, die aber richtungs­mäßig entgegen­gesetzt gerichtet sind.

Das 3. Newton-Axiom bezeichnet man auch als „Wechsel­wirkungs­satz” bzw. „Reaktionssatz”:

Für Kräfte auf zwei wechsel­wirkende Körper gilt, dass diese beiden entgegen­gesetzt gleich sind.

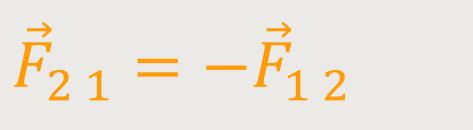
Obige Definition trifft dann zu, wenn zwei wechsel­wirkende Kräfte in der gleichen Wirkungs­linie verlaufen.

Welche Schluss­folgerungen können wir jetzt aus den drei Newton-Axiomen ziehen?

Wie wir gesehen haben sind Kräfte die Ursachen von „Impuls­änderungen”.

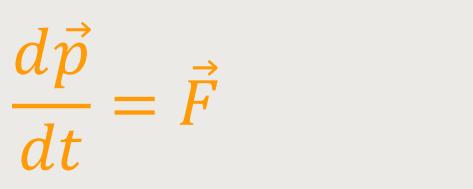
Daraus ergeben sich in der Mechanik weitere „Erhaltungs­sätze”.

Kräfte sind Ursachen von Impuls­änderungen. Wenn die äußere Kraft verschwindet, ist der Impuls 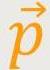konstant. Das nennt man den „Impuls­erhaltungs­satz”. Diese Gesetz­mäßigkeit gilt auch dann, wenn man nicht nur einen einzelnen Massen­punkt, sondern ein System von Massen­punkten betrachtet. Also Massen­punkte, die auch mit­einander wechsel­wirken können, bzw. wo äußere Kräfte wirken.

Daraus ergibt sich, dass der Gesamt­impuls, also die Summe aller Einzel­impulse, auch konstant bleibt. Das ist insbesondere dann der Fall, wenn die Summe aller äußeren Kräfte auf diese Körper gleich Null ist. Nichts desto trotz können innere Kräfte, also Wechsel­wirkungen zwischen den Teilchen, durchaus dabei vorhanden sein. Dieser Impuls­erhaltungs­satz hat mehrere Anwendungen, besonders bei Stoß­vorgängen und Streu­vorgängen.

Darüber hinaus gibt es auch den „Dreh­impuls”, der mit dem Impuls als solches zusammen­hängt. Der Dreh­impuls ist nichts anderes, als das vektorielle Produkt des Orts­vektors und des Impuls­vektors eines Teilchens:

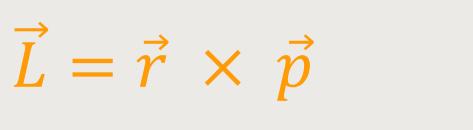
So wie aus dem Impuls der Dreh­impuls wird, so wird aus der Kraft das „Drehmoment”:

Die Winkelgeschwindig­keit hatten wir ja bereits schon betrachtet. Lässt sich auch eine entsprechende Beziehung zwischen dem Drehimpuls und der Winkel­geschwindig­keit 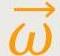herstellen?

Wenn wir uns im weiteren Verlauf mit der Bewegung von starren Körpern auseinander­setzten, werden wir sehen, dass der Dreh­impuls nicht immer parallel zu 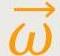ist. In einem solchen Fall hat man es mit sogenannten „Tensoren” zu tun. Dann lässt sich die Beziehung nicht mehr durch einen Skalar darstellen, sondern nur durch einen „Trägheits­tensor”. Die Masse ist charakte­ristisch für die Träg­heit linearer Bewegungen, während der Trägheits­tensor charakte­ristisch ist für die Träg­heit bei Dreh­bewegungen. Doch dazu später mehr.

Man kann diesen Drehimpuls auch nach der Zeit ableiten:

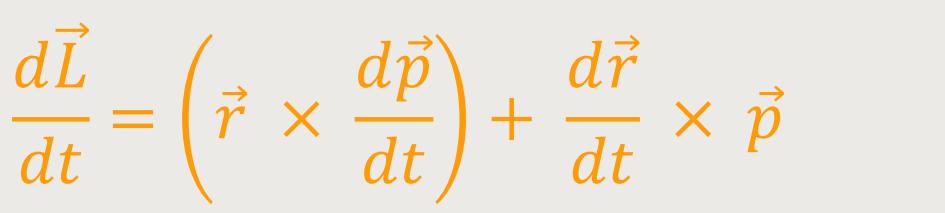
Der zweite Term ist immer gleich Null. Und wenn 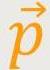d/dt = ist, erhält man den Drehimpulserhaltungssatz:

Wir haben hier eine ganz analoge Situation wie beim 2. Newton-Axiom.

Wenn das äußere Drehmoment verschwindet bzw. gleich Null ist, dann wird der Drehimpuls „konstant” sein.

⇦ Kapitel Kapitel ⇨