Im Allgemeinen ist an handels­üblichen Verbrauchern immer vermerkt, wie viel Leistung (Watt) ein elektrisches Gerät hat und ent­sprechend verbraucht. Es geht also darum, dass wir einen Leiter betrachten, an dessen Enden eine Spannung angelegt wird. Wir erinnern uns, die Spannung zwischen zwei Punkten in einem elektrischen Feld ist die Arbeit, die von diesem Feld verrichtet wird, wenn sich eine Ladung von dem einen Punkt zu dem anderen Punkt bewegt. Demnach ist Spannung gleich­bedeutend mit der Arbeit pro Ladungseinheit, oder bezogen auf die Arbeit gilt:

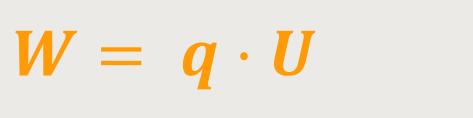
Ist diesem Fall entspricht die elektrische Leistung der Arbeit pro Zeiteinheit.

Wenn man also einen Ladungs­träger mit einer Ladung q in ein elektrisches Feld bringt, bei dem zwischen zwei Punkten eine Spannung U anliegt, wird der Ladungs­träger entsprechend beschleunigt. Denn es wirkt ununter­brochen eine Kraft auf ihn. Würden sich die Elektronen beispiels­weise im Vakuum befinden, dann würden sich diese sogar immer schneller bewegen. Das passiert verständ­licher­weise nicht, wenn sie sich durch einen Fest­körper hindurch bewegen.

An dieser Stelle wollen wir den Begriff „Elektronen­volt” einführen. Man verwendet die Einheit 1eV als eine inkohärente Energie­einheit. Das heißt, ein Elektronen­volt ist einfach diejenige Arbeit, die verrichtet wird, wenn ein Elektron, sprich eine Elementar­ladung, längs einer Spannung von 1 Volt beschleunigt wird, und sie durch nichts behindert wird. Die Ladung wird immer schneller und hat nachher eine entsprechend hohe kinetische Energie.

Die Elementarladung ist definiert als:

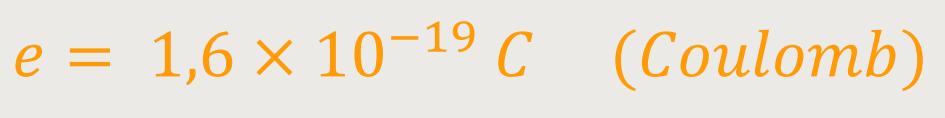
Insofern ist 1eV die Arbeit, die verrichtet wurde, wenn ein Elektron durch eine Spannung von 1 Volt hindurch beschleunigt wurde. Anschließend hat es dann eine ent­sprechende kinetische Energie.

Diese kinetischen Energien, die die Elektronen in ihrer Gesamt­heit in einem metal­lischen Festkörper erreichen können, ist viel geringer als im Vakuum. Der Grund dafür liegt in den anhaltenden Wechsel­wirkungen mit den Gitter­atomen. Und da die Gitter­atome thermische Energie besitzen, wird ständig Energie ausge­tauscht. Das heißt, die kinetische Energie der Elektronen selbst ist sehr gering. Das liegt daran, weil sie praktisch die ganze Energie, die sie aus dem elektrischen Feld auf­nehmen, gleich wieder als thermische Energie an die Gitter­atome abgeben, und dadurch den metal­lischen Fest­körper aufheizen.

Dementsprechend wird diese Energie, die von den Elektronen aufgenommen wird, voll­ständig vom Fest­körper als thermische Energie über­nommen. Daher kann man Rück­schlüsse daraus ziehen, wie groß diese Energie pro Zeit­einheit ist und man erhält damit die umgesetzte Leistung P bei konstanter Spannung:

Und wenn man die Spannung nicht ändert, bedeutet das:

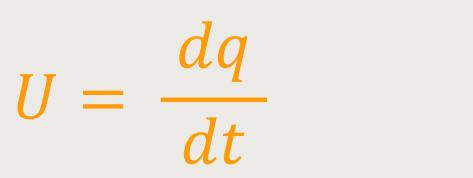
Das ist die Ladung, die pro Zeit­einheit durch den Quer­schnitt des Leiters hindurch­tritt.
Daher wird die elektrische Leistung definiert als:

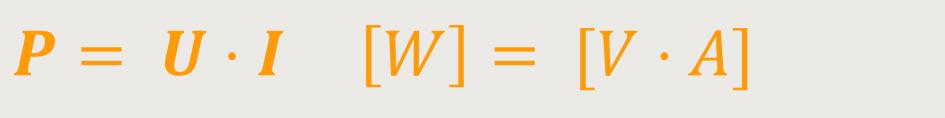
Die elektrische Strom­leistung ent­spricht der Spannung multi­pliziert mit der Strom­stärke. Man bezeichnet es auch als das „Joule'sche Gesetz”.

Zusammen mit dem Ohm'schen Gesetz lässt sich das in zwei unter­schiedlichen Weisen auf­schreiben. Zum einen kann man die Leistung in Abhängig­keit vom Strom betrachten. In diesem Fall wird in der Beziehung die Spannung U durch den Strom I ersetzt, und da U = I · R entspricht, bedeutet das:

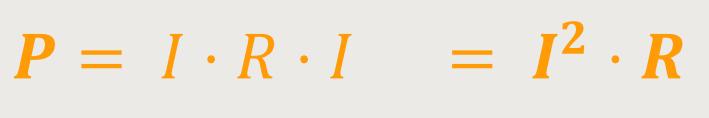
Anderseits kann es auch wichtig sein zu ermitteln, wie die Leistung ins­besondere von der Spannung abhängt. Dann ersetzt man den Strom I, und da I = U / R entspricht, bedeutet das wiederum:

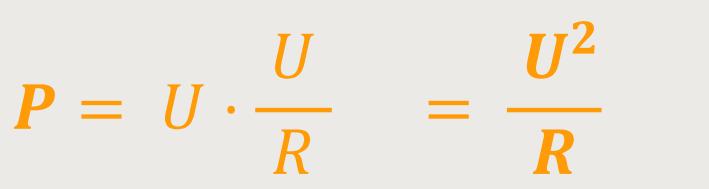
Diese beiden Bezie­hungen sind für die Praxis sehr wichtig, weil man daraus etwas Bedeutendes ablesen kann. Nämlich, wenn man den Strom konstant hält, wird die Leistung proportional zum Wider­stand sein. Und anderer­seits, wenn man die Spannung konstant hält, dann wird die umge­setzte Leistung proportional zu 1 / R sein. Das ergibt sich sofort aus diesen ganz einfachen Beziehungen, unter Berücksichtigung des Ohm'schen Gesetzes.

Ein klassisches Beispiel sind die Hoch­spannungs­fern­leitungen. Manch einer fragt sich, ob es keine andere Alternative zu diesem Strom­transport gibt. Mit obigen Beziehungen lässt sich das leicht beantworten.

Zunächst einmal: Man möchte eine Leistung über­tragen vom Kraftwerk bis zum Verbraucher. Das können im Regel­fall bis zu 400.000 Volt sein. Und diese Leistung entspricht dann U · I. Zweck­mäßiger­weise soll eine bestimmte Leistung über­tragen werden. Aber selbst wenn diese Hoch­spannungs­leitung noch so gut gebaut ist, hat sie einen gewissen material­abhängigen Innen­wider­stand. Insofern wird es zu einem Leistungs­verlust in dieser Leitung kommen. Der Verlust ist definiert als:

Worauf es jetzt ankommt, ist nicht das ΔP , sondern wie viel der relative Verlust beträgt. Das bedeutet, wie viel pro Gesamtleistung P geht verloren:

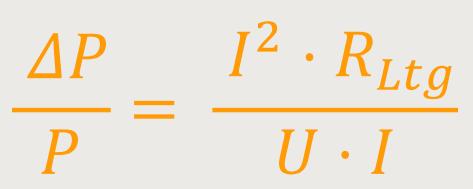
Wenn man jetzt die Beziehung kürzt, mit U erweitert und anschließend umformt, ergibt sich:

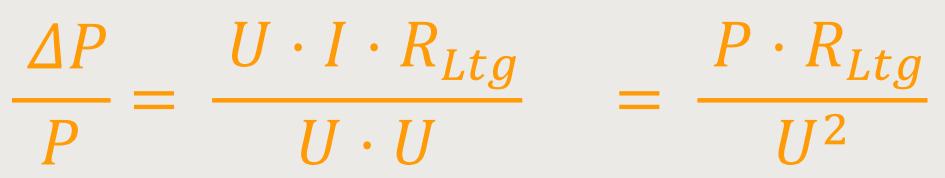
Warum geht man so vor? Es muss schließlich eine bestimmte voraus­gegebene Nennl­eistung über­tragen werden. Und zwar so, dass die Leistung P in dieser Beziehung eine konstante vorge­gebene Größe ist. Und das einzige, was verfügbar wäre, um etwas zu variieren, ist die Spannung U². Denn den Leitungs­widerstand kann man auf­grund der Leitungs­dimensionen nur bedingt beein­flussen. Bei Gleich­strom­kreisen kann man da auch nicht viel machen. Aber bei Wechsel­strom­kreisen lassen sich durch Trans­formatoren die Spannungen extrem herauf­setzen. Gleich um einen Faktor 1000.

Also, wenn wir zum Beispiel im Keller in einem Dreh­stromkreis einen Verbraucher von 400 Volt haben, beträgt die Hoch­spannungs­leitung 400.000 Volt. Wird jetzt aber die Spannung um das 1000fache erhöht, dann wird der relative Verlust bedingt durch das U² um einen Faktor 1000² = 10⁶ geringer. Genau das ist es, was man bei der Wahl der Energie­leitung mit berücksichtigen muss.

Insofern ist man gegen­wärtig schon zufrieden, wenn es einem gelingt, durch das Hoch­spannen mit Trans­formatoren bzw. mit den Umspann­werken den Verlust zu kompensieren. Also muss man die Hoch­spannungs­leitungen in Kauf nehmen, damit dieser Faktor 10⁶ nicht mehr ganz so zu Buche schlägt. Der Spannungs­abfall vom Umspann­werk zum Haus­halt ist klein genug, sodass dieser keine große Rolle spielt.

Wir werden die Mechanismen nach Aggregat­zuständen einteilen. Zuerst betrachten wir die Strom­leitung in Fest­körpern, wobei wir zwischen metal­lischen Leitern und Isolatoren unter­scheiden.

Bei den Fest­körpern interessieren uns in erster Linie die elektro­nischen Leiter. Das sind solche Leiter, bei denen der Energie­fluss durch die Elektronen erfolgt. Bei den Flüssig­keiten wären es dann die Ionen­leiter. Dort driften die Ionen quasi durch den Elektro­lyten hindurch. Bei den Gasen kann es sogar alles Mögliche sein, doch dazu später mehr.

Es gibt bei den metal­lischen Leitern die Eigen­schaft, dass mit zunehmender Temperatur auch der Wider­stand ansteigt. Man inter­pretiert das Verhalten so, dass mit höherer Temperatur die thermische Bewegung der Gitter­atome zunimmt.

Eine näherungs­weise empirische Formel für die Leit­fähig­keit lautet:

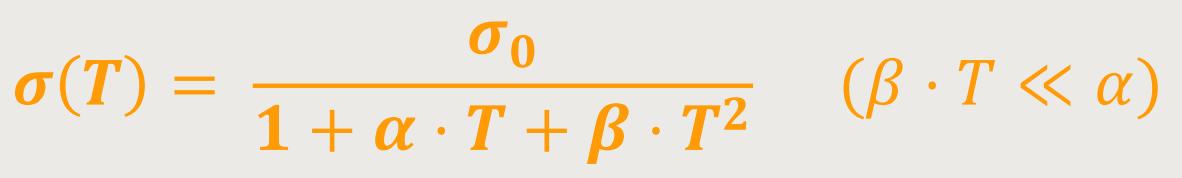
σ₀   ist die Leit­fähig­keits­größe (materialabhängig)

So erhält man die Leit­fähig­keit eines metal­lischen Körpers in Abhängig­keit von der Temperatur.

Wenn die Temperatur gegen Null geht, wird der Nenner gegen Eins gehen und das σ gegen σ_₀. Wir sprechen hier aller­dings noch nicht von Supra­leitung. Diese Formel beinhaltet die Eigen­schaft, dass es eine Grenz­leit­fähig­keit gibt, quasi einen geringsten Wider­stand. Dieser Wider­stand hat einen konstanten Wert, der im Wesent­lichen nicht mehr unter­schritten werden kann. Dieser Wert wiederum ist abhängig vom Material und dessen Rein­heit. Selbst kleine Verunreinigen können den Wert σ_₀ wesent­lich beeinflussen.

Die „Supra­leitung”, die auf der BCS-Theorie basiert, beruht auf der Existenz von sogenannten „Cooper-Paaren”. Bei niedrigen Temperaturen, bei denen die thermischen Bewegungen sehr gering werden, findet eine durch Korrelationen bedingte Anziehungs­kraft der Elektronen unter­einander statt. Und wenn diese Temperatur niedrig genug ist, können sich solche Cooper-Paare bilden.

Die Supra­leitung lässt sich im täglichen Gebrauch leider nicht effizient einsetzen. Dennoch gibt es einen anderen Quanteneffekt, der „Ferromagnetismus”, der bei den Metallen zu einer magnetischen Polarisier­barkeit beiträgt. Die Verän­derung basiert auch auf Quanten­korrelationen. Dort spielen aller­dings Temperaturen keine Rolle, weil der Effekt selbst bis 300°C zu beobachten ist. Erst wenn das Eisen rotglühend wird, verliert das Metall diese Eigenschaft. Die Supra­leitung dagegen kann das erst bei −100°C. Gäbe es den Effekt des Ferro­magnetismus nicht, könnte man keine leistungs­starken Generatoren und Trans­formatoren bauen.

Bei Metallen gehen die elektrische Leit­fähigkeit und die Wärme­leit­fähigkeit Hand in Hand. Wenn bei einem Metall die elektrische Leit­fähig­keit größer wird, steigt auch die Wärme­leitfähig­keit an:

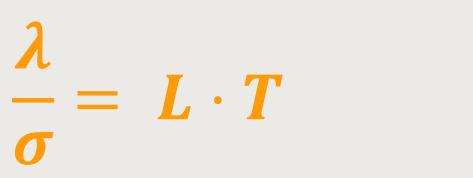
γ   ist die Wärmeleitfähigkeit
σ   ist die elektrische Leitfähigkeit
L   ist die Lorenzzahl

Das ist das Wiedemann-Franz-Gesetz.

Dieses Gesetz besagt, dass die freien Leitungs­elektronen auch zur Wärme­leit­fähigkeit beitragen.

Wir wollen noch kurz darauf eingehen, wie sich das auch „quanten­physikalisch” inter­pretieren lässt. Denn diese gravierenden Unter­schiede in der Leit­fähig­keit von Metallen und den Isolatoren lassen sich auf das sogenannte „Bänder­modell” zurück­führen.

Denn bei den Atomen sind die Kerne von Elektronen umgeben, die sich auf verschiedenen Energie­niveaus befinden. Das hat Konsequenzen auf die Eigen­schaften der verschiedenen Elemente und auf die Bindungs­mechanismen zwischen den Atomen. Letztlich hat es sogar Einfluss darauf, wie sich daraus Moleküle bilden können.

Wenn viele metal­lische Gitter­atome miteinander in Wechsel­wirkung stehen, werden die Elektronen auf den inneren Energie­niveaus wenig mit­einander zu tun haben. Aber in den äußeren Schalen kommen die Gitter­atome mit­einander in Kontakt. Und dann bilden sich Energie­bänder, die über ein Atom hinaus­gehen und sich über einen ganzen Verband von Gitter­atomen erstrecken. Inner­halb dieser Energie­bänder können sich die Elektronen verhältnis­mäßig frei bewegen. Wobei sich nur die Elektronen in den äußeren Schalen bewegen.

Da im Innern schon alle Energie­niveaus und Drehimpuls­niveaus besetzt sind, bauen sich die Schalen nach außen weiter auf. Und dadurch ergibt sich diese Elektronen­hüllen­struktur. Daran sieht man schon, dass es ein sogenanntes „Paulyverbot” für die Elektronen geben muss, sonst würden die alle Elektronen in die unterste Energie­ebene wandern. Insoweit werden die verschiedenen Energie­levels von unten nach oben aufgefüllt.

Bei genauerer Betrachtung stellt sich heraus, dass es bei Isolatoren oder Leitern in den äußeren Elektronen­hüllen noch ein letztes Energie­niveau gibt, welches voll­ständig mit Elektronen gefüllt ist. Diese Ebene wird auch als das „Valenz­band” bezeichnet. Die Elektronen in diesem Valenz­band sorgen insbesondere für die Bindungs­kräfte in den Gitteratomen.

Darüber hinaus gibt es noch ein weiter außen liegendes Energie­band, das entweder ganz leer oder teil­weise mit Elektronen gefüllt ist. Dieses bezeichnet man als das „Leit­fähigkeits­band”.

Grafik/Folie (wird später eingefügt)

Wie erwähnt, ist bei den Isolatoren das Valenz­band voll­ständig mit Elektronen gefüllt. Aufgrund der speziellen Struktur der Gitter­atome tritt ein großer Energie­sprung auf, und erst weiter außen gibt es das Leitungs­band. Im Leitungs­band selbst sind keine Elektronen enthalten. Nur in seltenen Fällen kann durch thermische Schwankungen und Tunnel­effekte ein Elektron auf das Leitungs­band überspringen.

Halbleiter sind so beschaffen, dass das „Leitungs­fähigkeits­band” näher an das Valenz­band heran­rückt. Dadurch wird die Wahrscheinlich­keit größer, dass ein Elektron auf das Leitungs­band über­springt. Und das bewirkt letzt­lich die Leit­fähig­keit des Materials. Auf­grund des nun fehlenden Elektrons entsteht im Valenz­band eine positive Lücke. Mit anderen Worten, aus diesem „Fermi-See” (Dirac-See) von lauter Fermionen wird quasi ein Elektron hinauf­gehoben, und in dem See entsteht diese positive Lücke. Weitere Elektronen können dann nach­rücken und die positive Lücke wandert ab. Die Elektronen, die sich nun im Leitungs­fähigkeits­band befinden, können sich dort frei bewegen. Dieses Konzept des Fermi-Sees wird verwendet, um positive Lücken gegen negative Elektronen zu beschreiben.

Aus der Relativitäts­mechanik weiß man, dass Energie und Masse miteinander äquivalent sind. Deshalb kann man auch damit rechnen, dass bei einer aus­reichenden Energie­menge, zum Beispiel in Form von elektro­magnetischer Strahlung, beispiels­weise Gamma­strahlung, sich die Massen von zwei neuen Teilchen bilden. Diese Teilchen bilden sich nach heutigem Verständnis aus einem Meer von Nichts, dem sogenannten „Dirac-See”. Und wenn dann durch diese hoch­frequente Energie ein Elektron heraus­gehoben wird, bleibt unten eine positive Lücke übrig. Und das bezeichnet man als Positron. Soviel zur Idee von der Paarbildung.

Grafik/Folie (wird später eingefügt)

Bei den Leitern ist es schließlich so, dass das Leitungs­band bis in das Valenz­band hinein­reichen kann. Und damit hat man einen fließenden Austausch von Elektronen.

Grafik/Folie (wird später eingefügt)

Bei metallischen Leitern kann man gar nicht mehr zwischen den bei­den Bändern unter­scheiden. Dort können sich die Elektronen weitest­gehend frei bewegen. Die gravierenden Unter­schiede der Leit­fähigkeit für Metalle einer­seits, und für Nicht­leiter und Isolatoren ander­seits, hängen mit der Größe der Energie­lücke bzw. Band­lücke zwischen dem Valenz­band und dem Leitungs­band zusammen.

Das Valenzband ist das letzte Energie­band, das noch mit Elektronen vollends gefüllt ist. Und erst dann kommt das Leitungsband.

Mit dem Bänder­modell lässt sich auch die sogenannte Kontakt­span­nung erklären. Denn unter­schiedliche Metalle haben verschiedene Energie­niveaus, bis zu denen das Leit­fähigkeits­band mit Elektronen gefüllt ist.

Da gibt es zum Beispiel einige Metalle, deren Energie­niveaus nur bis zu einer relativ niedrigen Energie gefüllt sind. Und andere, bei denen die Energie um einiges höher ausfällt. Wenn Metalle mit derart unter­schiedlichen Energie­niveaus miteinander in Kontakt kommen, hat das entsprechende Auswirkungen. Eine klassische Material­paarung wäre beispiels­weise Kupfer und Zink. Die Energie­grenze der Elektronen in den Valenz­bändern reicht bei diesen beiden Metallen bis zu einer jeweils unter­schied­lichen Höhe. Damit ist der Abstand bis zum Leit­fähigkeits­band bei Kupfer größer als bei Zink. Das bedeutet, wenn aus einem solchen Metall ein Elektron heraus­geschlagen werden soll, dann muss eine Austritts­arbeit über­wunden werden. Und je tiefer das letzte Energie­niveau ist, desto größer wird die Austritts­arbeit sein, die erfor­der­lich ist. Diese Energie­grenze nennt man auch die „Fermigrenze”. Bei zwei verschiedenen Metallen sind diese Grenzen entsprechend unter­schiedlich. Metalle mit der niedrigeren Fermigrenze sind die „edleren Metalle”, so wie zum Beispiel Silber, Gold oder Platin. Bei diesen Metallen benötigt man viel Energie, bis ein Elektron frei­gegeben wird. Während „unedle Metalle”, wie zum Beispiel Zink, weniger Energie benötigen, um ein Elektron herauszuschlagen.

Grafik (wird später eingefügt)

Wenn man also zwei Metalle mit­einander in Kontakt bringt, wie zum Beispiel Kupfer und Zink, werden Elektronen herüber diffun­dieren. Auf der Kupfer­seite wird es zunehmend negativ, weil negative Elektronen vom Zink herüber­wandern. Und auf der Zink­seite wird es zunehmend positiv, so dass sich beide Metalle letzten Endes angleichen. Diese Kontakt­spannung, die man dadurch erhält, lässt sich wie folgt dar­stellen:

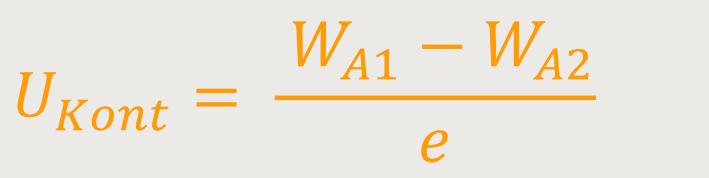
Grafik (wird später eingefügt)

Aufgrund dieser Mechanismen lässt sich eine Kontakt­spannungs­reihe aufstellen:

Von unedlen Metallen (positiv) ... bis zu ... edlen Metallen (negativ):

(positiv)   Rb − K − Na −
... − ...
− Cu − Au − Pt   (negativ)

Diese Eigenschaft, dass die edlen Metalle nur wider­strebend Elektro­nen hergeben, sorgt dafür, dass sie auch chemisch beständiger sind.

⇦ Kapitel Kapitel ⇨