Die „elektrische Leitfähigkeit” ist eine weitere wichtige Größe. Hierzu betrachten wir wieder einen langen, dünnen Leiter, an dessen Enden ein elektrisches Feld angelegt wird. Als Folge davon wird in dem Leiter eine „Driftgeschwindigkeit” der Ladungsträger entstehen. Kennt man diese Geschwindigkeit, erhält man auch die Stromdichte.
Für isotrope Leiter gilt, dass die Stromdichte und die elektrische Feldstärke
zueinander parallel sind
 ||
||

Des Weiteren werden die Stromdichte und die elektrische Feldstärke zueinander proportional sein:
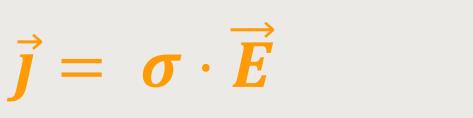
σ ist die elektrische Leitfähigkeit (ein Proportionalitätsfaktor)
Diese Beziehung nennt man auch das (differentielle) Ohm'sche Gesetz.
Je größer die elektrische Leitfähigkeit ist, desto größer wird bei einem bestimmten angelegten Feld die Stromdichte sein.
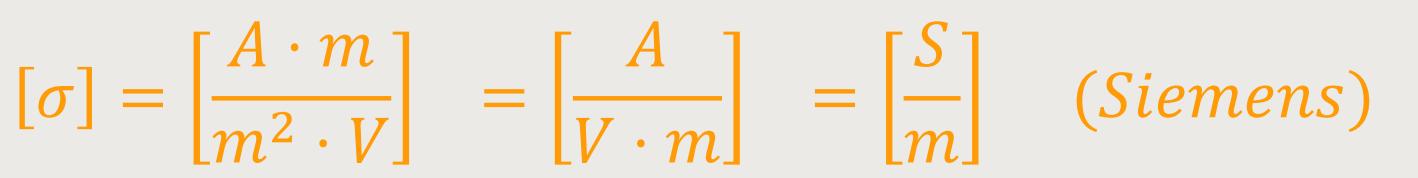
Einige Werte für die elektrische Leitfähigkeit σ [S/m] sind:
| Werkstoff | Leitfähigkeit |
|---|---|
| Ag (Silber) | 62 × 106 |
| Cu (Kupfer) | 59 × 106 |
| Al (Aluminium) | 37 × 106 |
| Fe (Eisen) | 10 × 106 |
| Kohle (Aluminium) | 0,01 × 106 |
| Bernstein | 2 × 10−15 |
| Quarz | 10−18 |
Die elektrischen Ströme, mit denen wir es im Allgemeinen zu tun haben, fließen durch Leiter. In diesem Fall sprechen wir von metallischen Leitern. Man kann davon ausgehen, dass die Stromdichte in einem solchen Leiter proportional ist zu der angelegten elektrischen Feldstärke. Das ist der Fall, weil die Leitungsladungen (Elektronen, Ionen) sich so bewegen werden, wie es dem angelegten Feld entspricht. Denn die Feldstärke beschreibt ja die Kraft auf die Ladungen.
Dieser Zusammenhang lässt sich in dem bereits erwähnten differentiellen Ohm'schen Gesetz (s.o.) darstellen:
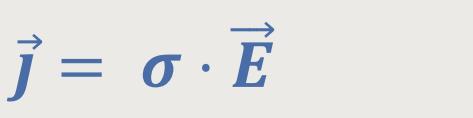
σ ist der Proportionalitätsfaktor (s.o.)
Wir wollen jetzt aber von einer differentiellen Gesetzmäßigkeit auf eine integrale Gesetzmäßigkeit übergehen, weil sich diese für praktische Anwendungsfälle besser eignet.
Für die nachfolgenden Überlegungen betrachten wir wieder einen homogenen zylindrischen Leiter.
Grafik (wird später eingefügt)
A ist der Leiterquerschnitt
L ist die Länge des Leiters
Hierzu wird obige Gleichung mit der Querschnittsfläche A erweitert:
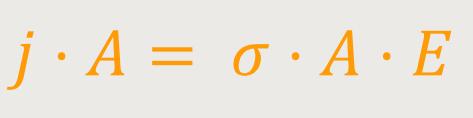
Man kann sofort erkennen, dass
Daraus ergibt sich dann:
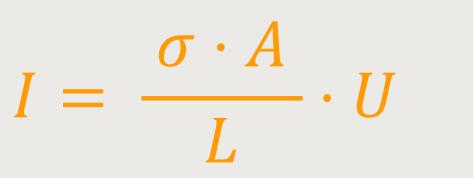
Damit erhalten wir für die Spannung:

R ist der Widerstand
Das ist das „klassische” (integrale) Ohm'sche Gesetz:
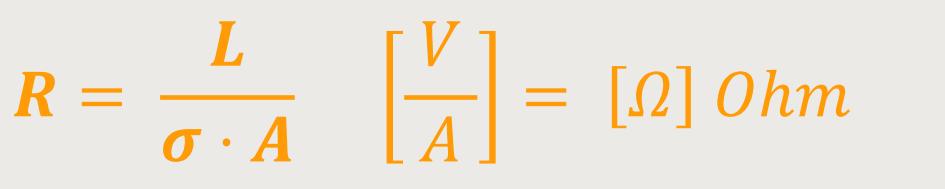
Der „Widerstand” ist demnach ein Verhältnis der Länge zur elektrischen Leitfähigkeit in Abhängigkeit vom Querschnitt. Je größer die Leitfähigkeit, desto kleiner wird der Widerstand. Und je länger der Leiter, desto größer wir sein Widerstand sein.
In der Elektrostatik hatte sich für stromdurchflossene Leiter ergeben, dass es innerhalb des Leiters keine Potentialunterschiede gibt. Ansonsten würde es zu Ladungsverschiebungen in dem Leiter kommen. Und zwar solange, bis es zu einem statischen Gleichgewichtszustand kommt.
Im vorliegenden Fall hat man aber eine andere Situation. Legt man an den Enden des Leiters eine Spannung an, erzwingt man einen Ladungstransport. Aufgrund dessen kommt es zu einem Spannungsabfall längs eines stromdurchflossenen Leiters.
Grafik (wird später eingefügt)
So eine Beziehung bleibt aber nicht über alle Größenordnungen hinweg gültig. Wenn man zum Beispiel einen Widerstand wählt, der sich bei einem sehr hohen Strom erhitzt, dann wird sich auch der Widerstand ändern. Beispielsweise kommt es bei metallischen Leitern aufgrund der erhöhten thermischen Bewegung der Gitteratome zu einer größeren Behinderung der Leitungselektronen. In diesem Fall sind Strom und Spannung nicht mehr proportional zueinander.
Grafik (wird später eingefügt)
Aus diesem Grund unterscheidet man bei den elektrischen Widerständen zwischen zwei Zuständen. Im ersten Fall haben wir eine „lineare” Abhängigkeit zwischen der Spannung und der Stromstärke:

Im zweiten Fall haben wir eine „differentielle” Abhängigkeit zwischen der Spannung und der Stromstärke:
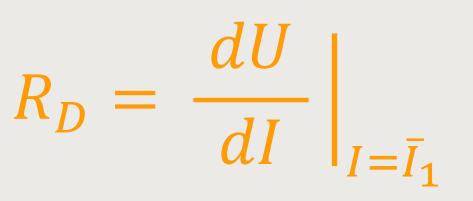
Hierbei ist von Interesse, wie sich das System auf die unmittelbare Umgebung des jeweils gewählten Arbeitspunktes auswirkt.
⇦ Kapitel Kapitel ⇨
