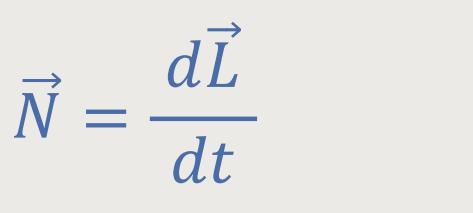Sprechen wir noch kurz über die Dynamik der Kreisel­bewegung. Um diese Dynamik richtig darstellen zu können, benötigt man eine Differenzial­gleichung, quasi eine Bewegungs­gleichung. Das ist wie schon oft erwähnt:

Damit man ein anschau­liches Ergebnis erhält, muss man auch hier auf das körper­feste Koordinaten­system trans­formieren. Auch hier­für wählt man wieder das Haupt­achsen­system, als besonders bevor­zugtes körper­festes Koordinaten­system.

Daraus erhält man die berühmten Eulerschen Kreisel­gleichungen. Diese werden meistens in Kompo­nenten­form aufge­schrieben. Eine für die A-, eine für die B-, und eine für die C-Komponente. Das sind drei Differential­gleichungen, die mitein­ander gekoppelt sind. Hier beschränken wir uns jedoch nur auf symme­trische Kreisel. Wenn zwei von drei Haupt­trägheits­momenten gleich sind, spricht man von einem symme­trischen Kreisel.

Es gibt jetzt drei wichtige Achsen bzw. Achsen­richtungen. Die erste Achse ist natürlich die raum­feste Dreh­impuls­achse . Wenn kein äußeres Dreh­moment wirkt, dann ist konstant. Als zweites gibt es die Dreh­achse, die durch den Winkel­geschwindig­keits­vektor 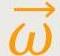charakte­risiert ist. Und weil dieser Kreisel symme­trisch ist, gibt es als drittes die Figuren­achse. Letzt­genannte ist eine Achse, welche durch die Symmetrie­linie dieses symme­trischen Kreisels verläuft.

Wenn alle Achsen parallel zueinander verlaufen, erhält man eine stabile Rotation. Dann liegt ein spezieller Fall vor:

Je nach Anfangs­bedingungen muss das nicht zwingend so zu sein. Erfolgt zum Beispiel ein kurz­zeitiger Impuls von außen, dann taumelt die Figuren­achse des Körpers um die raum­feste Dreh­impuls­achse herum. Durch Lösung der Eulerschen Kreisel­gleichungen lässt sich beweisen, dass zwei Winkel immer gleich sind. Das ist zum einen der Winkel zwischen Figuren­achse und Dreh­impuls­achse. Und ander­seits der Winkel zwischen Figuren­achse und Rotations­achse. Beide Winkel bleiben immer konstant.

Diesen Vorgang, nämlich der Rotation ohne äußeres Dreh­moment und bei dem alle drei Achsen nicht parallel zueinander verlaufen, nennt man die „Nutation des Kreisels”. Nutation ist eine Rotations­bewegung, wo diese drei Achsen nicht zusammen­fallen. Dieser Fall ist der Gegen­satz zur stabilen Rotation. Und wenn diese zwei Winkel immer konstant bleiben, dann bedeutet das:
Der Gangpol­kegel rollt an dem raumfesten Rastpol­kegel tangential ab, wobei der Gangpol­kegel in dem starren Körper verankert ist. Das Ganze nennt man dann die „Nutationsbewegung”. Den Rastpol­kegel nennt man so, weil er in Ruhe ist, relativ zum raum­festen Dreh­impuls. Also relativ zu dem raum­festen Inertial­system, zu dem sich dieser Kreisel dreht.

Hinweis: Die Figurenachse ist zugleich die Symmetrieachse des starren Körpers.

Was passiert, wenn ein „äußeres Dreh­moment” wirkt? Ein äußeres Moment kann dadurch zustande kommen, wenn ein solcher Kreisel schräg auf einer Auflage­fläche aufsitzt, und der Körper aufgrund der Schwer­kraft umkippt, sobald er sich nicht mehr dreht.

Wir werden jetzt eine Situation betrachten, wo keine Nutation vorhanden ist, wo also eine stabile Rotation vorliegt, und wo der Dreh­impuls­vektor, die Figuren­achse und die momen­tane Dreh­achse zusammen­fallen. Bei dieser Betrach­tung sieht man, dass der Körper eine anders­artige Bewegung durch­führt als bisher. Jetzt bewegt sich der ganze Dreh­impuls­vektor mit herum. Insofern kippt der Körper nicht mehr nach unten, sondern weicht bedingt durch die Rotation seitlich aus.

Die Figuren­achse, die zugleich der Dreh­impuls­achse und zugleich der momen­tanen Dreh­achse entspricht, bewegt sich ihrer­seits auf einem Kegel­mantel. Das ist jetzt eine völlig andere Situation als zuvor. Man nennt das auch eine „Präzession”. Diese Bewegung entsteht erst durch die Einwirkung des äußeren Dreh­moments, hervor­gerufen durch die Schwer­kraft, und führt zu einer derartigen Bewegung.

Auch hier spielt die Bewegungsgleichung wieder einer Rolle:

Das bedeutet aber, wenn man Verände­rungen in kurzen Zeit­inter­vallen Δt betrachtet, und wie folgt schreiben kann:

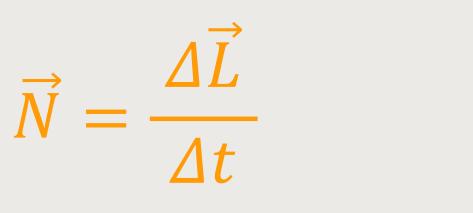
Ein Differenzial­quotient ist ja nichts anderes als der Limes von solchen Differenzen, wenn diese Differenzen des Argumentes gegen Null gehen. Nach Umformen erhält man:

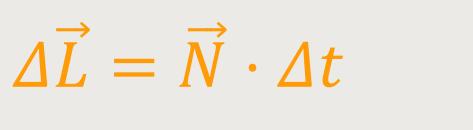
Das heißt, man kann aufgrund dieser Bewegungs­gleichung damit rechnen, falls ein äußeres Dreh­moment auf den rotierenden starren Körper wirkt, dass sich dann der Dreh­impuls­vektor um einen kleinen Vektor Δ ändern wird, in einer kurzen Zeit Δt. Diese Ände­rung ist parallel zum Dreh­moment­vektor .

Wenn man jetzt bei diesem Kreisel die Eigen­rotations­winkel­geschwindigkeit ändert, was passiert dann mit der Winkel­geschwindig­keit der Präzessions­bewegung?

Sobald man die Eigen­rotations­winkel­geschwindigkeit verringert, erhöht sich die Winkel­geschwindig­keit der Präzessions­bewegung. Wie kann man das verstehen?

Bei einer stabilen Rotation ist der Dreh­impuls­vektor definiert als:

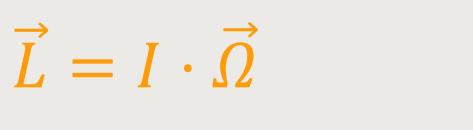
I    ist das Trägheits­moment um die Haupt­achse (Figuren­achse)
  ist die Winkel­geschwindig­keit

Das heißt, wenn jetzt die Winkel­geschwindig­keit kleiner wird und sich der Kreisel langsamer um seine Achse dreht, dann wird auch der Vektor kürzer. Der Dreh­impuls wird somit kleiner, weil auch die Winkel­geschwindig­keit kleiner wird. Die Länge des Dreh­impuls­vektors Δ ist davon nicht betroffen, er bleibt gleich groß. Denn der Dreh­impuls hängt von der Winkel­geschwindig­keit gar nicht ab. Das heißt, es muss in der Zeit Δt ein größerer Winkel zurück­gelegt werden. Der Grund dafür ist, weil sich ein kürzerer Dreh­impuls­vektor um den gleichen Differenz­vektor verändert.

In diesem Zusammen­hang sei erwähnt, dass beide Effekte − Nutation und Präzession − natürlich auch gemeinsam auftreten können.

Die Präzes­sion hat auch eine wichtige Auswirkung auf die Bewegung unserer Erde. Es zeigt sich nämlich, dass die Erde aufgrund ihrer Eigen­rotations­bewegung leicht abge­plattet ist aufgrund der Zentrifugal­kräfte, die auf die Erde wirken. Man kann davon ausgehen, dass es bei unserer Erde eine „einge­schriebene” Kugel gibt. Seit­lich gibt es zusätz­liche sichel­förmige Massen, um die sich der reale Erd­körper von einer Kugel unter­scheidet. Diese zwei sichel­förmigen Massen haben zwei Schwer­punkte, S₂ und S₂.

Aufgrund der unter­schied­lichen Abstände der Schwer­punkte zur Sonne gibt es in Richtung des Zentral­gestirns Differenz­kräfte. Es gibt ein Kräfte­paar, welches auf die beiden Schwer­punkte wirkt und entgegen­gesetzt gedacht sein muss. Und dieses Kräfte­paar bewirkt ein Dreh­moment auf die Dreh­achse, die ihrer­seits quer dazu abweichen wird. Und das bedeutet wiederum, dass diese Achse eine Präzes­sions­bewegung um die senk­rechte Achse durch­führen wird. Da die Effekte nicht sehr groß sind passiert das nicht sehr rasch. Es zeigt sich aufgrund von Beobach­tungen, dass ca. 26.000 Jahre verstreichen müssen, bis die Präzes­sion einmal rund herum geht.

⇦ Kapitel Kapitel ⇨