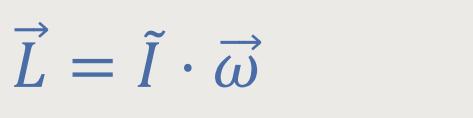Jetzt wollen wir die Einschrän­kung der Rotation um eine bestimmte Achse aufheben. Der starre Körper kann sich nun in allen Richtungen frei bewegen. An dieser Stelle sei bereits erwähnt, dass wir die Eulerschen Kreisel­gleichungen nicht im Detail betrachten werden.

Dennoch wollen wir kurz unter­suchen, wie sich bei einer beliebigen Rotation eines starren Körpers die Zusammen­hänge dar­stellen. Jetzt geht es nicht mehr um eine feste Dreh­achse, sondern um eine Rotation um seinen Schwer­punkt. Dieser Schwer­punkt muss ein raum­fester Punkt sein, ruhend in Bezug auf das Inertial­system. Ansonsten gibt es keine weiteren Einschrän­kungen. Die Dreh­achse muss jedoch immer durch den Schwer­punkt durchgehen. Auch hier geht es um den Zusammen­hang zwischen:

Hinweis: Wie wir bereits behandelt haben, ist diese Schreib­weise die Kurzform der Matrizen­schreib­weise.

Vorweg kommt noch eine sehr wichtige Über­legung. Wenn man sich die Kompo­nenten des Trägheits­tensors anschaut, dann sind das ja Integrale über den ganzen starren Körper. Also über seine Volumen- bzw. Massen­elemente. Nun ist es aber so, dass dieser starre Körper rotiert und zwar völlig frei im Raum. Nur sein Schwer­punkt bleibt fest.

Naheliegend wäre es jetzt, sich bei der Berechnung des Trägheits­tensors auf das raum­feste Koordinaten­system zu beziehen. Der ist ja verankert im Inertial­system, und dreht sich relativ zum betrach­teten Körper. Dann würden alle seine Kompo­nenten I_{i j} zeitab­hängig werden. Wenn sich dieser Körper dreht und man würde ein Integral über das Volumen bilden, dann läge das Volumen immer wieder woanders. Das heißt, man erhielte einen zeitab­hängigen Trägheits­tensor. Diese Vorgehens­weise ist äußert unpraktisch.

Zwar hat man mit dem raum­festen Koordinaten­system den Vorteil, dass bei fehlendem äußeren Dreh­moment der Dreh­impuls­vektor raumfest bleibt. Aber das kann man nicht immer voraus­setzen. Deshalb geht man jetzt so vor, dass man von dem raum­festen auf ein körper­festes Koordinaten­system über­geht. Hierzu macht man eine Trans­formation zu einem körper­festen Koordinaten­system. Welchen Vorteil hat das?

Wenn ein Koordinaten­kreuz mit dem Körper verankert ist, und man sich die Durch­führung der Integrale über die Volumen­elemente des Körpers bzw. die Massen­elemente betrachtet, dann ruhen sie nun relativ zum Körper. Damit erreicht man jetzt, dass alle 9 Komponenten (I_{₁ ₁} ... I_{₃ ₃}) zeitunab­hängig werden. Und letzt­lich sind für die Eigen­heiten dieses speziellen Körpers nur mehr diese 9 Kompo­nenten charakte­ristisch.

Hinweis: Der Vektor der Winkel­geschwindig­keit, also das 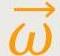, soll nach wie vor, auch wenn man eine solche Trans­formation durch­führt, die Rotation dieses starren Körpers relativ zum raum­festen System darstellen. Und der Dreh­impuls­vektor soll genauso den Dreh­impuls aus der Sicht des raum­festen Koordinaten­systems dar­stellen.

Also der Körper rotiert wie gewohnt, relativ zum Inertial­system. Und dieses rotierende System, an welches dieses körper­feste Koordinaten­system angehängt ist, ist auch kein Inertial­system im Allge­meinen. Es ist nur eine Darstellung aller dieser Vektoren mit Hilfe eines anderen Koordinaten­kreuzes. Die Vektoren als solche und auch der Tensor als solcher bleiben was sie sind.

Der Hauptzweck, warum man so vorgeht ist, damit in dieser Beziehung alle I_{i j} während der Rotation konstant bleiben. Nach­teilig ist aller­dings, dass aus Sicht des Koordinaten­systems auch ein raum­fester Dreh­impuls mit herum taumelt. Aber dieser Nach­teil fällt insgesamt weniger ins Gewicht.

Hier erkennt man schon, wie wichtig das Konzept der Tensor­rechnung ist. Man kann auf unter­schiedliche Bezugs­systeme wechseln. Tensoren (zweiter Stufe) sind einfach Matrizen, mit dem richtigen Trans­formations­verhalten. Das heißt, die Kompo­nenten I_{i j} werden sich korrekt verändern, wenn man trans­formiert. Und weil sich auch die Komponenten von und 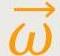trans­formieren, wird letzt­lich der Zusammen­hang erhalten bleiben.

Jetzt lässt sich das aber noch weiter optimieren. Man hat zwar mit einem körper­festen Koordinaten­system schon viel gewonnen. Aber für reelle symme­trische Matrizen gibt es zusätz­lich noch die Möglich­keit einer Haupt­achsen­trans­formation. Hierzu wählt man ein optimal gelegenes ortho­gonales Koordinaten­kreuz inner­halb des betrach­teten starren Körpers. Nach einer solchen Trans­formation ist das Hauptachsen­system schließlich so beschaffen, dass von dem Trägheits­tensor nur mehr die Diagonal­elemente übrig bleiben und alles andere Null wird.

Diese Vorgehens­weise kennen wir bereits aus der Rotation um eine feste Dreh­achse. Im Allge­meinen hat man es ja mit symme­trischen Körpern zu tun. Und wenn ein Körper bezüg­lich einer bestimmten Achse symme­trisch ist, dann wird das mit Sicher­heit eine der Haupt­trägheits­achsen sein.

Daraus folgt, dass der Trägheits­tensor nur noch drei Kompo­nenten hat:

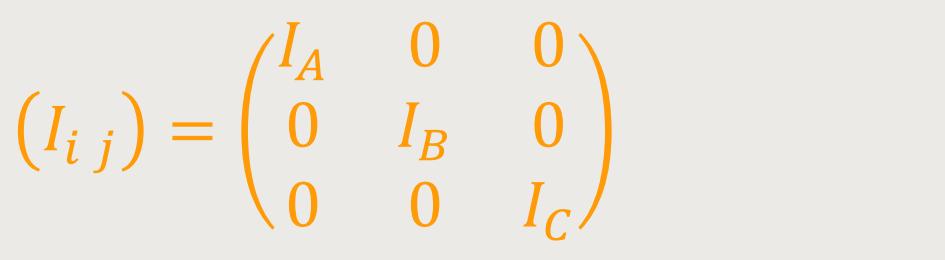
Und falls ein Körper nicht symme­trisch ist, gibt es trotz­dem eine solche Haupt­achsen­trans­formation. Außer­dem kann man durch Wahl der Achsen, nämlich welches die erste, die zweite und die dritte ist bestimmen, dass diese wie folgt angeordnet sind:

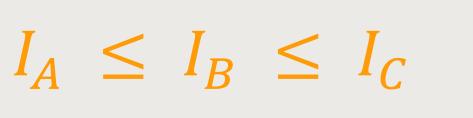
Das sind dann die Haupt­trägheits­momente eines beliebig geformten starren Körpers.

Wenn alle drei Trägheits­momente unter­schiedlich sind, handelt es sich in jedem Fall um einen „unsymme­trischen Körper”. Wenn zwei gleich sind, dann ist das ein „symmetrischer Kreisel”. Und wenn alle drei gleich sind, dann nennt man den Körper einen „Kugel­kreisel”. Ein würfelförmiger Körper ist auch Kugel­kreisel. Letzt­lich richtet sich alles nur danach, welche Form der Körper hat.

Insofern ist der Trägheits­tensor charakte­ristisch für die entspre­chende Form und die Massen­verteilung inner­halb eines Körpers. Was können wir jetzt damit anfangen? Zunächst sei erwähnt, nur im Haupt­achsen­system werden die Haupt­achsen mit A, B und C bezeichnet. Für die Kompo­nenten des Winkel­geschwindig­keits­vektors gilt somit:

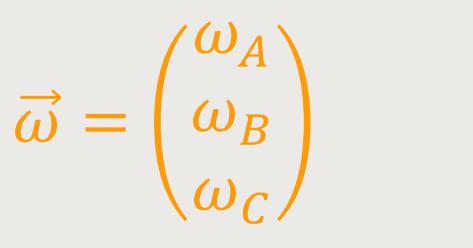
Und für den Drehimpuls­vektor gilt:

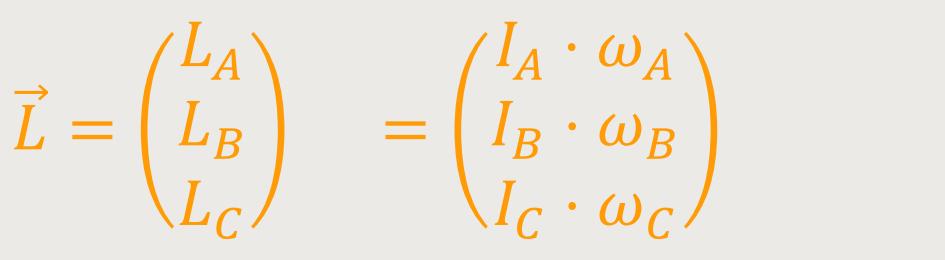
Aus diesem Zusammen­hang kann man bereits erkennen:

Damit liegt auf der Hand, dass man spezielle Dreh­achsen verwenden kann. In diesem Fall wählt man die Rotation um eine der Haupt­trägheits­achsen.

Die Haupt­trägheits­achsen sind körper­feste Achsen. Zum Beispiel kann ein Zylinder um die erste Haupt­achse rotieren. „Ohne Beschränkung der Allge­meinheit wählen wir die Erste” (Redewendung aus der Mathematik):

Weil die Dreh­achse parallel zur A-Achse des körper­festen Haupt­achsen­systems ist, hat der Körper keine B- und C-Komponenten. Damit erhält man für den Dreh­impuls­vektor:

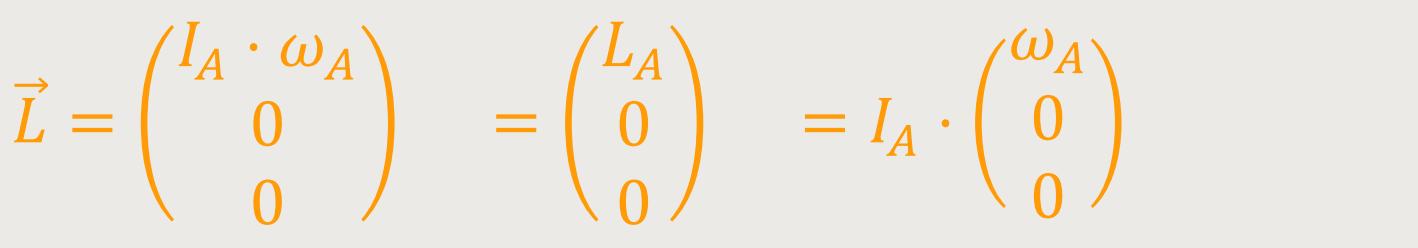
Das heißt, es gibt nur einen Dreh­impuls­vektor.

Wenn man den Trägheits­tensor multi­pliziert mit dem Vektor der Winkel­geschwindig­keit kommt ein Viel­faches der Winkel­geschwindig­keit heraus:

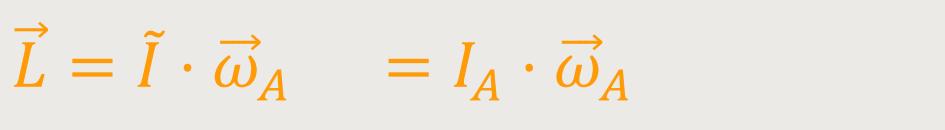
So etwas nennt man auch eine „Eigen­wert­gleichung”. Wenn man einen Operator auf einen Vektor anwendet, kommt das Viel­fache dieses Vektors heraus. In diesem speziellen Fall ist:

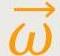Wenn man also den Zylinder um seine Haupt­achse drehen lässt, dann wird der zuge­hörige Dreh­impuls­vektor auch in diese Richtung zeigen. Oder anders ausge­drückt, der Dreh­impuls­vektor verläuft in diesem Fall parallel zum Winkel­geschwindig­keits­vektor _A.

Nun kommt noch ein weiterer Aspekt hinzu. Wir können jetzt auch die kinetische Energie für die Rotation dieses Körpers ausrechnen. Sie ist Allge­mein definiert als:

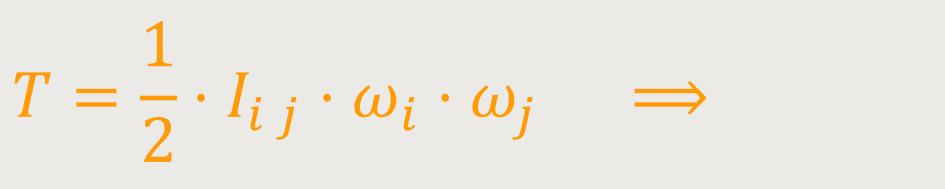
Wie wir im vorherigen Kapitel gesehen haben, ist dies eine Doppel­summe. Aber in unserem speziellen Fall, nämlich im Haupt­achsen­system, kommt heraus:

Das ist alles, was aus der Doppel­summe übrig bleibt. Es lässt sich durch Umformen auch wie folgt darstellen:

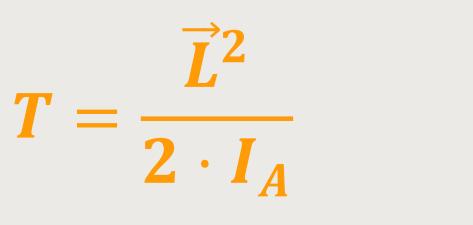
Damit erhält man eine wichtige Folgerung. Wenn man ein System mit konstantem Dreh­impuls betrachtet, also wenn kein äußeres Dreh­moment vorhanden ist, dann wird das ^₂ eine Konstante sein.

Und wann wird in diesem speziellen Fall die kinetische Energie T am kleinsten sein? Um welche Haupt­achse muss sich der Körper dann drehen? In unserem Beispiel wäre das die Achse I_C. Das wird für das System die stabilste Rotation sein, weil die energe­tisch niedrigste Situation immer die günstigste ist. Die stabilste Rotation ist die mit der kleinsten Energie. Das heißt, dass die stabilste Rotation die um die Achse des größten Trägheits­moments verläuft.

Versuche mit verschie­denen Körpern zeigen, dass ein Körper der sich selbst über­lassen ist, am liebsten stabil um die Achse des größten Trägheits­moments rotiert, weil eine solche Rotation mit der kleinsten kinetischen Energie einhergeht.

⇦ Kapitel Kapitel ⇨