Im vorherigen Kapitel haben wir den Zusammen­hang zwischen dem Dreh­impuls­vektor und dem Winkel­geschwindig­keits­vektor erarbeitet.

Wie kann man jetzt diesen einfachen Forma­lismus in ein anschau­liches Beispiel über­tragen? Im Wesent­lichen ging es ja um folgende beiden Formeln:

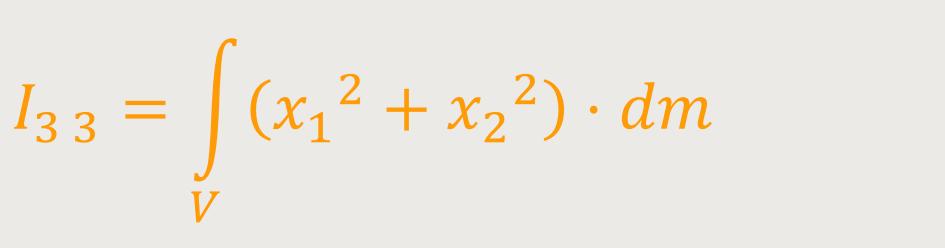
Interessant wird es dann, wenn man die gesamte kinetische Energie dieses rotie­renden starren Körpers ausrechnen möchte. Wir behalten dabei im Sinn, dass man es mit einem ausge­dehnten Körper zu tun hat, der aus einzelnen Massen­elementen bzw. Volumen­elementen besteht. Dieser Körper rotiert mit einer Winkel­geschwindig­keit um eine Dreh­achse.

Und wenn man jetzt die gesamte kinetische Energie dieser Drehung ermitteln möchte, müsste man eigent­lich alle diese einzelnen Massen­elemente, aus denen der Körper besteht, hernehmen, und deren jeweilige kinetische Energie ausrechnen. Und dann wie gewohnt aufsummieren oder aufinte­grieren. Der Einfachheit halber wird man das als Integral schreiben.

Ziel der Integration ist es ja, die Einteilung in einzelne Volumen- oder Massen­elemente immer feiner und feiner zu wählen. Und letzt­lich kann man im Limes, also im Grenz­wert, eine präzise Aussage gewinnen. In der Praxis ist es dann oft so, dass man nur eine genügend feine Einteilung wählt und dann darüber summiert. Das reicht in der Regel oftmals schon aus.

Die gesamte kinetische Energie stellt sich dann dar als:

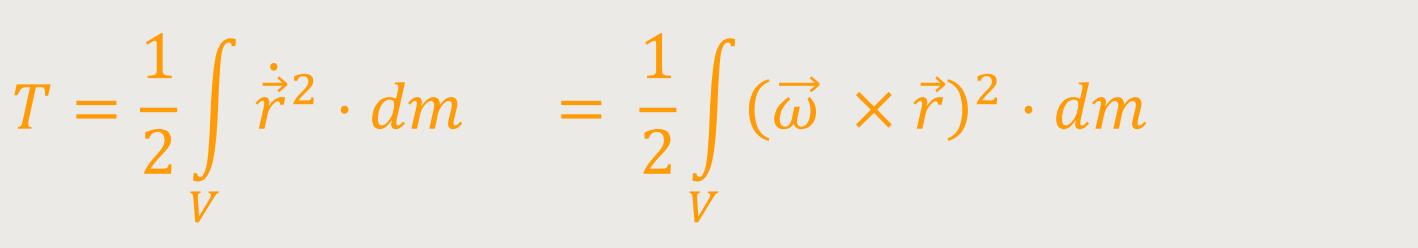
dm ist ein einzelnes Massenelement
ist die Geschwindigkeit dieses Massenelementes

Auf Grundlage verschie­dener Formeln aus der Vektor­rechnung und der Komponenten­schreib­weise ergibt sich nach einigen Umformungen:

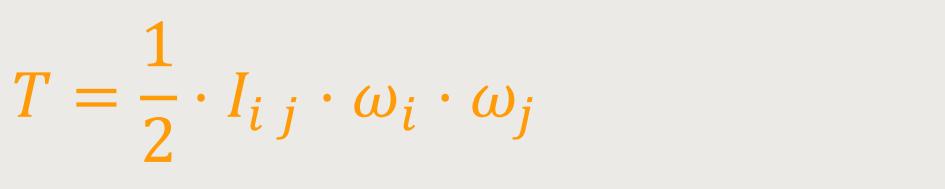
In dieser Beziehung verstecken sich 9 Terme, die wir hier nicht noch­mals dar­stellen werden. Aus den Indizes erkennt man außerdem, dass hier eine Doppel­summe gebildet wird. Die Vorgehens­weise haben wir bereits im vorherigen Kapitel erläutert.

Für eine Rotation um eine vorhandene Dreh­achse tragen alle einzelnen Elemente des Trägheits­tensors zur kinetischen Energie bei. Wie kann man jetzt mit Hilfe dieser allge­meinen Bezie­hungen relativ schnell auf ein konkretes Ergebnis kommen?

Hierzu wollen wir einen ein­fachen Spezial­fall betrachten. Es geht zunächst um die Rotation um eine feste im Raum vorgegebene Achse. Eine beliebige Rotation um irgend­eine Achse betrachten wir später.

Natürlich kommt es auch wieder darauf an, dass man bei der Wahl des Koordinaten­systems die Achse mit berück­sichtigt. Wir gehen also davon aus, dass die Rotations­achse auf der x_₃-Achse des Koordinaten­systems liegt. Wenn man das so wählt, dann liegt der Winkel­geschwindig­keits­vektor parallel zur Dreh­achse.

Ist die Dreh­achse auf diese Weise fest gewählt, dann ergibt sich für die Komponenten des Vektors:

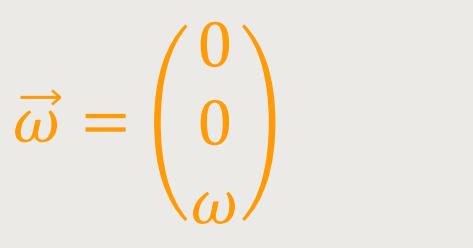
Das macht die Sache natürlich wesent­lich einfacher.

Da wir nur eine Rotation um die x_₃-Achse betrachten, interessiert uns in erster Linie auch nur die dritte Komponente des Dreh­impuls­vektors. Daraus ergibt sich dann für den Dreh­impuls:

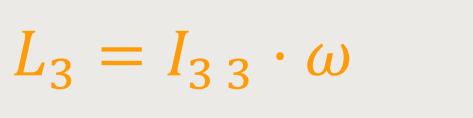
Somit reduziert sich obige Tensor-Beziehung auf eine einfache Beziehung zwischen der dritten Komponente des Dreh­impuls­vektors und der Winkel­geschwindig­keit . Im Grunde ist dieses L_₃ nichts anderes als die Parallel­komponente des Dreh­impulses parallel zur Drehachse.

Es wäre auch eine andere Schreib­weise in Form eines Vektors möglich:

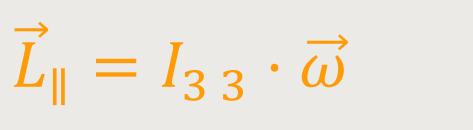
Für eine derartige Rotation, bei der es in erster Linie um die Parallel­komponente des Dreh­impuls­vektors geht, kommt es im Wesent­lichen auf die Komponente I_{₃ ₃} des Trägheits­tensors an. Diese Komponente wird uns im weiteren Verlauf besonders interes­sieren. Man kann aber auch entspre­chend obiger Beziehung die kinetische Energie wie folgt darstellen:

Von der ganzen Doppel­summe mit den 9 Termen bleibt also nur mehr 1 Term übrig. Wenn es wie in unserem Fall um eine Rotation um eine feste Dreh­achse geht, kommt es nur auf das I_{₃ ₃} an. Damit haben wir eine völlig analoge Beziehung, wie wir sie bereits aus der Dynamik der Trans­lations­bewegung kennen.

Um das im weiteren Verlauf auch real ausrechnen zu können ist es nützlich, sich etwas mit der Geometrie zu beschäftigen.

Die Berechnung der Komponente I_{₃ ₃} des Trägheits­tensors lautet:

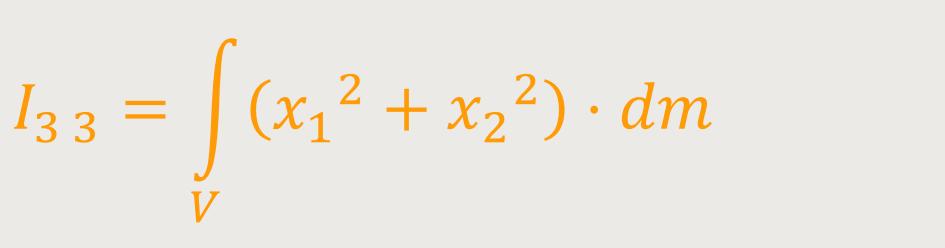
Es geht darum sich klarzu­machen, was dieser Integrand (x_₁^₂ + x_₂^₂) ist.

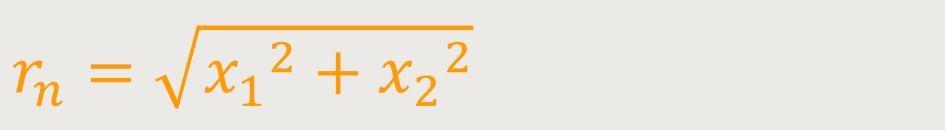
In diesem Fall ist r_n der Normal­abstand des betreffenden Massen­elements dm von der Dreh­achse aus. Wenn man über alle diese Massen­elemente dieses starren Körpers aufsummiert bzw. integriert, dann kommt man auf das I_{₃ ₃}.

I_{₃ ₃}   ist das Trägheits­moment des starren Körpers (bezüglich der festen Achse)

Man braucht nur die Summe oder das Integral r_n² · dm bilden. Hierzu nimmt man alle Massen­elemente her, aus denen dieser Körper besteht. Wichtig ist dabei die quadra­tische Funktion. Denn wenn das Massen­element weiter weg ist von der Drehachse, dann trägt es auch mehr zum Trägheits­moment I_{₃ ₃} bei. Oder umgekehrt, je näher das Massen­element an der Dreh­achse liegt, desto weniger wird es zum Trägheits­moment beitragen.

Man könnte sich zum Beispiel gedank­lich einen Körper vorstellen, der eine gewisse Massen­verteilung hat und dem dann ein solches I_{₃ ₃} entspricht. Wenn man den Körper jetzt so verändert, dass dieselben Massen sich etwas anders aufteilen, indem man sie näher an die Dreh­achse heranrückt, dann wird das Trägheits­moment kleiner werden.

Jetzt ist es aber so, dass die Rotation des Körpers ohne Wirkung äußerer Kräfte erfolgt. Dann wird der Dreh­impuls und daher auch seine L_₃-Komponente zeitunab­hängig sein. Wenn dement­sprechend das Trägheits­moment kleiner wird, dann wird bei gleich­bleibendem Dreh­impuls die Winkel­geschwindig­keit größer werden. Das kann man besonders gut bei Eiskunst­läufern beobachten, die eine Pirouette drehen. Damit erhält der Körper auch eine höhere kinetische Energie.

Wenn bei gleich­bleibender Gesamt­masse des Körpers der Abstand, sprich das Trägheits­moment geändert wird, ergibt sich eine andere Situation. Wird das Trägheits­moment verkleinert, indem die r_n² bei gleicher Masse kleiner werden, also bei anderer Anordnung der Masse inner­halb des Körpers, dann wird für den Fall eines konstanten Dreh­impulses L_₃, sich die Winkel­geschwindig­keit ω vergrößern. Wenn das ω doppelt so groß wird, und das I_{₃ ₃} halb so groß, dann wird das ω² viermal so groß und damit die kinetische Energie immer noch doppelt so groß. Wo kommt die Erhöhung dieser kinetischen Energie her?

Wenn man also verschiedene Körper betrachtet, wie kann man deren Trägheits­momente I_{₃ ₃} tatsäch­lich ausrechnen? Man muss einfach nur eine entspre­chende Integration durch­führen.

Betrachten wir nun die Trägheits­momente symme­trischer Körper, zum Beispiel die Rotation eines Zylinders. Zunächst schauen wir uns einen dünn­wandigen Hohl­zylinder an.

Die ganze Masse M ist nur im äußeren Ring vereinigt. Der Abstand von der Drehachse sei R. Alle Massen­elemente haben in diesem Fall den Abstand R.

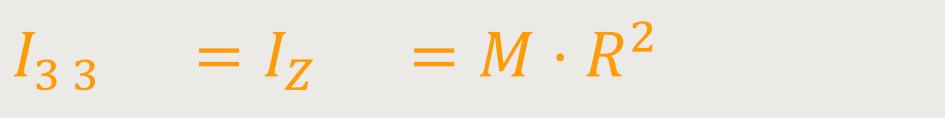
Bei einem Voll­zylinder ist es nicht ganz so einfach. Da muss der Körper zunächst in einzelne Ring­schichten zerlegt werden. Jede dieser Schichten hat dann einen Radius r. Und wenn man anschlie­ßend aufintegriert, erhält man:

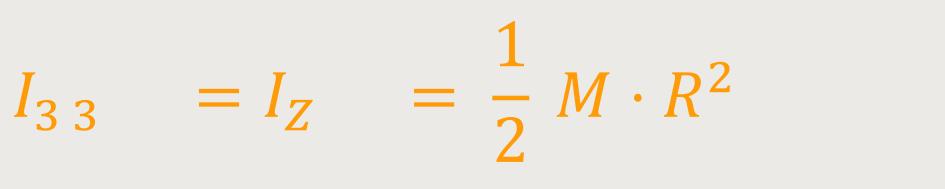
Das Trägheits­moment ist in diesem Fall kleiner, weil sich nicht die ganze Masse im Radius R befindet, sondern sich gleich­mäßig über die ganzen Abstände (Schichten) aufteilt. Und wenn man das aufinte­griert, ergibt sich ein Faktor 1/2.

Oder bei einer homogenen Kugel, die um eine Achse rotiert, die durch den Mittel­punkt der Kugel geht, ergibt sich:

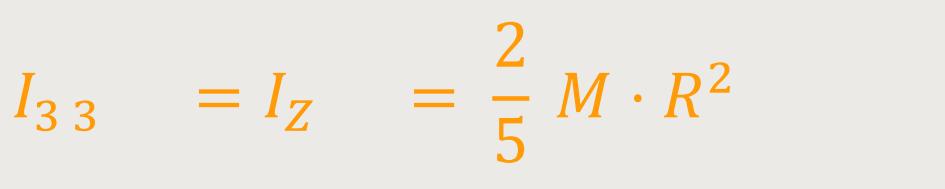
M   ist die gesamte Masse
R   ist der Radius der homogenen Kugel

Die obigen Rechen­faktoren fallen deshalb unter­schiedlich aus, weil die Massen­verteilung innerhalb der Körper unter­schiedlich ist. Das Trägheits­moment hängt nämlich nicht nur von der gesamten Masse des Körpers ab, sondern einer­seits von seiner Form und ander­seits von der Verteilung seiner Massen über sein ganzes Volumen. Das ist hier um einiges komplexer, als bei den trans­latorischen Bewegungen.

Entscheidend ist hierbei, dass sich die Berech­nungen auf symme­trische Körper beziehen, die um eine Symmetrie­achse rotieren. Wie wird sich aber das Trägheits­moment verhalten, wenn man nicht die Symmetrie­achse als Dreh­achse wählt? Vielleicht eine Achse, die nicht durch den Schwer­punkt des Körpers verläuft?

Ein gewisser Jakob Steiner hat einen Satz aufge­stellt. Dieser Satz bezieht sich darauf, wie man das Trägheits­moment bezüg­lich einer parallelen anders gelegenen Nicht­schwer­punkt­achse ausrechnen kann. Hierzu muss man lediglich das Trägheits­moment eines Körpers bezüglich seiner Achse durch den Schwer­punkt kennen. Bei näherer Betrachtung zeigt sich, dass der Zusammen­hang genial einfach ist.

Nehmen wir zum Beispiel einen nicht­symme­trischen Körper. Zunächst wird die Dreh­achse im Schwer­punkt bestimmt. Anschlie­ßend wird eine weitere Achse im Normal­abstand A parallel dazu fest­gelegt, um die der Körper später rotieren soll. Je weiter diese Achse von der Schwer­punkt­achse entfernt ist, desto größer wird dann zwangs­läufig das Trägheits­moment sein.

Wenn man eine Koordinaten-Trans­formation durchführt, erhält man dadurch:

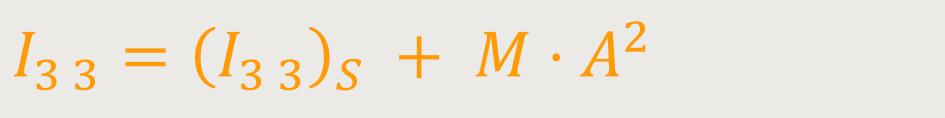
Das ist der berühmte Satz von Steiner.

( I_{₃ ₃} )_S   ist das Trägheitsmoment des Körpers in der Schwerpunktachse
M   ist die gesamte Masse dieses Körpers
A   ist der Normalabstand der Drehachse zur Schwerpunktsachse

Bis jetzt haben wir nur über die Kinematik gesprochen, nämlich wie der Dreh­impuls mit der Winkel­geschwindig­keit zusammen hängt. Jetzt wäre es natürlich auch interessant, die konkrete Dynamik der Rotation um eine feste Achse zu betrachten. Was passiert zum Beispiel, wenn äußere Einflüsse wirksam sind?

Im Fall der Trans­lation haben wir davon gesprochen, dass wenn eine Kraft auf einen Körper wirkt, dieser beschleunigt wird. Jetzt geht es darum, wenn ein äußeres Dreh­moment auf einem Körper wirkt, dass dann eine Winkel­beschleuni­gung auftreten wird. Diese Zusammen­hänge wollen wir in entspre­chender Weise betrachten.

Wir erinnern uns: ist das äußere Dreh­moment und ist der Dreh­impuls. Die grund­legende Gleichung für die Bewegungs­gleichung lautet:

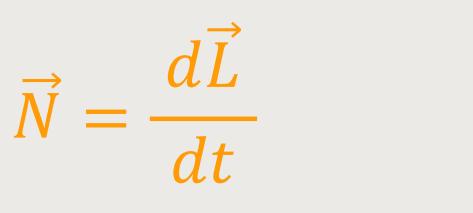
Das ist das Gegen­stück zum 2. Newton-Axiom für die Dreh­bewegung.

Und wieder ist es so, wenn es nur eine Rotation um eine feste Achse gibt, wird auch nur die Parallel­komponente _|| des Drehmoments parallel zu dieser Achse wirksam.

Das ist der Fall, weil die Achs­lager dafür sorgen, dass eine andere Rotation als um die x_₃-Achse gar nicht auftreten kann. Wenn ein anders Dreh­moment vorhanden wäre, würden die Kräfte, die zu einer Rotation um eine andere Achse führen, durch die Zwangs­kräfte in den Lagerungen kompensiert. Die x_₃-Komponente stellt sich dann wie folgt dar:

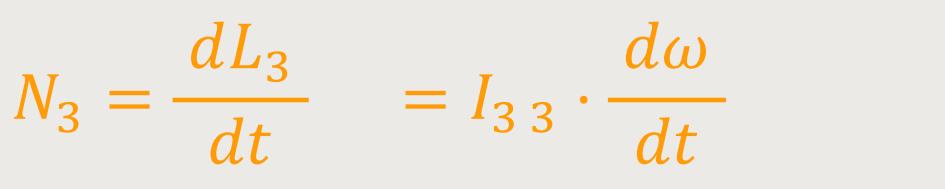
Das ist jetzt das Rotations­gegen­stück zu der Beziehung:
Kraft = Masse · Beschleunigung

Jetzt erhalten wir entsprechend:
Drehmoment = Trägheitsmoment · Winkelbeschleunigung
(N_₃ = I_{₃ ₃} · ω)

Abschließend betrachten wir noch einen sehr einfachen Fall.

Das läuft jetzt nach genau den gleichen Grund­sätzen ab, wie bei der Translation.

Wegen der „gleich­förmigen Beschleuni­gung” nehmen wir ein konstantes Dreh­moment _₀ an. Der Vektor ist zeitunab­hängig und parallel zur Drehachse:

Somit können wir die Bewegungs­gleichung für die x_₃-Komponente aufschreiben:

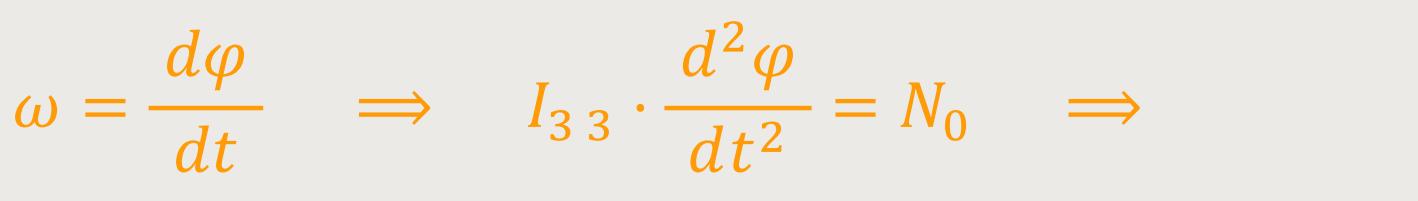
Und damit ist die ganze tensorielle Vorgehens­weise herunter­gebrochen auf eine ganz einfache Differenzial­gleichung, die sich durch zwei Integra­tionen lösen lassen.

Wenn man einmal integriert, erhält man:

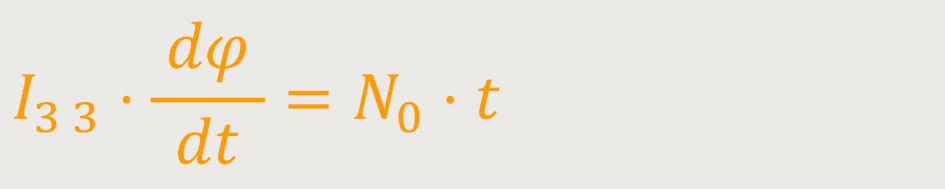
Oder anders ausgedrückt:

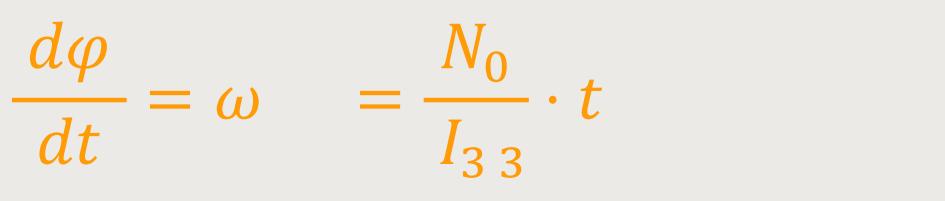
Man sieht sofort, dass die Winkel­geschwindig­keit mit der Zeit zunimmt. Genauso, wie bei der gleich­förmigen Trans­lations­bewegung die Geschwindig­keit mit der Zeit zunimmt. Und wenn man das jetzt noch einmal nach der Zeit integriert, erhält man:

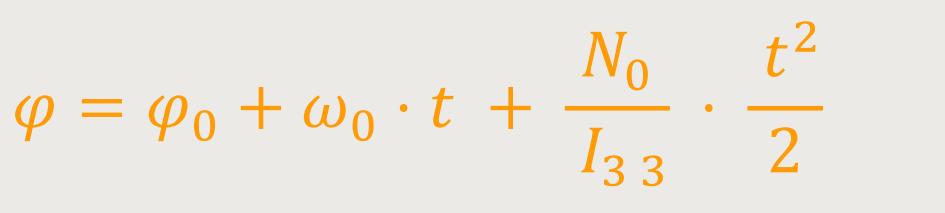
Das entspricht exakt dem normalen Fallgesetz für die Trans­lations­bewegung.

φ_₀   ist ggf. eine Anfangsbedingung
ω_₀ · t   ist auch eine Anfangsbedingung

Also, je größer das Trägheits­moment wird, desto kleiner wird die entsprechende Winkel­beschleunigung.

⇦ Kapitel Kapitel ⇨