In der nach­folgenden Betrach­tung geht es darum, dass sich ein starrer Körper in irgen­deiner Weise bewegt. Die Unter­suchung trans­latorischer Bewegungen ist auf Dauer nicht besonders interessant. Denn dort verhält es sich nicht anders, wie bei Massen­punkten. Interessant wird es dagegen, wenn wir die Rotation näher beleuchten. Insofern werden wir jetzt die Trans­lation völlig außer Acht lassen.

Wenn wir uns nun auf die Rotation beschrän­ken, dann muss es an diesem starren Körper einen festge­haltenen Punkt geben. Durch diesen Punkt geht dann auch eine Drehachse, um die sich der Körper drehen kann. So könnte es zum Beispiel auch sein, dass der Körper während der Rotations­bewegung dauernd die Lage der Dreh­achse ändert. In Wirklich­keit spiralt oder taumelt der Körper irgendwie herum.

Es lässt sich schon erahnen, dass dies in der mathe­matischen Durch­führung gar nicht so einfach ist. Wir werden hier auch nicht in alle Details der Kreisel­mechanik einsteigen. Wer sich für diesen Bereich interes­siert, sollte sich das Buch von Arnold Sommerfeld über die Kreisel­dynamik zulegen.

Dennoch werden wir einige Aspekte betrachten, weil dieses Thema mit zu den Grund­lagen der Mechanik gehört. Es kann nicht schaden zu verstehen, worauf es bei der Rotation von starren Körpern ankommt, und was man unter einem Trägheits­moment versteht. Das sind Dinge, die auch in der Alltags­welt eine große Bedeutung haben und die für viele praktische Anwendungen wichtig sind.

Hierzu wählt man sich wieder ein orthonormales Bezugssystem _x, _y, _z, welches fest im Raum steht. Das heißt, es handelt sich wieder um ein Inertial­system. Und die Rotation dieses starren Körpers erfolgt jetzt relativ zu diesem Inertial­system mit einem Winkel­geschwindig­keits­vektor . Wobei sich im Laufe der Zeit die Dreh­achse während der Rotation relativ zu dem ruhenden Inertial­system zeitlich verändern kann.

Wie wir wissen, ist die Bewegung eines Massen­elementes bzw. eines sich drehenden starren Körpers gegeben als:

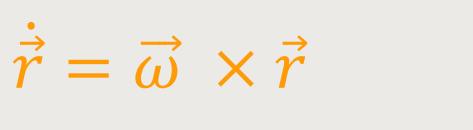
Auf diese Beziehung sind wir schon des Öfteren gestoßen, und wir kennen sie insbesondere aus der Betrachtung der Kreis­bewegung. Letzten Endes haben wir es bei der Rotation eines starren Körpers ständig mit einer Kreis­bewegung zu tun. Denn jeder Massen­punkt dieses starren Körpers bewegt sich auf einer Kreis­bahn. Es wird nur etwas kompli­zierter, wenn sich die Richtung des Winkel­geschwindig­keits­vektors während der Bewegung ändert.

Bei vorge­gebenem Winkel­geschwindig­keits­vektor und Orts­vektor ergibt sich die Geschwindig­keit wie beschrieben. Man legt also den Ursprung des Koordinaten­systems in den festge­haltenen Punkt des rotierenden starren Körpers. Das Koordinaten­system ist damit raumfest und ruht relativ zu dem Inertial­system. Und relativ zum Inertial­system rotiert dann auch der starre Körper.

Die Gleichung, die diese Rotation beschreibt, ist die Bewegungs­gleichung und ist analog zu dem, was wir bereits aus der Punkt­mechanik für transla­torische Bewegungen kennen. Dort wurde das Newton-Axiom betrachtet, dass nämlich die Kraft die Ursache einer zeit­lichen Ände­rung des Impulses ist.

Bei der Rotation lautet jetzt die Gleichung:
Drehmoment = zeitliche Änderung des Drehimpulses

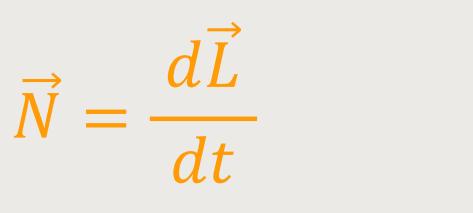
Das ist die Grund­gleichung die es zu lösen gilt.

Zunächst geht es darum, eine Möglich­keit zu finden, den Dreh­impuls leicht auszu­rechnen. Beim normalen Impuls war dies relativ einfach. Es wäre von Vorteil, wenn auch der Dreh­impuls mit einer relevanten Geschwindig­keits­größe zusammen hängt.

In ähn­licher Weise lässt sich sagen, was bei der Trans­lation die Geschwindig­keit ist, das ist bei der Rotation die Winkel­geschwindig­keit. Man benötigt demnach einen Zusammen­hang zwischen und . Bei der Trans­lation ist die Situation so, dass der Impuls und die Geschwindig­keit immer parallel zueinander sind. Daher genügt ein Faktor dazwischen (z.B. p = m · v). Nun ist es aber so, dass und im Allge­meinen nicht parallel zuein­ander sind. Dennoch lässt sich der Gesamt­dreh­impuls eines starren Körpers ausrechnen.

Der Gesamt­dreh­impuls ist jetzt die Summe über die Einzel­dreh­impulse aller Massen­elemente dm aus denen der ganze starre Körper besteht. Hierzu integriert man über das gesamte Volumen:

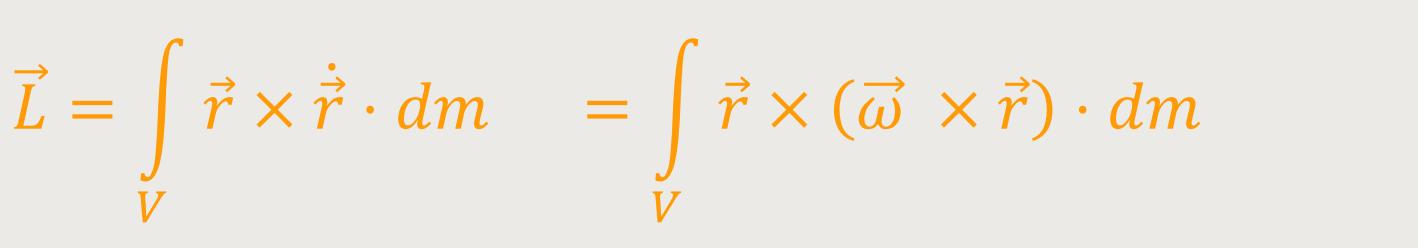
· dm   ist der Impuls des Massen­elementes

Eine Rechenregel aus der Vektor­rechnung besagt:

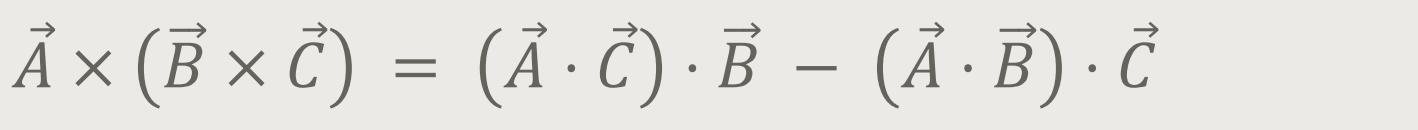
Damit ergibt sich:

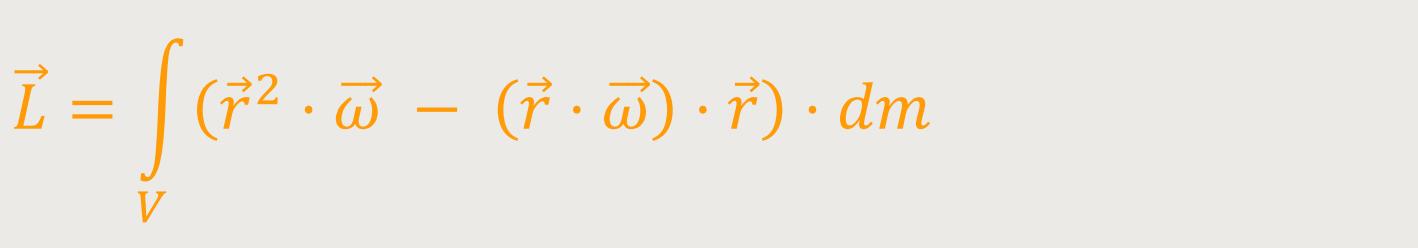
Was letztlich dabei heraus­kommt ist der Trägheits­tensor. Wir werden weiter unten nochmals darauf eingehen.

Es gibt Beziehungen, die man am besten dadurch löst, indem man sie in Komponenten aufschreibt. Denn obige Beziehung lässt sich nicht so ohne weiteres umformen. Deshalb schreibt man die einzelnen Komponenten des Dreh­impuls­vektors der Reihe nach auf. Auf diese Weise erhält man die Komponenten L_₁ , L_₂ und L_₃.

In „Komponenten­schreib­weise” würde es zum Beispiel so aussehen:

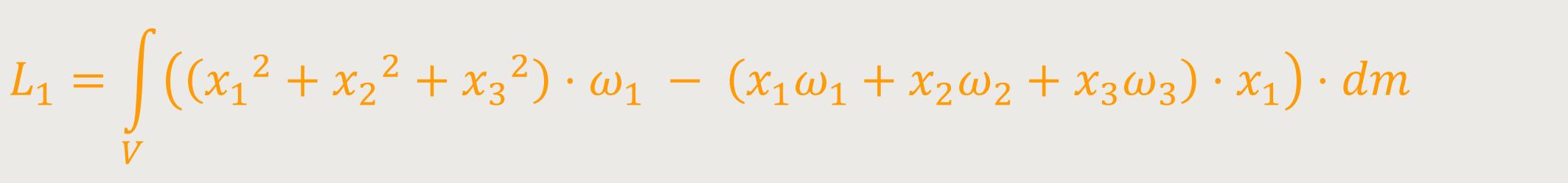
Zunächst sieht das noch sehr unüber­sicht­lich aus. Aber diese Vorgehens­weise ist notwendig, um anschlie­ßend weiter umformen zu können. Die Idee ist dabei, dass man den Zusammen­hang zwischen und herstellt. Es wäre also schön, wenn es gelingt, aus der Beziehung das herauszuholen.

Aus diesem Grund wird die Komponente L_₁ so formuliert, dass man Rechen­faktoren von erhält. Dabei überlegt man sich zunächst, welche Terme ω_₁ , ω_₂ und ω_₃ enthalten.

Nach der Umstellung von L_₁ erhält man:

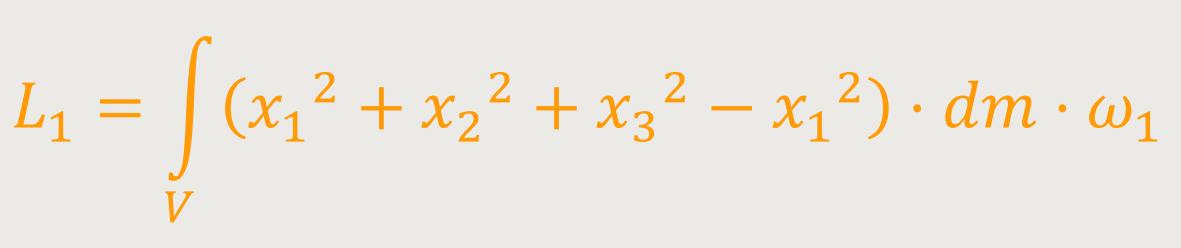
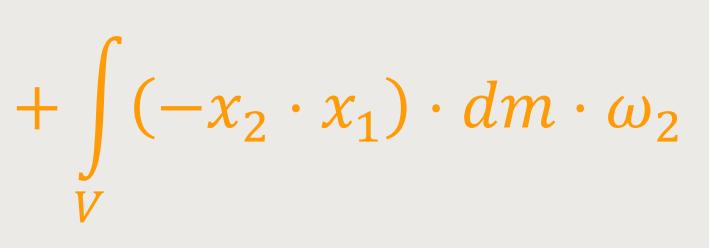
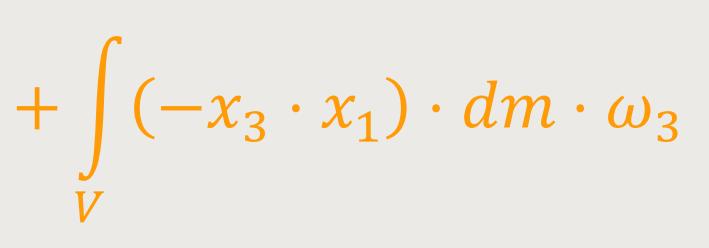
Hinweis: Der Winkel­geschwindig­keits­vektor 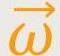ist im gesamten Raum überall der Gleiche. Somit ist er für die Integration über das Volumen des Körpers eine Konstante und kann aus dem Intergral heraus­geholt werden.

Analog ergibt sich für die zweite Komponente:

Nach der Umstellung von L_₂ erhält man:

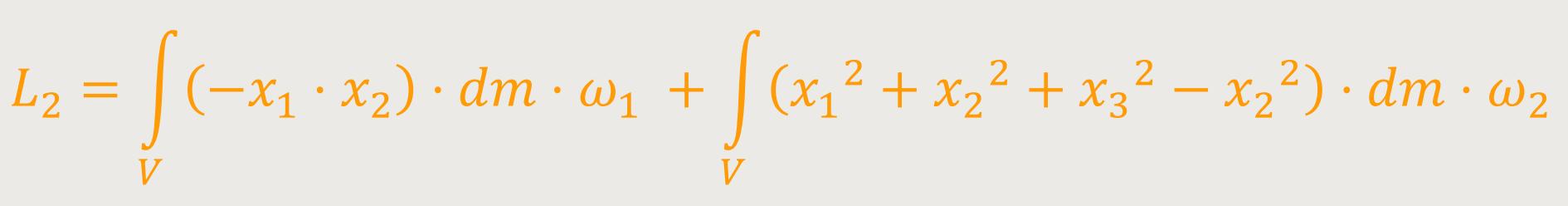
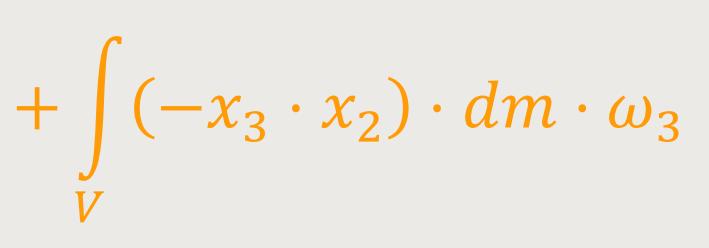
Analog ergibt sich für die dritte Komponente:

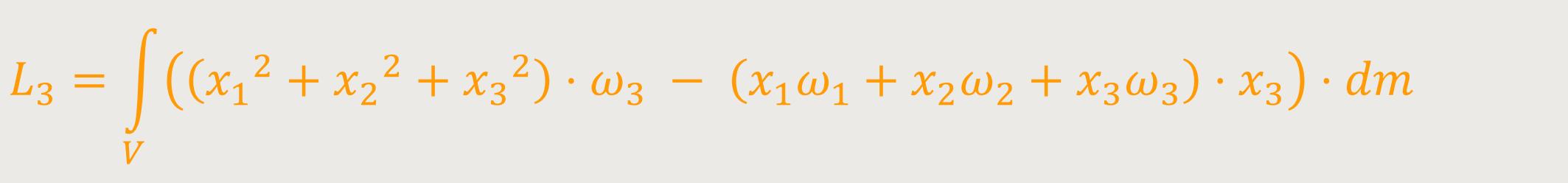
Nach der Umstellung von L_₃ erhält man:

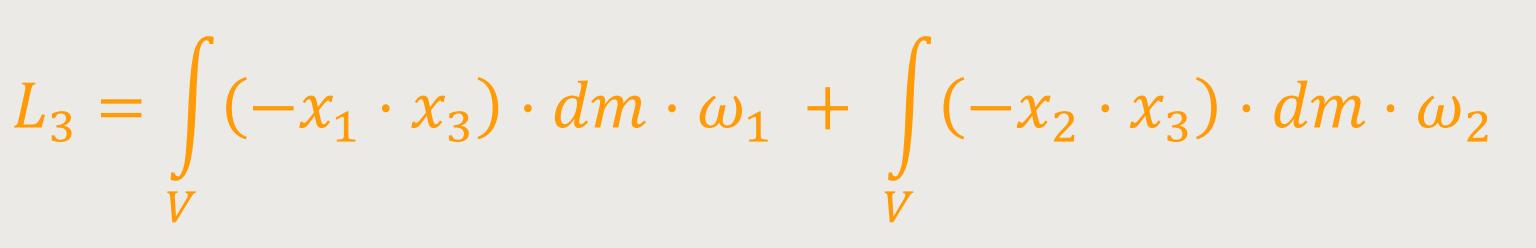
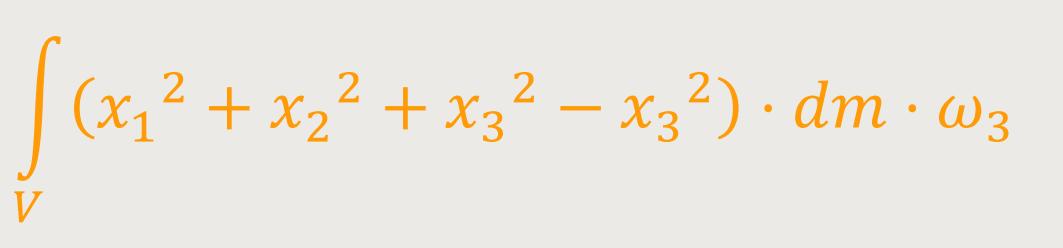
Hinweis: Mit obigen Inte­gralen wird nur ange­deutet, dass man den Körper in viele kleine Massen­elemente zerlegt und auf alles aufsummiert. Ob es dann mathe­matische Methoden gibt, wie man das besonders geschickt machen kann, steht auf einem anderen Blatt.

Bei näherer Betrachtung kann man erkennen, dass sich die Inte­grale als Faktoren heraus­bilden. Diese Rechen­faktoren ergeben sich alle durch Inte­gration über die entspre­chende Form des Körpers. Wobei letztlich auch dessen Dichte eingehen kann, wenn man statt dm = ϱ · dV schreibt. Je nach Körper, Dichte und Form kriegt man entspre­chende Inte­grale heraus.

Nun liegt es nahe, die Matrizen­schreib­weise anzu­wenden. Eine Matrix ist eine quadra­tische Anord­nung von Zahlen. Und in der Physik finden vor allen die quadra­tischen Matrizen Anwen­dung. Da wir uns im 3-dimensionalen Raum befinden, wird das eine 3·3 Matrix sein.

Alles, was man oben so aufwendig als Integrale geschrieben hat, kann man ganz einfach in Form einer „Matrize” darstellen. Dabei gilt für die I-Indizes: Erstes Indizes steht für die Zeile, zweites Indizes steht für die Spalte:

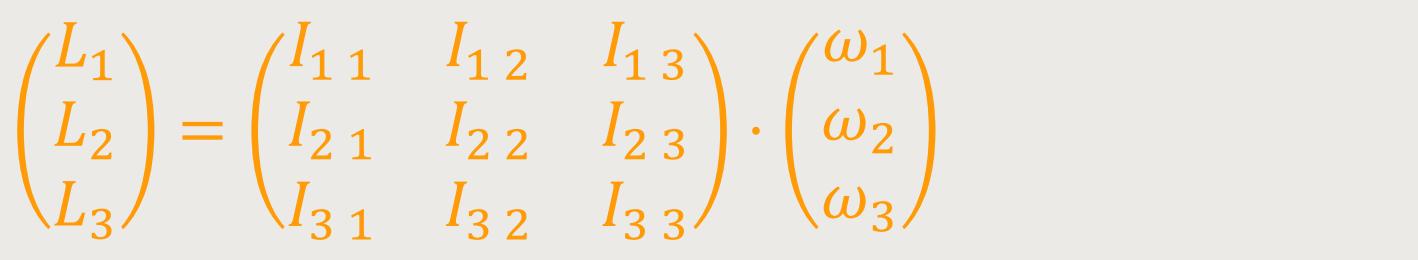
_L₁, _L₂ , _L₃   sind die Komponenten des Drehimpulsvektors

Warum diese Vorgehens­weise? Dazu muss man wissen, wie man eine Matrix ( hier 3·3 Matrixelemente ) mit einem Vektor multi­pliziert.

L1 = Erste  Zeile (Matrix) ∗ letzte Spalte (Faktor)
L2 = Zweite Zeile (Matrix) ∗ letzte Spalte (Faktor)
L3 = Dritte  Zeile (Matrix) ∗ letzte Spalte (Faktor)

Daraus folgt:

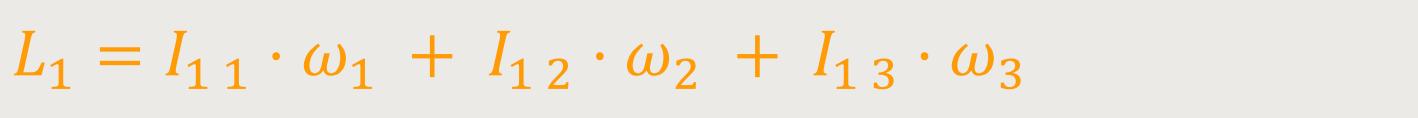
Die Physiker sind im Allge­meinen daran interes­siert, alles so effizient wie möglich aufzu­schreiben. Noch kürzer lässt sich das in der bereits erwähnten Tensor-Schreib­weise darlegen.

In der „Tensor-Schreib­weise” stellt man die i-te Komponente des Dreh­impuls­vektors heraus:

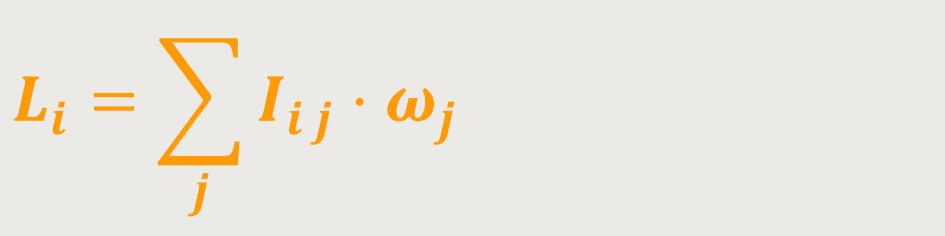
Hier ist „i” ein frei zu wählender Index.

Zum Beispiel wählt man i = 1, das ent­spricht L_₁. Anschlie­ßend summiert man über j. Daraus ergibt sich:

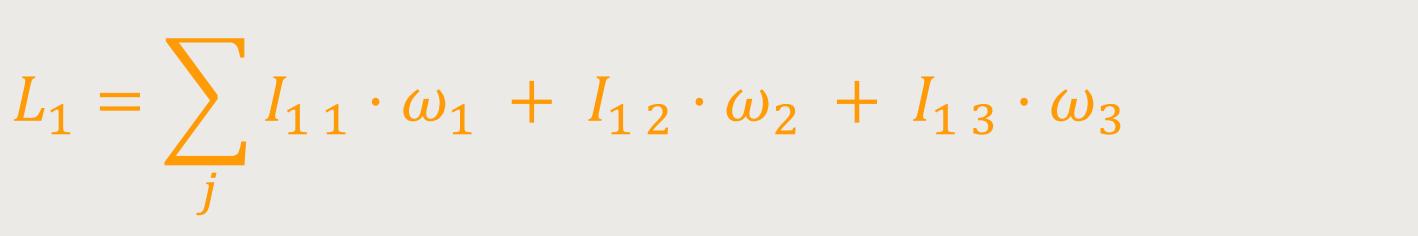
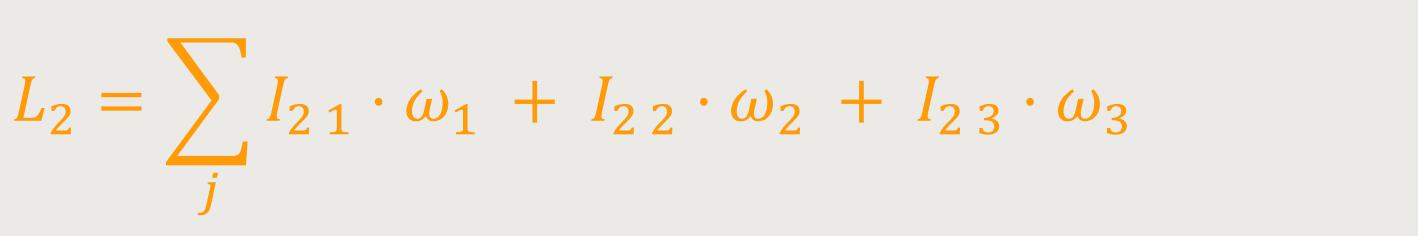
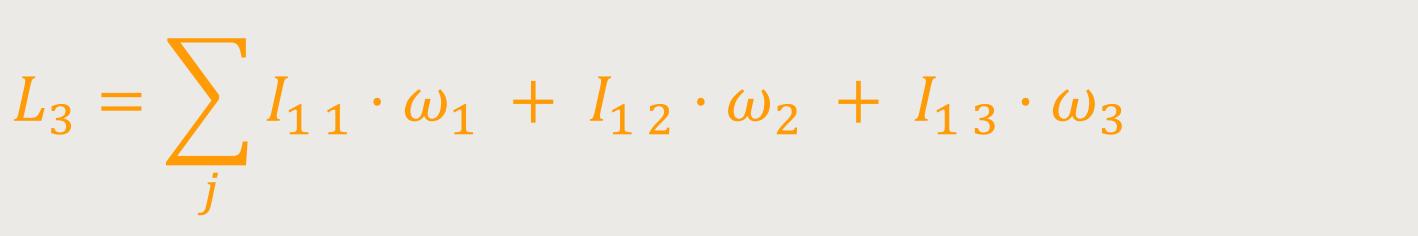
Diese Schreib­weise ist für Physiker noch nicht kurz genug. Wenn bei Index­schreib­weisen und Gleichungen Summen vorkommen, schreibt man diese gar nicht hin. Und wenn in einem Produkt von zwei indizierten Größen zwei Indizes gleich sind, bedeutet das wiederum, dass über die Indizes von 1 bis zur Dimensions­zahl (hier 3) summiert wird.

Alles, was man oben aufwendig formuliert hat, lässt sich dann durch eine einfache Beziehung ausdrücken:

Wenn man eine solche Schreib­weise sieht, bei der in einem Produkt zwei Indizes als gleich bezeichnet sind, dann summiert man über sie, indem man sich das Summen­zeichen wieder hinzu denkt. Das Summen­zeichen bleibt nach wie vor wirksam, es wird nur vereinfacht ausgedrückt.

Natürlich lässt sich das auch anders formulieren:

In der Matrix-Schreib­weise lautet dies:

Dieser Ausdruck steht für die gesamte Matrix. Und die 3·3 Matrix ist der Trägheits­tensor. In der gesamten Matrix sind die Trägheits­momente und die Richt­momente enthalten.

Und damit erhält man jetzt einen Zusammen­hang zwischen und .

I_{i j}   ist der Trägheitstensor

I_{₁ ₁} , I_{₁ ₂} und I_{₁ ₃} sind die Trägheitsmomente (Elemente in der Hauptdiagonale der Matrix)
I_{₁ ₂} , I_{₁ ₃} und I_{₂ ₃} sind die sogenannten Richtmomente oder Trägheitsprodukte.

Ein Vergleich mit dem bisher Erarbeiteten ergibt folgendes für die Trägheits­momente:

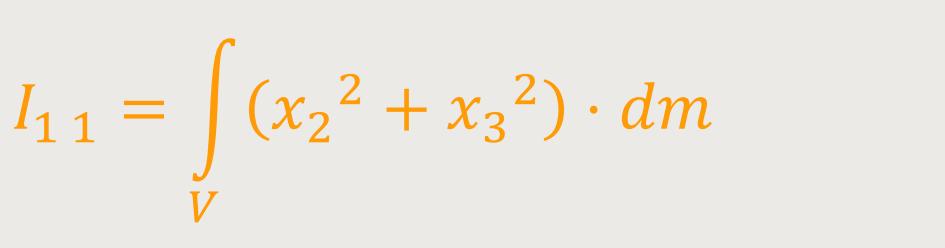
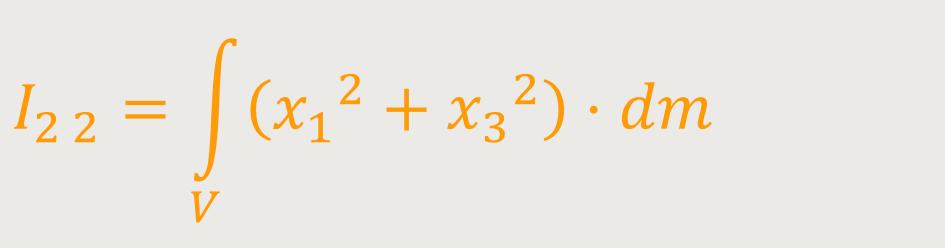
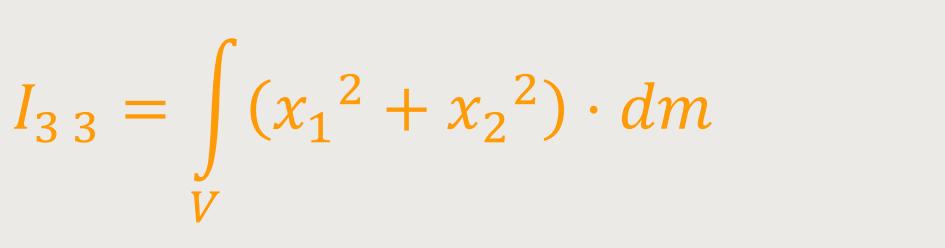
Und für die Trägheits­produkte folgt daraus:

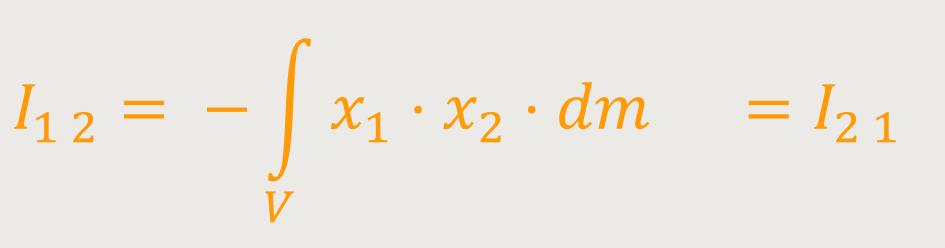
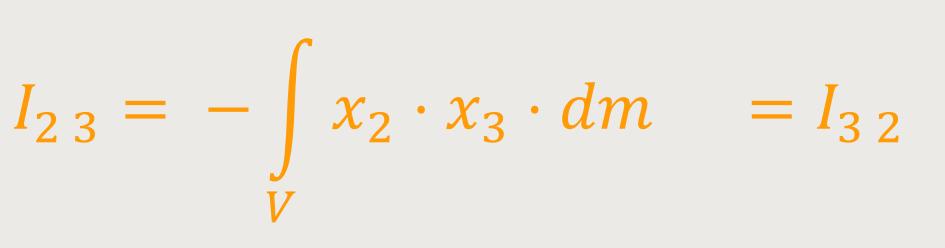
Und damit erkennt man sofort, dass der Trägheits­tensor symmetrisch ist. Das heißt, man benötigt gar nicht alle neun, es genügen sechs.

⇦ Kapitel Kapitel ⇨