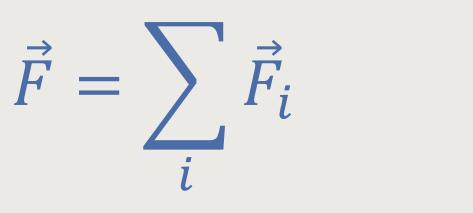Jetzt werden wir erst­mals das Massen­punkt­modell verlassen. Bisher hatten wir im Wesent­lichen nur die Punkt­mechanik behandelt. Entweder wurden ein oder mehrere einzelne Masse­teilchen betrachtet. Aber die Welt um uns herum besteht über­wiegend aus makro­skopischen Körpern. Deswegen wollen wir uns jetzt mit ausge­dehnten Körpern beschäf­tigen. Diese Körper sollen im weiteren Verlauf nicht verformbar sein, also „starr”. Im Gegen­satz dazu gibt es auch die verform­baren Körper. Dabei handelt es sich entweder um elastisch verform­bare Festkörper oder um Fluide, Flüssig­keiten und Gase.

Als Erstes betrachten wir nicht verform­bare, starre Körper. Wobei das Ganze natür­lich wieder eine Ideali­sierung ist. Denn wenn man eine genü­gend große Kraft auf einen Körper ausübt, wird sich dieser immer verformen. Wir schränken jedoch den Bereich der Kräfte ein, indem wir die Form­änderung des festen Körpers so gering halten, dass man den Körper in guter Näherung als nicht verform­bar betrachten kann.

Ein „starrer Körper” lässt keine Ände­rung seiner Form zu. Man sagt auch, er ist nicht deformier­bar. Bei diesen makros­kopischen Körpern tritt gegen­über den Massen­punkten ein neuer Aspekt auf. Diese Körper können sich einer­seits wie die Massen­punkte trans­latorisch fort­bewegen. Aber sie können auch um eine Achse rotieren. Im weiteren Verlauf werden wir deshalb auch auf die Rotationen von solchen starren Körpern näher eingehen. Und das führt uns dann letzten Endes auf die Kreisel­bewegung.

Ein Kreisel ist auch ein starrer Körper, der sich um eine Achse dreht. Meistens geht diese Dreh­achse durch seinen Schwer­punkt. In diesem Fall kommen Aspekte zum Tragen, die bei der reinen Trans­lation von Massen­punkten noch nicht von Bedeu­tung waren. Bei der Rota­tion hat man es dann mit mehr Frei­heits­graden zu tun, als dies bei den reinen Massen­punkten der Fall war. Denn Massen­punkte können definitions­gemäß nicht rotieren, weil sie keine nennens­werte innere Struktur haben. Dort spielt der Begriff der Rotation keine Rolle.

Anders verhält es sich bei einem ausge­dehnten starren Körper. Zusätz­lich zu den 3 bekannten Dimen­sionen der Trans­lation, sprich den 3 Freiheits­graden, kommen bei starren Körpern 3 weitere Frei­heits­grade hinzu. Diese zusätz­lichen Frei­heits­grade betreffen die Möglich­keit, um die drei verschie­denen Raumachsen zu rotieren. Letzt­lich geht es dann also insgesamt um 6 Freiheits­grade.

Dennoch werden wir uns gedank­lich einen starren Körper als zusammen­gesetzt aus einzelnen Massen­punkten vorstellen, oder aus einze­lnen Volumen- bzw. Massen­elementen. Dadurch behalten wir den Bezug zu der uns bekannten Punkt­mechanik. Anschließend muss man nur noch über diese einzelnen Massen­punkte aufsummieren, um das Verhalten des gesamten Körpers beschreiben zu können. Und da werden wir in weiterer Folge in zwei Schritten vorgehen.

Auf der einen Seite ist es zwar interessant, die Bewegungen von starren Körpern unter dem Einfluss von Kräften und Dreh­momenten zu unter­suchen. Aber ander­seits ist es in vielen Fällen auch erforder­lich, die „Statik” von starren Körpern zu betrachten. Da geht es dann um die Frage, unter welchen Voraus­setzungen wird denn ein starrer Körper im Gleich­gewicht sein, also statisch bleiben. Insbe­sondere wenn unter­schiedliche Kräfte an ihm angreifen.

Wir werden generell einen starren Körper auf der Basis der Punkt­mechanik beschreiben. Wie schon erwähnt, geht man davon aus, dass der Körper aus N Teilchen, also Molekülen bzw. Volumen­elementen besteht, die starr mit­einander verbunden sind. Und die Positionen jedes dieser Teil­chen wird durch verschie­dene Orts­vektoren _i beschrieben. Jedes Teilchen hat natür­lich auch eine gewisse Masse m_i. Und zusammen­gesetzt aus diesen Massen­elementen denkt man sich dann diesen starren Körper.

Wichtig ist auch, dass so ein Körper ein Gesamt­volumen V hat, denn man betrachtet ja etwas Makros­kopisches. Und aus allen Volumina von einzelnen Massen­teilchen wird schließ­lich eine Summe über alle Volumen­elemente V_i gebildet. Oder wenn man es als Integral schreibt, ergibt sich:

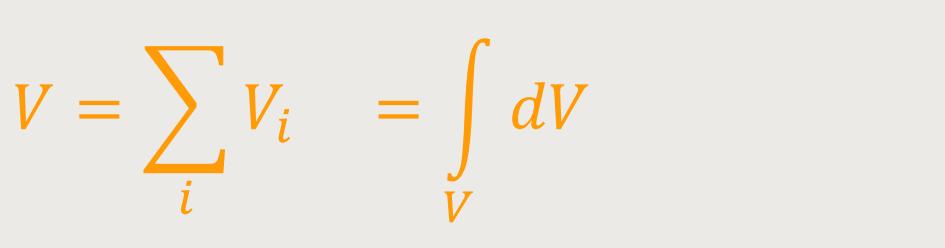
dV   sind die Teilvolumina

Neben dem Volumen ist auch die gesamte Masse wichtig:

dm = ϱ · dV   (Massenelement = Dichte · Volumenelement)

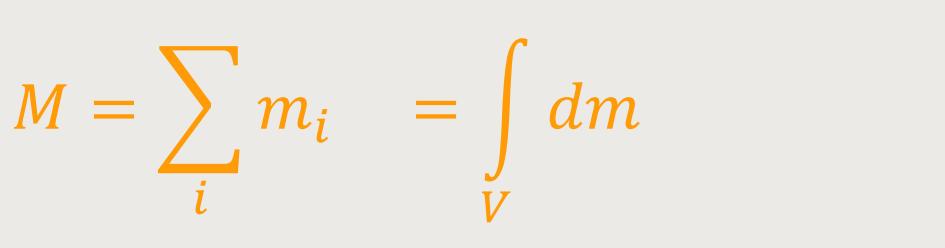
Nachdem wir uns einen kurzen Über­blick verschafft haben, betrachten wir zunächst die Statik starrer Köper.

Also, wir gehen davon aus, dass auf einen solchen starren Körper eine oder mehrere Kräfte angreifen. Wenn nun eine solche Kraft auf einen starren Körper angreift, dann verfolgt man das Ziel, diese Kraft­wirkung zu charakte­risieren. Und hier erweist es sich als zweck­mäßig, zusätz­lich zu dem Kraft­vektor auch den Vektor des Dreh­moments _B mit einzu­beziehen. Wobei man diese Kraft nicht vom Koordinaten­ursprung aus betrachtet, sondern bezüg­lich eines vorge­gebenen fest gewählten Bezugs­punktes B.

Und dieses Dreh­moment bezüg­lich dieses fest gewählten Bezugs­punktes ist gleich dem Vektor zwischen dem Angriffs­punkt der Kraft und dem Bezugs­punkt. Beschrieben wird er durch den Orts­vektor _B des Bezugs­punktes:

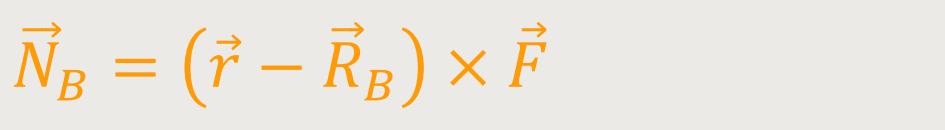
Je nach Erforder­nissen kann der Bezugs­punkt unter­schied­lich gewählt werden. Der Bezugs­punkt ist demnach nicht zwingend der Ursprung des Koordinaten­systems. Wählt man einen anderen Bezugs­punkt, dann kommt es immer auf den Verbindungs­vektor an. In unsrem Fall nicht vom Ursprung des Koordinaten­systems, sondern vom Bezugs­punkt bis hin zum Angriffs­punkt der Kraft.

Betrachtet man einen beliebig geformten starren Körper, stellt es sich wie folgt dar:

Das Drehmoment _B bleibt unver­ändert, wenn der Angriffs­punkt der Kraft längs der Angriffs­linie verschoben wird. Das nennt man auch die „Linien­flüchtig­keit der Kräfte”. Ände­rungen des Dreh­moments werden sich nur dann ergeben, wenn man die Angriffs­linie verlässt.

Wenn mehrere Kräfte _i an einem Körper angreifen, dann sind diese nur dann gleich­wertig mit der Summe all dieser Kräfte, wenn man sie sich so denken kann, als würden sie an einem gemein­samen Angriffs­punkt angreifen. Das heißt, man schaut sich die Wirkungs­linien von all diesen verschie­denen Kräften genau an.

Sollten sich womög­lich alle Wirkungs­linien in einem Punkt schneiden, können alle diese Kräfte zu diesem Punkt hin verschoben werden. In diesem Fall ergibt sich auto­matisch, dass die gemeinsame Wirkung all dieser Kräfte gleich­wertig ist zu der Wirkung der Gesamt­kraft, die an dem gemein­samen Punkt angreift.

Aber im Allge­meinen wird das nicht der Fall sein. Denn im 3-dimensionalen Raum können sich diese Wirkungs­linien auch verfehlen. Und dann ist es gar nicht möglich, die entspre­chenden Kräfte _i so zu verschieben, dass sie sich alle zu einem gemein­samen Schnitt­punkt aller Wirkungs­linien vereinen lassen.

In der Praxis hat man eine etwas allge­meinere Formu­lierung gefunden die es ermöglicht, Unter­suchungen anzu­stellen, auch für den Fall, dass man mehrere Kräfte hat die so liegen, dass ihre Angriffs­linien nicht alle durch ein und denselben Punkt gehen. In diesem Fall ersetzt man einfach die Kräfte durch eine Summen­kraft, die an einem gemein­samen Angriffs­punkt angreift. Aus diesem Grund wird die Wirkung aller Kräfte _i wie folgt definiert:

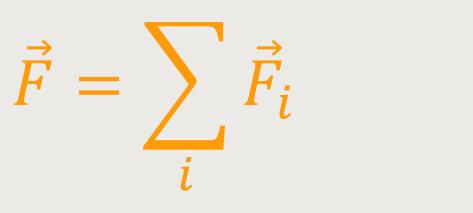
Als gemein­samen Angriffs­punkt wird nach wie vor der Bezugs­punkt B gewählt. Man betrachtet die Summe aller angrei­fenden Kräfte zunächst einmal unab­hängig davon, wo sie angreifen und lässt die Summe aller Kräfte an dem gemein­samen Angriffs­punkt B angreifen. In ähn­licher Weise lässt sich auch das gesamte Dreh­moment verall­gemeinern:

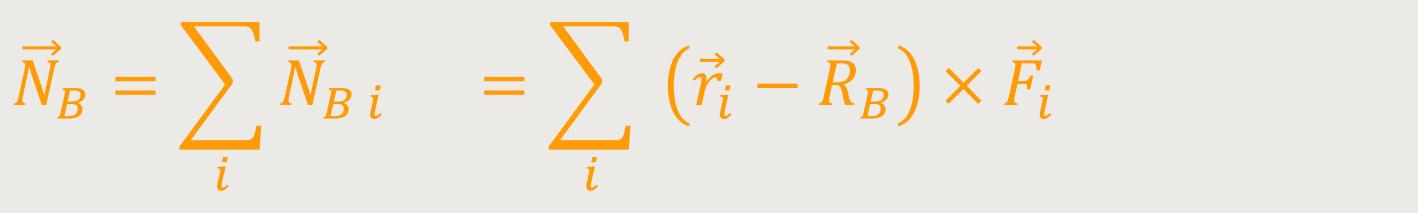
Man kann auch schreiben:

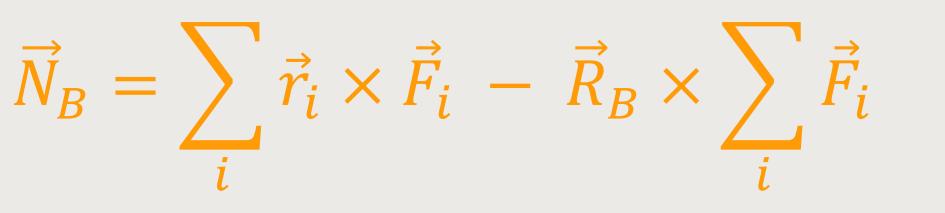
So ergibt sich einer­seits die gesamte Kraft und anderer­seits auch das gesamte Dreh­moment. Diese beiden charakte­risieren die Wirkung der aller Kräfte.

Hierbei ist es wichtig, dass die gesamte Kraft an dem Bezugs­punkt angreift. Das hat zur Folge, dass diese Gesamt­kraft als Vektor­summe der einzelnen Kräfte, bezüglich dieses Bezugs­punktes, letztlich gar kein Dreh­moment bewirkt. Denn wenn man eine Kraft am Bezugs­punkt angreifen lässt, dann ist das Dreh­moment, welches dadurch bewirkt wird gleich Null, weil der Verbindungs­vektor zum Nullvektor wird.

Dement­sprechend verursacht eine Kraft, die am Bezugs­punkt angreift, kein Dreh­moment. Das heißt, die Gesamt­kraft am Bezugs­punkt trägt nichts zu diesem Dreh­moment bei. Sondern nur die Einzel­kräfte haben bezüg­lich des Bezugs­punktes entspre­chende Dreh­momente. Sie werden aber insgesamt dieses Gesamt­drehmoment bewirken, und daher braucht man hier sonst nichts Weiteres zu berück­sichtigen.

Zusammen­fassend können wir sagen: Wenn etliche Kräfte _i an einem starren Körper angreifen, kann die Wirkung all dieser Kräfte charakte­risiert werden, einer­seits durch die Vektor­summe aller Kräfte, die man sich angreifend denkt, an dem jeweils vorge­wählten Bezugs­punkt B. Aber auch durch das gesamte Dreh­moment aller einzelnen Kräfte in Bezug auf den vorge­wählten Bezugs­punkt B.

Natürlich hängt das im Wesent­lichen davon ab, was für einen Bezugs­punkt man wählt. Und das Schöne daran ist, dass man die Frei­heit hat, ihn nach Bedarf frei zu wählen. Wir werden sehen, was das für einen Vorteil bringt, wenn dieser Bezugs­punkt B vorge­wählt werden kann. Hierzu werden wir zwei Situationen gegen­überstellen.

Im ersten Fall sei die Summe aller Kräfte ≠ 0 :

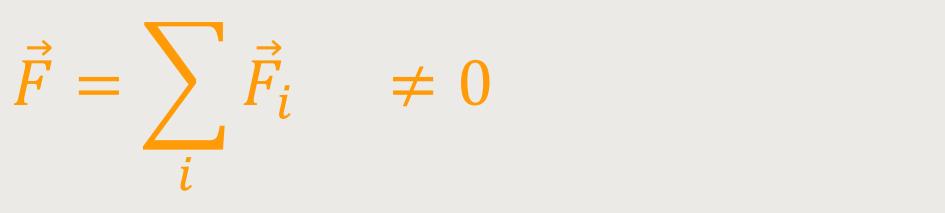
Wenn wir noch­mals obigen Ausdruck für das Gesamt­dreh­moment heranziehen, dann können wir erkennen, dass man den Ort des Bezugs­punktes immer so wählen kann, dass die Differenz der beiden Terme gerade gleich Null ist. Man kann das _B so wählen, dass die gesamte Kraft gerade den ersten Term kompen­siert, und damit das gesamte Dreh­moment gleich Null wird.

Also, man kann den Bezugs­punkt B, der zugleich auch der Angriffs­punkt der Summen­kraft ist so wählen, dass das gesamte Dreh­moment _B = entspricht. Das ist sehr vorteil­haft, weil die Wirkung aller Kräfte einzig und allein durch die Summen­kraft darge­stellt wird und es zusätz­lich kein Dreh­moment mehr gibt.

Mit anderen Worten, alle diese Kräfte _i, die separat an dem Körper angreifen sind gleich­wertig mit der Summen­kraft, die an dem Bezugs­punkt angreift. Und da das Dreh­moment gleich Null ist, muss dieses Dreh­moment nicht mehr separat berücksichtigt werden. Alle diese _i sind gleich­wertig mit der zuvor erwähnten in B angreifenden Gesamt­kraft:

Wie wählt man aber diesen Bezugs­punkt, sodass dieses Dreh­moment gleich Null wird. Das lässt sich an einem ein­fachen Beispiel zeigen. Nehmen wir an, die Schwer­kraft wirkt auf einen starren Körper. Das bedeutet, dass jedes einzelne Massen­element eine Gewichts­kraft _i erfährt:

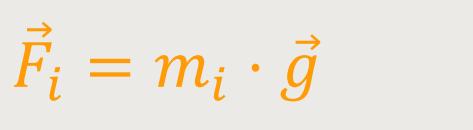
Jetzt muss man den Bezugs­punkt bzw. Angriffs­punkt der Gesamt­kraft so wählen, dass die Gesamt­kraft gleich­wertig wird zu der Wirkung aller Einzel­kräfte _i, damit das gesamte Dreh­moment gleich Null ist. Daraus ergibt sich formal für das Gesamt­dreh­moment:

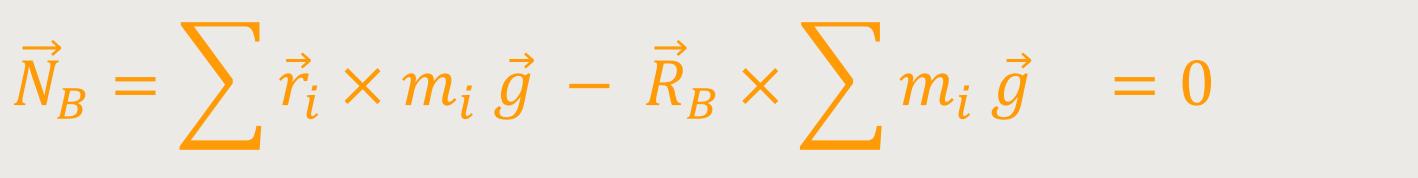
Der Zusammen­hang lässt sich auch wie folgt dar­stellen:

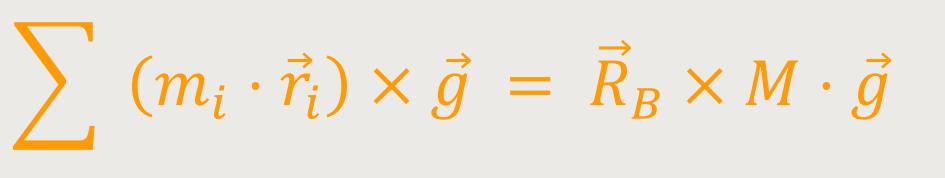
Diese Gleichung ist jeden­falls erfüllt, falls:

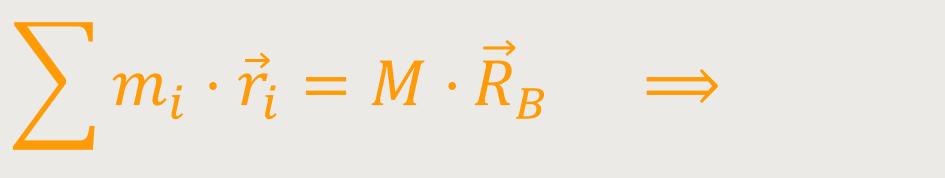
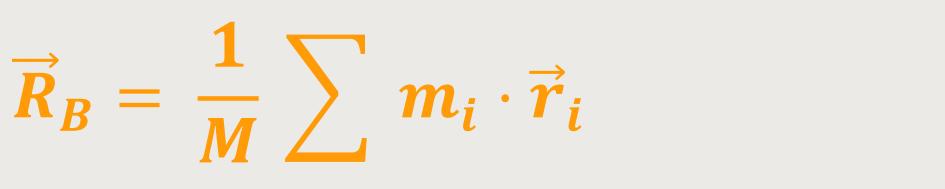
Das entspricht genau der Definition des Massen­mittel­punktes.

Wenn sich also ein ausge­dehnter starrer Körper unter der Wirkung der Schwer­kraft befindet, lässt sich die Gesamt­wirkung aller Kräfte darstellen, indem man als Angriffs­punkt den Bezugs­punkt B wählt, der dem Massen­mittel­punkt entspricht.

Deshalb nennt man bei starren Körpern den Massen­mittel­punkt auch den „Schwer­punkt”. Weil eben der Schwer­punkt derjenige Punkt ist, an welchem man sich die Gesamt­kraft, also das Gesamt­gewicht des Körpers, angreifend denkt. Dadurch wird letzt­lich das gleiche Ergebnis erzielt, als wenn alle Einzel­kräfte für sich betrachtet würden.

Oder anders ausge­drückt, wenn man diesen Körper im Gleich­gewicht halten möchte, dann muss man eine gleich große entgegen­gesetzte Kraft im Schwer­punkt angreifen lassen, um den Körper hinsicht­lich aller seiner Wirkungen kräfte­frei zu halten. Man muss dann nicht jede einzelne Kraft entspre­chend kompen­sieren, sondern es muss ledig­lich der Körper kräfte­mäßig im Schwer­punkt unter­stützt werden, wodurch sich der Körper völlig ausgleichen lässt.

Schließen wir die Betrachtung dadurch, dass wir uns anschauen, was passiert, wenn zwei „parallel gleich­gerichtete Kräfte” an einem Körper angreifen.

zum Beispiel greift an einem waage­rechten läng­lichen Körper links eine Kraft _₁ und rechts eine Kraft _₂ an. Beide Kräfte sind in unserem Beispiel parallel nach unten gerichtet. Was für eine Gesamt­kraft wird dadurch bewirkt? Hierzu denken wir uns eine Verbindungs­linie der Angriffs­punkte im rechten Winkel zu den Kraft­linien.

Das gesamte Dreh­moment soll hier wieder gleich Null sein:

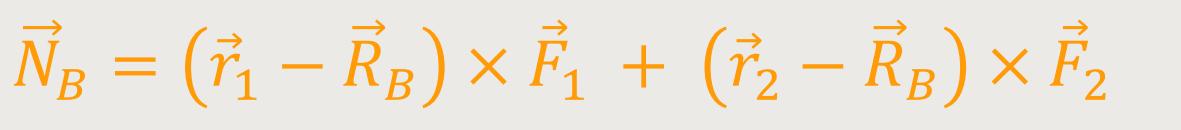
Für die Beträge erhalten wir:

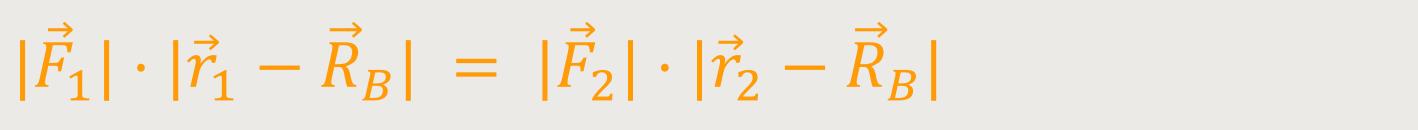
Und das besagt nichts anderes als das Hebel­gesetz:

Kraft · Kraftarm = Last · Lastarm

Hierzu muss der richtige Bezugs­punkt zwischen den beiden Kräften liegen. An der Stelle dieses Bezugs­punktes wirkt eine entgegen­gesetzt gerichtete Gesamt­kraft, die gleich der Summen­kraft der Einzel­kräfte ist. Diese entspre­chende Gegen­kraft, die im vorge­nannten Beispiel nach oben wirkt, hebt die Summen­kraft auf und lässt sich definieren als das Hebel­gesetz:

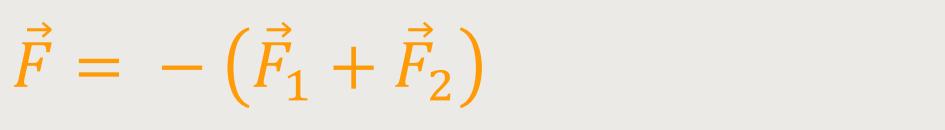
Gehen wir in unserer Betrachtung noch einen Schritt weiter.

Im zweiten Fall sei die Summe aller Kräfte = 0 :

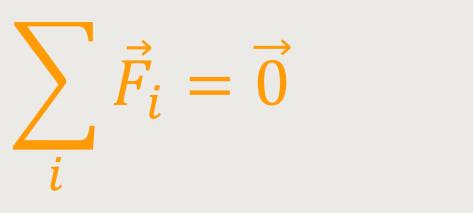
Worin besteht jetzt der Unter­schied zu vorherigem Fall? Wenn die Summe aller Kräfte gleich Null ist, dann spielt es keine Rolle wohin man den Bezugs­punkt legt. Die Kraft und die Summe aller Kräfte werden dann immer gleich Null sein. Das macht die Sache sehr über­sichtlich. Für das Dreh­moment spielt es nämlich keine Rolle, auf welchen Bezugs­punkt man es bezieht. Das ist insbesondere dann ein Fall, wenn man ein Kräfte­paar betrachtet, deren Kräfte einfach entgegen­gesetzt gleich groß sind.

Das Dreh­moment, welches diesem Kräfte­paar entspricht, lässt sich anlog zu oben wie folgt definieren:

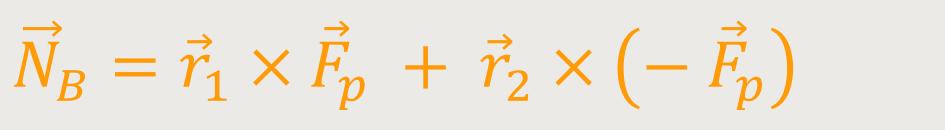
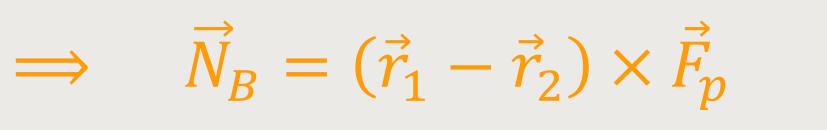
Man kann sofort erkennen, dass man nicht auf die Wahl des Ursprungs oder irgend­eines Bezugs­punktes ange­wiesen ist. Es geht einzig und allein nur um den Verbindungs­vektor. Und deswegen ist bei einem solchen Kräfte­paar ein Dreh­moment eindeutig definiert.

⇦ Kapitel Kapitel ⇨