Jetzt soll sich das System S^∗ mit seinem Ursprung O^∗ „gleich­förmig beschleunigt” relativ zum Bezugs­system S und dessen Ursprung O bewegen. Also mit konstanter Beschleu­nigung 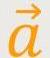. Dann ergibt sich daraus:

Wenn man integriert erhält man:

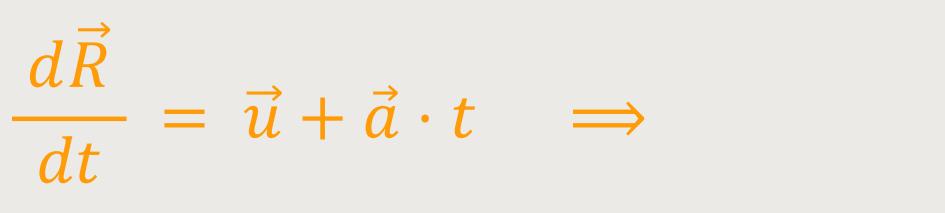
Wird noch einmal integriert kommt heraus:

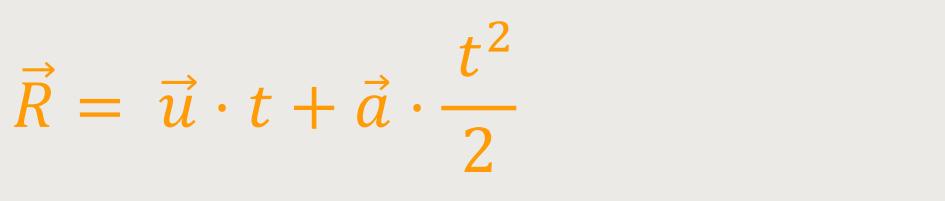
Wenn man jetzt obige Beziehung zugrunde legt, und das Argument für den Orts­vektor einsetzt, ergibt sich für das gleich­förmig beschleunigte Bezugs­system:

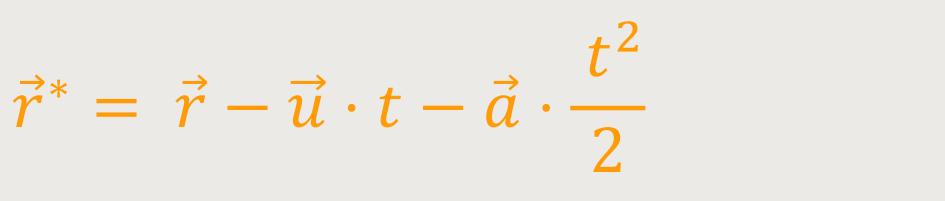
Und wieder gilt: t^∗ = t

Auch hier werden wir jetzt die dazuge­hörige Geschwindig­keit ausrechnen. Zunächst wird wieder nach der Zeit differenziert:

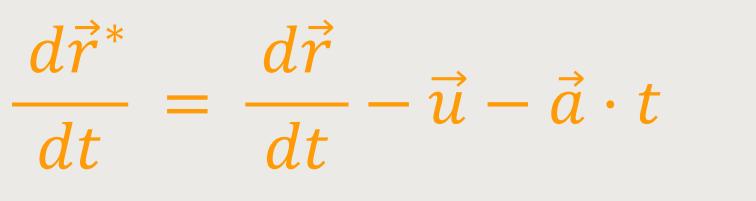
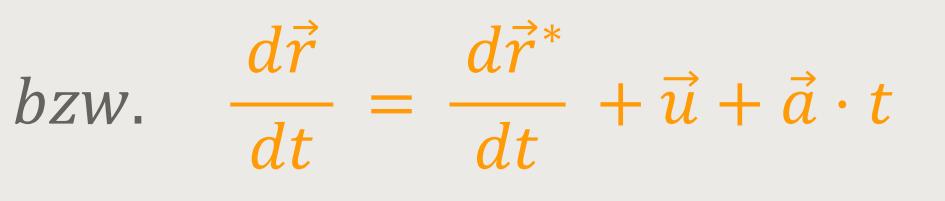
Wenn der Massenpunkt P in dem System S^∗ ruht, dann ist seine Geschwindig­keit relativ zu S. In diesem Fall is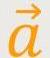t = + · t.

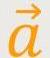Aber falls jedoch der Massen­punkt P im System S ruht, dann ist seine Geschwindig­keit relativ zu S^∗. In einem solchen Fall ist _rel = − − · t.

Nachdem wir die Geschwindig­keiten hergeleitet haben, wollen wir wieder die Beschleu­nigung ausrechnen.

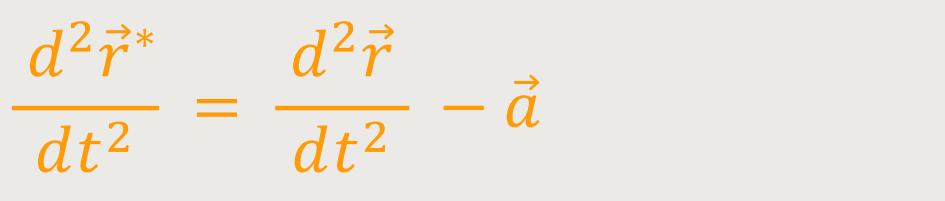
Bzw. nach Umformung erhält man:

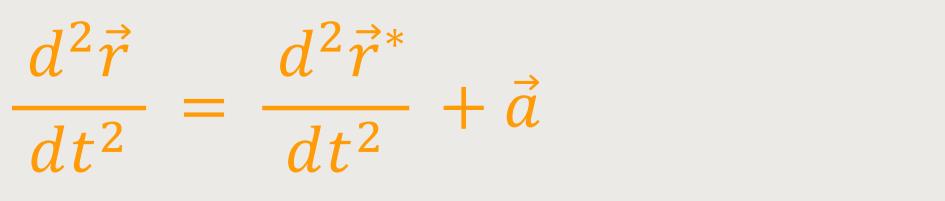
Was bedeutet das?

Wenn man das physika­lisch inter­pretiert sieht man, dass die Beschleu­nigungen jetzt nicht mehr gleich sind. Daraus folgt, dass ein „beschleunigtes” System kein Inertial­system mehr ist.

Für die Inter­pretation untersuchen wir zwei Situationen.

Im ersten Fall ist der Massen­punkt P unbeschleunigt im System S. Er kann auch ruhend sein. Was lässt sich beobachten?

Wenn das System S, wie voraus­gesetzt wird, ein Inertial­system ist und damit unbeschleunigt, dann wirken auf den Massen­punkt P offenbar keine Kräfte. Es wirken hier insbe­sondere keine „eingeprägten” Kräfte. Denn würden derartige Kräfte wirken, dann wäre der Massen­punkt relativ zum Inertial­system S beschleunigt. Denn Kraft ist ja definitions­gemäß Masse · Beschleu­nigung. Da aber jetzt keine Beschleu­nigung vorliegt, ergibt sich:

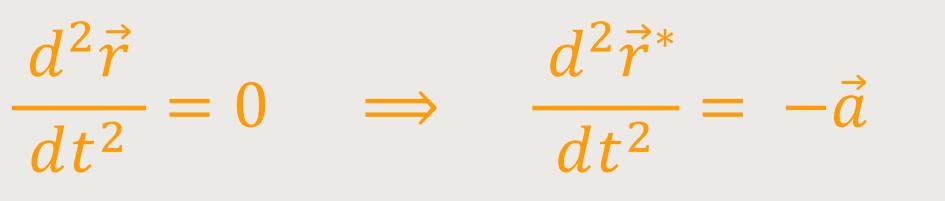
Aus Sicht des gleich­förmig beschleu­nigten Bezugs­systems erfährt dieser Körper jetzt eine Beschleu­nigung −. Natürlich wird ein Beobachter im System S keine Kraft beobachten. Aber für einen Beobachter im System S^∗ ist eine Beschleu­nigung − erkennbar. Als Beobachter macht er dafür eine Kraft verant­wortlich. Und diese Kraft ist eben Masse · Beschleunigung.

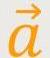
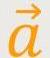
Und diese Kraft nennt man die „Trägheits­kraft” im Gegensatz zur einge­prägten Kraft.

Im zweiten Fall, ist der Massen­punkt P unbeschleunigt im System S^∗. Also gegenüber dembeschleu­nigten Bezugs­system soll der Massen­punkt unbeschleunigt sein, woraus folgt: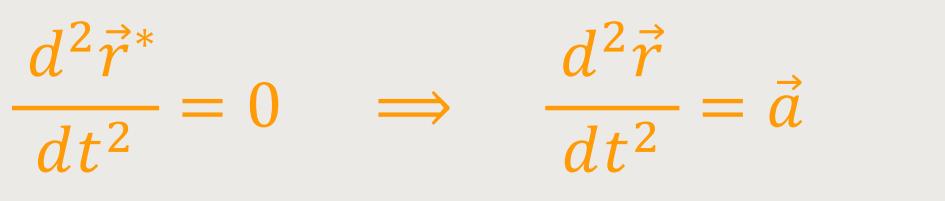

Welche Schlüsse lassen sich daraus ziehen?

Der Beobachter im System S^∗ beobachtet keine Gesamt­kraft, weil der Körper unbeschleunigt ist. Aus seiner Sicht sieht es so aus, als wenn dem Körper keine Beschleu­nigung wider­fährt. Um diesen Massen­punkt gegen S^∗ unbeschleunigt zu halten, ist jetzt eine entspre­chende Kraft erforder­lich. Man sagt, in diesem Massen­punkt muss eine „einge­prägte Kraft” wirken, die dafür sorgt, dass dieser Körper trotz­dem eine Beschleu­nigung 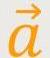erfährt. Diese Kraft bezeichnet man auch als: Masse · Beschleunigung:

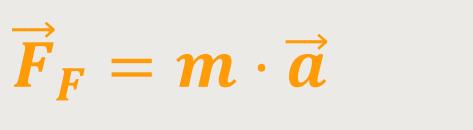
Diese Kraft bezeichnet man im Gegen­satz zur Träg­heits­kraft als eine „Führungs­kraft”. Was bedeutet das? Diese Kraft ist eine einge­prägte, wirk­liche Kraft in dem Sinne, dass sie eine Beschleu­nigung relativ zu einem Inertial­system hervor­ruft. Der Beobachter im System S nimmt nur die Führungs­kraft wahr, aber keine Träg­heits­kraft.

Die Führungs­kraft ist die Kraft, die jemand aufwendet, um einen Massen­punkt relativ zu einem beschleu­nigten System in Ruhe zu halten. In unserem Fall ist der Massen­punkt ruhend, relativ zum System S^∗. Mittels dieser Führungs­kraft wird dem Körper eine Kraft einge­prägt. Die Führungs­kraft kompen­siert quasi die Trägheits­kraft.

Ein klassisches Beispiel hierfür ist ein Koffer mit Laufrollen, in einem Zug der beschleunigt. Betrachtet man die Situation aus Sicht des Reisenden im Zug, ergibt sich folgendes:

Die Trägheits­kraft tritt auf, wenn man sich in diesem beschleu­nigten Bezugs­system befindet und man beobachtet, dass der Koffer nach hinten weg beschleunigt wird. Man macht dafür die Träg­heits­kraft verant­wortlich. Wendet man eine Führungs­kraft an, indem man den Koffer festhält, sprich um diese Träg­heits­kraft zu kompen­sieren, dann führt man diesen Massen­punkt (Koffer) mit dem beschleu­nigten Bezugs­system (Zug) mit. Aus der Sicht dieses Systems S^∗ bleibt der Massen­punkt kräftefrei, weil er ja jetzt wieder in Ruhe ist, relativ zum Zug. Aber es werden dennoch zwei Kräfte benötigt, die einander gerade kompensieren.

Betrachtet man die Situation jetzt aus Sicht eines Beobach­ters der noch auf dem Bahn­steig steht, ergibt sich verändertes Bild:

Es ist der identische Vorgang, und der Reisende im Zug hält seinen Koffer fest. Aus der Sicht des Beobach­ters auf dem Bahn­steig tritt diese Träg­heits­kraft gar nicht auf. Wohl aber sieht er in unver­änderter Form die einge­prägte Führungs­kraft auf den Koffer. Und das ist das dahinter­liegende Prinzip.

Zusammen­fassend lässt sich sagen, die einge­prägten Kräfte sind stets vorhanden. Egal in welchem Bezugs­system man sich befindet. Befindet man sich aber in beschleunigten Bezugs­systemen, treten zusätzlich die Träg­heits­kräfte auf. Und es sind genau diese Träg­heits­kräfte, die man berück­sichtigen muss, um diese scheinbar merkwür­digen Bewegungen relativ zu einem beschleu­nigten Bezugs­system in einer einheit­lichen Art und Weise zu beschreiben.

Der Haupt­punkt ist folgender: Einge­prägte Kräfte kann man durch Trans­formation auf andere Bezugs­systeme nicht wegbringen. Träg­heits­kräfte aber schon, indem man auf ein Inertial­system trans­formiert. Man begibt sich also aus einem beschleu­nigten System in ein unbeschleu­nigtes System. Aus Sicht des ruhenden Systems sind dann die Träg­heits­kräfte weg. Aber die Führungs­kraft als einge­prägte Kraft bleibt erhalten. Träg­heits­kräfte kann man durch Trans­formation auf geeignete Inertial­systeme somit zum „Verschwinden” bringen, einge­prägte Kräfte dagegen nicht. Daraus ergibt sich ein wichtiger Lehrsatz:

In einem Inertial­system gibt es keine Träg­heits­kräfte.

Doch neben transla­torischen Bezugs­systemen gibt es rotierende Bezugs­systeme, die eine Drift aufweisen.

⇦ Kapitel Kapitel ⇨