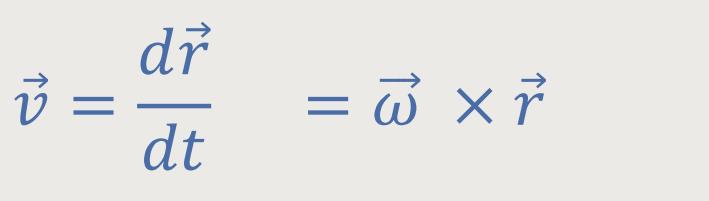Bei der nachfolgenden Betrachtung gilt zu berücksichtigen, dass jetzt „keine Translation” vorliegt.
Somit ist es sinnvoll, beide Koordinatenursprünge O und O∗ in einen gemeinsamen Ursprung zu legen. Das eine ist dann der Ursprung des Inertialsystems und das andere ist der Ursprung des rotierenden Systems. Und wie bei einem Rotationskörper üblich ist, gibt es immer eine Rotationsachse. Diese Rotationsachse hat die Eigenschaft, dass auf derselben auch die Punkte im rotierenden System in Ruhe bleiben. Und natürlich befinden sich auch die zwei Ursprünge O und O∗ auf der Rotationsachse.
Die Koordinatenachsen der Bezugssysteme müssen nicht zwingend mit der Rotationsachse parallel oder im rechten Winkel angeordnet sein. Sie können alle irgendwie schief im Raum liegen. Es wird keine bestimmte Koordinatenachse benötigt, um die das System rotiert. Rotiert wird vielmehr um den Winkelgeschwindigkeitsvektor (siehe Kapitel Kreisbewegung).
Ein wesentlicher Unterschied zur Translation besteht darin, das der Ortsvektor
 =
=
 ∗ entspricht.
Aus Sicht des Systems S und S∗
ist der Ortsvektor der gleiche.
∗ entspricht.
Aus Sicht des Systems S und S∗
ist der Ortsvektor der gleiche.
Um das näher zu beschreiben, betrachtet man das rotierende System
S∗. Das ruhende System S ist,
wie gesagt, das Inertialsystem. Aus der Sicht dieses ruhenden Systems sieht man, wie
sich die Basisvektoren des rotierenden Systems bewegen werden. Die Spitze des
Basisvektors, zum Beispiel
 x∗
x∗
Was ist dann die zeitliche Ableitung vom Vektor
 x∗?
x∗?
 x∗
x∗
Jetzt betrachten wir die zeitliche Änderung der Basisvektoren des rotierenden Systems relativ zu dem ruhenden Inertialsystem. Ganz analog erhält man für die drei Basisvektoren durch Gleichsetzung:

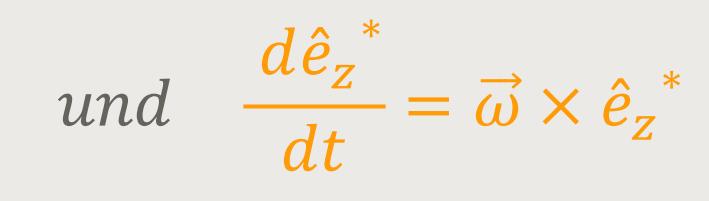
Daraus kann man erkennen, dass in rotierenden Bezugssystemen gleich zwei Trägheitskräfte auftreten.
Um das Verhalten in rotierenden Bezugssystemen näher untersuchen zu können, müssen wir schrittweise vorgehen. Zunächst beschränken wir uns auf gleichförmig rotierende Bezugssysteme.
Im ersten Schritt betrachten wir einen beliebigen Vektor
 , der irgendwo in den
, der irgendwo in den
Hierzu schreibt man sich den Vektor  in Bezug auf beide Systeme
S und S∗ auf. In Bezug auf das
ruhende Inertialsystem ergibt sich:
in Bezug auf beide Systeme
S und S∗ auf. In Bezug auf das
ruhende Inertialsystem ergibt sich:
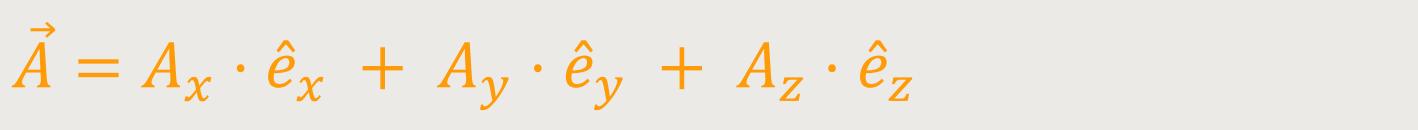
Jetzt kann man den gleichen Vektor  auch
in Bezug auf das rotierende Basisvektorsystem darstellen.
auch
in Bezug auf das rotierende Basisvektorsystem darstellen.
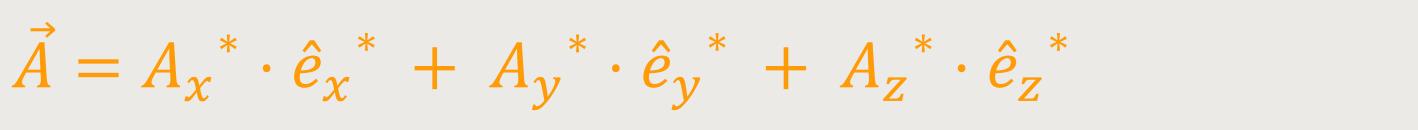
Der Vektor  ist im weiteren Verlauf
nicht konstant. Dieser kann im Laufe der Zeit neben dem Ort auch seine Länge
ändern. Und auch alle anderen Komponenten können sich zeitlich relativ zum
Inertialsystem ändern.
ist im weiteren Verlauf
nicht konstant. Dieser kann im Laufe der Zeit neben dem Ort auch seine Länge
ändern. Und auch alle anderen Komponenten können sich zeitlich relativ zum
Inertialsystem ändern.
Im zweiten Schritt betrachten wir die Änderungen von dem Vektor relativ zu S und relativ zu S∗. Im Anschluss muss man die Beziehungen wieder differenzieren.
Die Änderung des Vektors  nach der Zeit relativ zum ruhenden System
S stellt sich wie folgt dar:
nach der Zeit relativ zum ruhenden System
S stellt sich wie folgt dar:
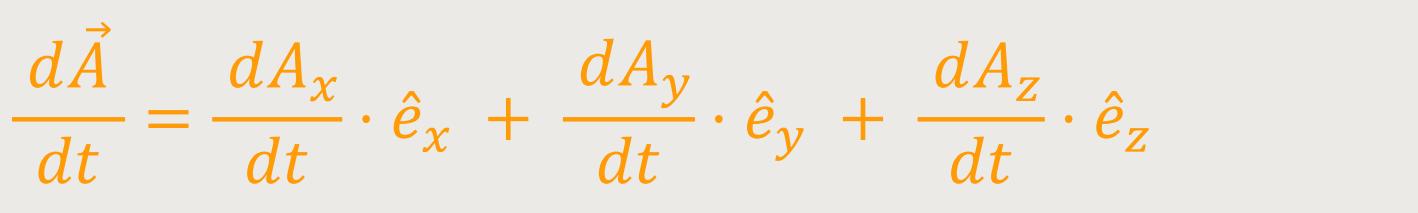
Analog dazu stellt sich die Änderung des Vektors
 nach der Zeit relativ zum
rotierenden System S∗ ähnlich dar:
nach der Zeit relativ zum
rotierenden System S∗ ähnlich dar:
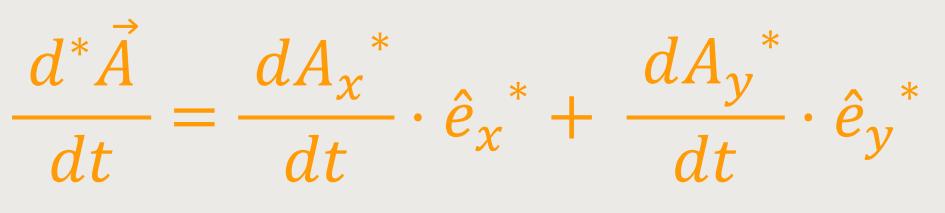
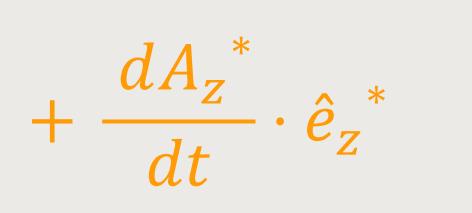
Wie gewohnt muss man auch hier die zeitlichen Änderungen des Vektors wieder
umformen. Dabei geht man so vor, dass man letzten Endes den Zusammenhang zwischen dem
 /dt
/dt /dt
/dt
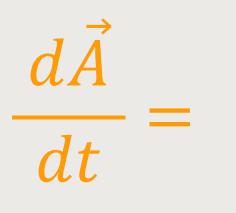
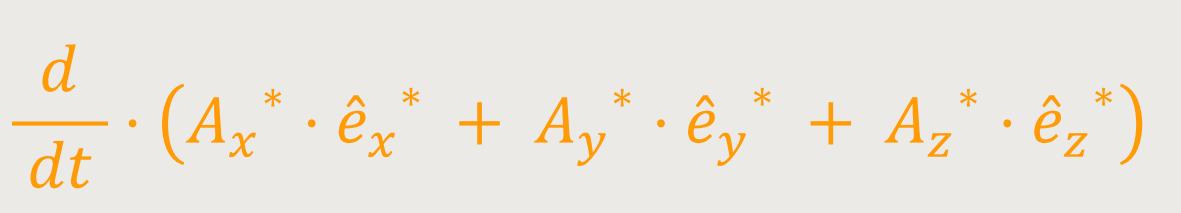
Jetzt formt man weiter nach der Produktregel um, indem man von den Produkten zunächst den ersten Faktor nach der Zeit differenziert, und der zweite Faktor unverändert bleibt. Und anschließend analog dann von den Produkten den ersten Faktor unverändert lässt, und den zweiten Faktor differenziert:
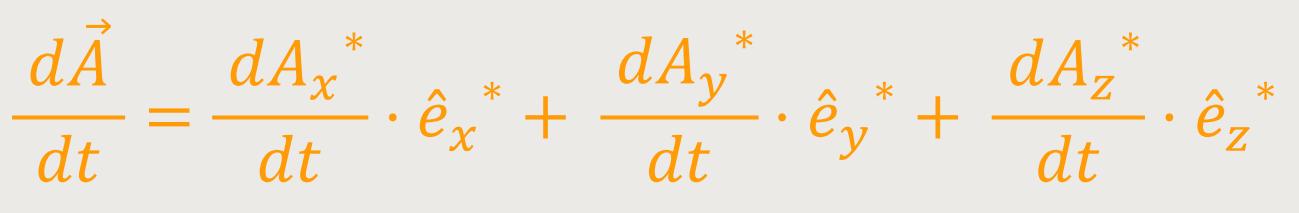
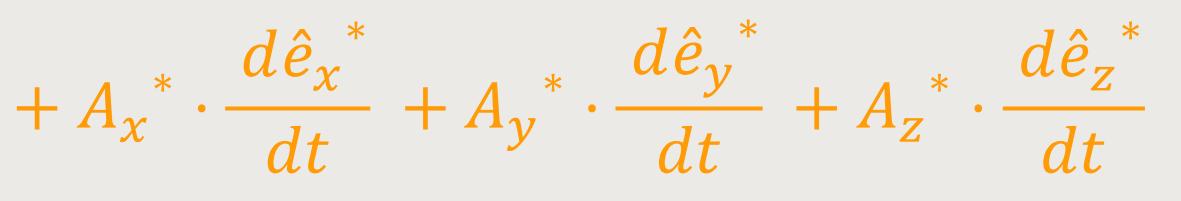
Was ergibt sich daraus? Weiter oben haben wir ja bereits die drei Basisvektoren festgelegt.

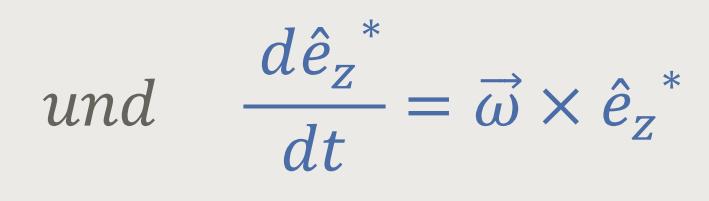
Wenn wir das jetzt entsprechend einsetzten, ergibt sich alternativ für die zweite Differenzierung:


Als Folgerung erhält man:
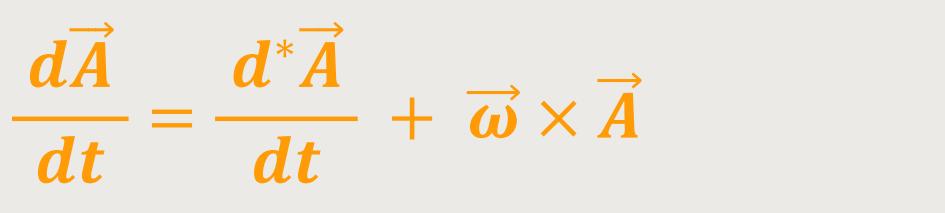
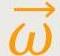 ist wieder die
Winkelgeschwindigkeit des rotierenden Systems relativ zum Inertialsystem.
ist wieder die
Winkelgeschwindigkeit des rotierenden Systems relativ zum Inertialsystem.
Was fängt man jetzt mit dieser einfachen übersichtlichen Formel an?
Nun lässt sich die Geschwindigkeit eines Massenpunktes berechnen, der entweder aus Sicht des ruhenden Systems S oder aus Sicht des rotierenden Systems S∗ betrachtet wird.
Zunächst muss man den Vektor  als Ortsvektor festlegen:
als Ortsvektor festlegen:
 =
=

Es geht dabei um den Ortsvektor des Massenpunktes, dessen Geschwindigkeit wir
ausrechnen wollen. Der Ortsvektor  ist in beiden Systemen immer der gleiche, egal ob man sich das im System S
oder im System S∗ betrachtet. Denn es handelt sich um
ein und denselben Ursprung, der beiden Fällen auf der Rotationsachse liegt. Unter
diesem Vektor versteht man nicht seine zeitliche Veränderung.
ist in beiden Systemen immer der gleiche, egal ob man sich das im System S
oder im System S∗ betrachtet. Denn es handelt sich um
ein und denselben Ursprung, der beiden Fällen auf der Rotationsachse liegt. Unter
diesem Vektor versteht man nicht seine zeitliche Veränderung.
Also, es geht darum, dass man einen Massenpunkt im Raum betrachtet, wobei der Ursprung konstant ist. In diesem Fall ist der Ortsvektor zu diesem Massenpunkt vorgegeben. Nun hat man aber auch zwei Bezugssysteme. Das eine ist das ruhende Inertialsystem S, und das andere ist das rotierende System S∗. Beide Systeme haben denselben Ursprung, und deshalb handelt es sich jeweils um den gleichen Ortsvektor. Aber aus der Sicht des einen wie des anderen Bezugssystems, wird sich dieser Ortsvektor mit der Zeit unterschiedlich ändern.
Dennoch ist er immer der gleiche Ortsvektor und zeigt zu demselben Massenpunkt. Wenn sich der Massenpunkt selbst zusätzlich noch bewegt, also relativ zu dem Inertialsystem, dann ist natürlich auch der Ortsvektor zeitabhängig. Und das trifft dann auf beide Bezugssysteme zu.
Halten wir fest: Der Ortsvektor eines Massenpunktes ist in beiden Systemen jeweils gleich, weil es sich nur um ein und denselben Massenpunkt handelt, und weil die beiden Bezugssysteme immer einen gemeinsamen Ursprung haben. Zudem führen die Bezugssysteme keine Translationsbewegungen durch.
Alles in allem ist jetzt dieser Vektor  der Ortsvektor. Damit erhält man durch Einsetzen:
der Ortsvektor. Damit erhält man durch Einsetzen:
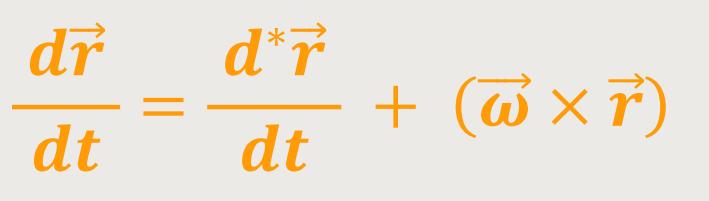
 /dt
/dt
Oder anders ausgedrückt:
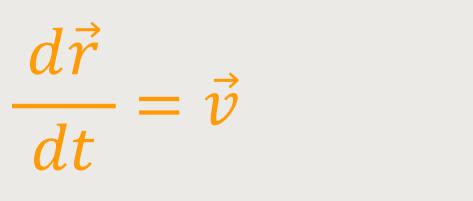
 /dt
/dt
Oder anders ausgedrückt:
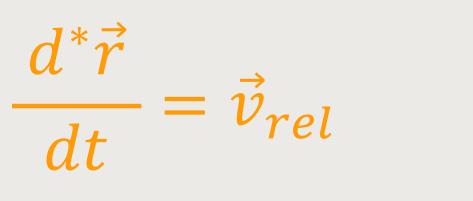
Auch hier kann man den Zusammenhang beider Bezugssysteme gut erkennen:

Was hat das letztlich für eine Bedeutung?
Um das zu erkennen, wollen wir zwei einfache Spezialfälle einfließen lassen.
Falls der Massenpunkt, um den es geht, in S∗ ruht, dann bedeutet das, dass er sich mit dem rotierenden System mitbewegt. So wie wir als Körper oder Massenpunkt auf der Erde. Daraus ergibt sich:
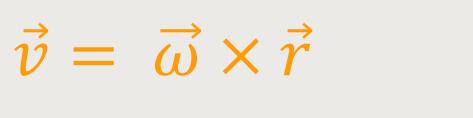
Diese Beziehung kennen wir bereits aus der Kreisbewegung. Die Geschwindigkeit eines
Körpers, der sich auf einer Kreisbahn bewegt, wird dargestellt als
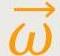 ×
×
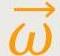 die Winkelgeschwindigkeit dieser
Bewegung ist und
die Winkelgeschwindigkeit dieser
Bewegung ist und  der Ortsvektor
dieses Massenpunktes.
der Ortsvektor
dieses Massenpunktes.
Bezogen auf unsere jetzige Betrachtung heißt das:
Wenn der Körper relativ zu S∗ ruht, aber
S∗ zugleich rotiert und daher der Massenpunkt
mitrotiert, dann beschreibt er eine Kreisbahn und zwar mit der Winkelgeschwindigkeit
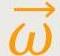 . Seine Geschwindigkeit
. Seine Geschwindigkeit
 ist dann relativ zum ruhenden
Inertialsystem und entspricht
ist dann relativ zum ruhenden
Inertialsystem und entspricht
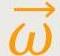 ×
×
Falls der Massenpunkt, um den es geht, jedoch in S ruht, dann bedeutet das, dass er im ruhenden Inertialsystem keine Bewegung vollzieht. Diesmal bewegt sich das rotierende System. Wie sieht dann das rotierende System diesen Massenpunkt? Daraus ergibt sich:
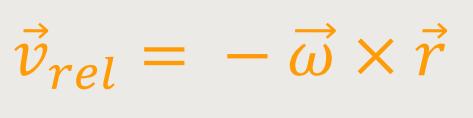
Was ist denn nun der Unterschied zwischen dem Begriff der Geschwindigkeit und der Relativgeschwindigkeit?
Geschwindigkeit ist die Geschwindigkeit des betrachteten Massenpunktes relativ zum ruhenden Inertialsystem. Wobei die Relativgeschwindigkeit die Geschwindigkeit desselben betrachteten Massenpunktes ist, aus Sicht des rotierenden Bezugssystems.
Nachdem wir den Ortsvektor festgelegt haben, berechnen wir jetzt die Beschleunigung.
Hierzu legt man nochmals obige Beziehung zugrunde:
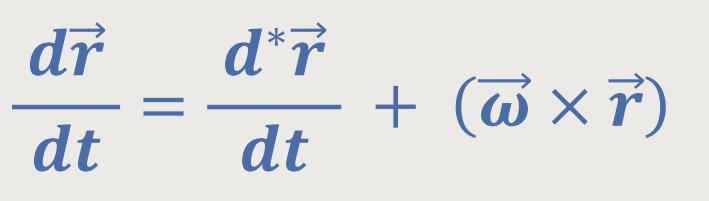
Jetzt geht man allerdings so vor, dass der Vektor
 die Geschwindigkeit
die Geschwindigkeit
 des Massenpunktes relativ zum
ruhenden System ist:
des Massenpunktes relativ zum
ruhenden System ist:

Wenn man das in unsere Beziehung einsetzt, erhält man durch mehrmaliges Umformen:
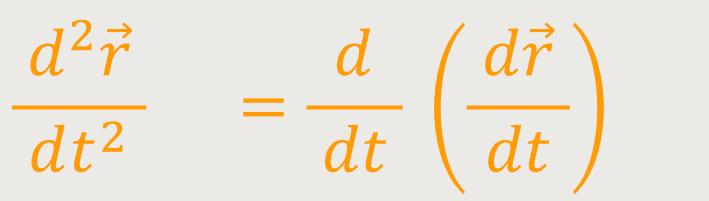
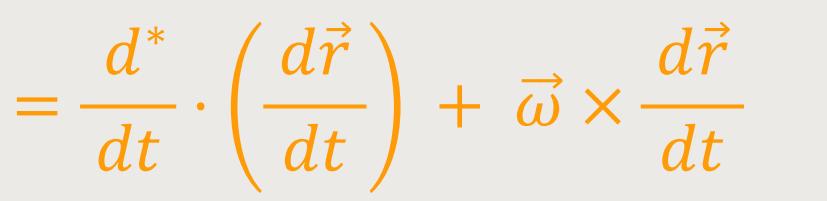
Hinweis: In dieser Formel ist
 /dt =
/dt = 
 auf das Bezugssystem
S bezieht.
auf das Bezugssystem
S bezieht.
Jetzt werden wir schrittweise auf die Größen übergehen, die sich auf das System S∗ beziehen.
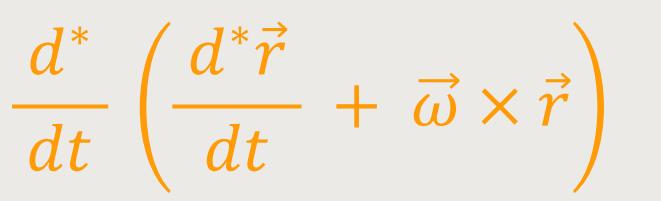
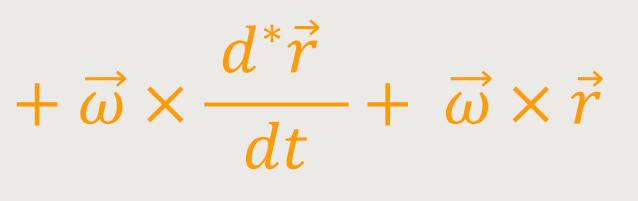
Hinweis: In dieser Formel ist ebenfalls
 /dt +
/dt + 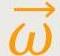 ×
× =
=

 hier auf das
Bezugssystem S∗ bezieht.
hier auf das
Bezugssystem S∗ bezieht.
Jetzt kommt man nicht drumherum, obige Formel zu differenzieren:
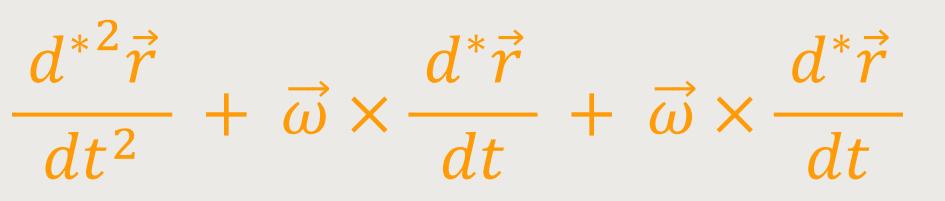
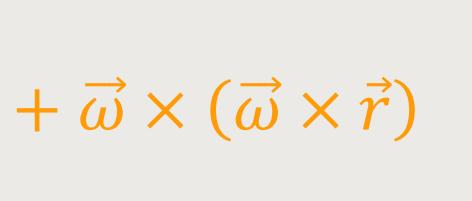
Als Ergebnis erhält man die Beschleunigung des betrachteten Massenpunktes relativ zum ruhenden System:
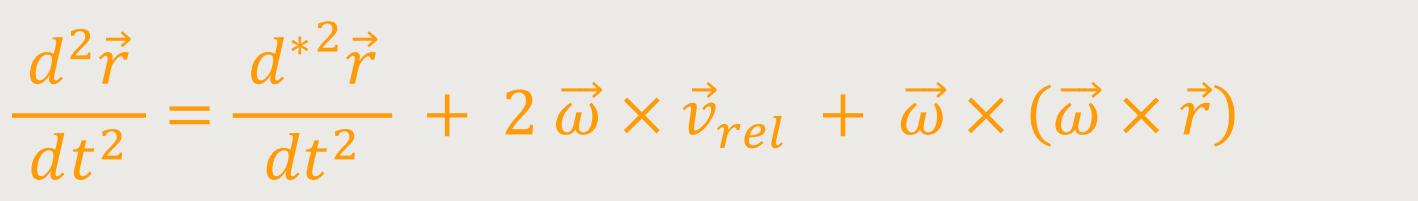
Jetzt kann man die Gleichung leicht umstellen:
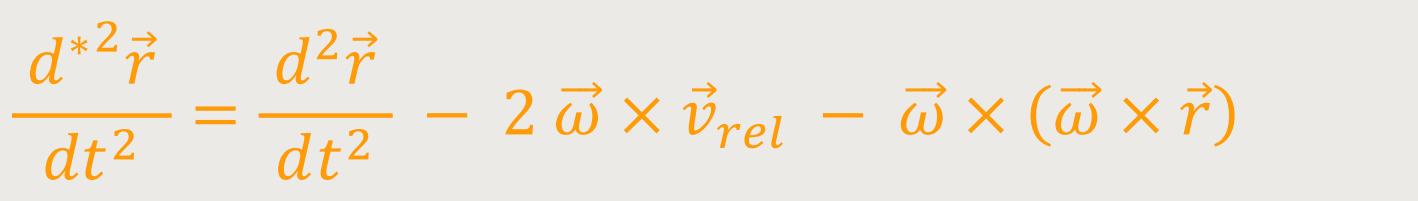
Abschließend braucht man wieder nur die physikalische Interpretation durchführen.
Hierzu nimmt man zunächst an, dass der Massenpunkt unbeschleunigt relativ zum ruhenden System S ist. In diesem Fall wirken natürlich keine eingeprägten Kräfte. Denn eingeprägte Kräfte bewirken immer, dass ein Körper relativ zu einem Inertialsystem beschleunigt ist.
Für das ruhende unbeschleunigte Inertialsystem gilt demnach:
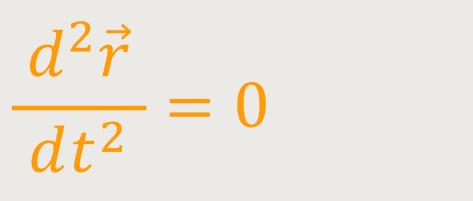
Für das rotierende beschleunigte Bezugssystem gilt anderseits:
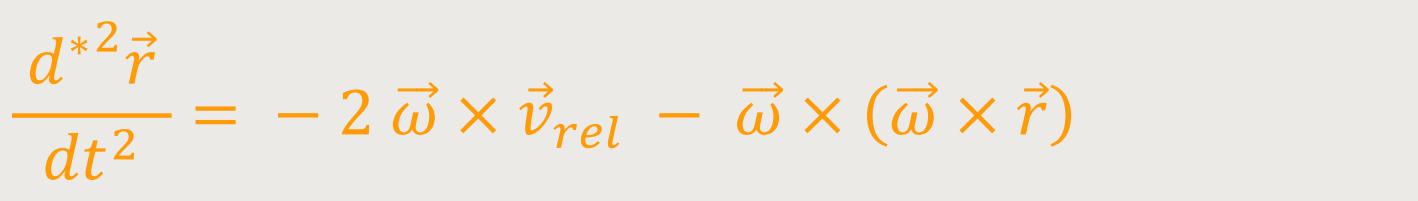
Das bedeutet, der Beobachter im rotierenden System S∗
beobachtet jetzt, dass es eine Beschleunigung gibt, und macht dafür
Trägheitskräfte verantwortlich. Und zwar einerseits eine
sogenannte „Corioliskraft”. Das ist einfach
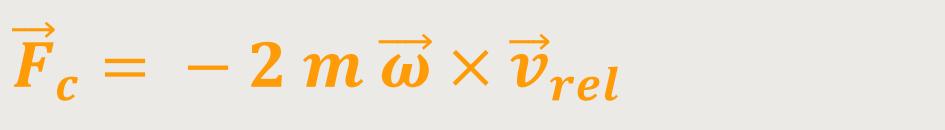
Und andererseits macht der Beobachter eine „Zentrifugalkraft” dafür verantwortlich:
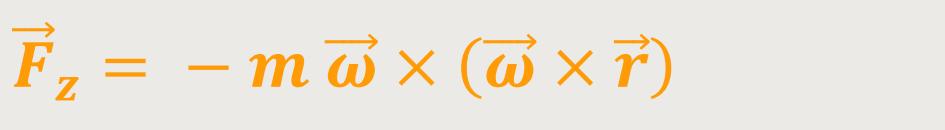
Wenn man sich das nochmals gedanklich vorstellt:
Es geht darum, dass der Massenpunkt als unbeschleunigt in S
angesehen wird, das heißt, es werden keine eingeprägten Kräfte wirken.
Somit nimmt ein Beobachter zwei Arten von Kräften wahr. Die eine ist die
Zentrifugalkraft, die radial nach außen weist. Während die
Corioliskraft nur dann auftritt, wenn sich der betrachtete Körper
zusätzlich noch relativ zu dem rotierenden System bewegt. Und dann steht diese
Kraft senkrecht auf die Relativbewegung, weil wir ja ein vektorielles Produkt
relativ zueinander betrachten.
Der wesentliche Unterschied zwischen der Corioliskraft und der Zentrifugalkraft liegt also darin, dass die Zentrifugalkraft stets auftritt und radial nach außen gerichtet ist, wogegen die Corioliskraft nur dann auftritt, wenn sich der betrachtete Körper noch relativ zu dem rotierenden System bewegt. Die Corioliskraft lenkt die Bewegung seitlich ab.
Jetzt geht man davon aus, dass der Massenpunkt unbeschleunigt oder ruhend ist, relativ zum rotierenden System S∗. Der Massenpunkt rotiert also im Wesentlichen mit diesem System mit. Das stellt sich wie folgt dar:
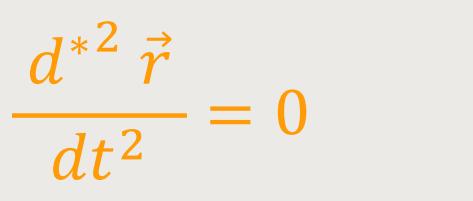
Es gibt also keine Beschleunigung relativ zum rotierenden System und damit erhalten wir:
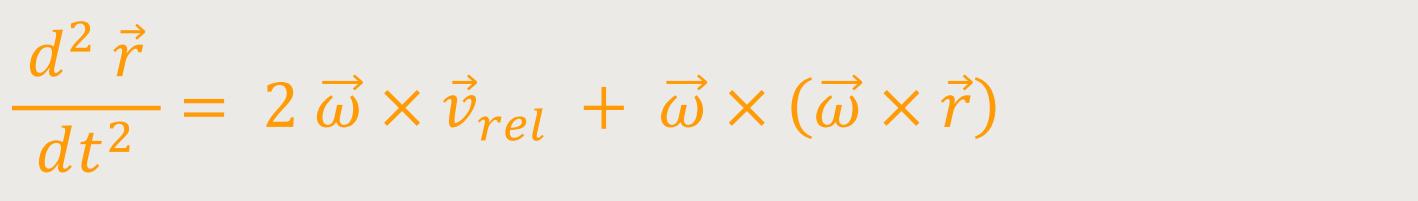
Es ist im Grunde so, als ob ein Beobachter in S∗ keine Gesamtkraft beobachtet, weil aus seiner Sicht die Beschleunigung dieses Körpers gleich Null ist. Es ist also notwendig, dass zusätzliche Kräfte angewendet werden müssen, um diesen Massenpunkt unbeschleunigt relativ zum System S∗ zu halten, nämlich weitere „Führungskräfte”. In diesem Fall ergeben sich zwei Führungskräfte.
Die eine Führungskraft wird definiert als:

Mit dieser Führungskraft wird die Corioliskraft in dem System kompensiert.
Andererseits ergibt sich daraus noch eine zweite Führungskraft:
Diese zweite Führungskraft, die hier auch erforderlich ist, nennt man die „Zentripetalkraft”. Sie ist der Zentrifugalkraft entgegengerichtet. Würde sich zum Beispiel die Erde schneller drehen, würden wir beim Gehen seitlich wegdriften.
Zusammenfassend kann man sagen, die Trägheitskräfte treten nur in
beschleunigten Bezugssystemen auf bzw. speziell in rotierenden Bezugssystemen.
Die eingeprägten Kräfte treten dagegen sowohl in beschleunigten Systemen als
auch in unbeschleunigten Inertialsystemen auf.
Daher ist der entscheidende Unterschied: Eine Trägheitskraft kann
generell durch Übergang auf ein Inertialsystem zum „Verschwinden”
gebracht werden. Eine eingeprägte Kraft hingegen ist gleichermaßen wirksam,
egal ob man sich in einem Inertialsystem oder in einem beschleunigten bzw.
rotierenden Bezugssystem befindet.
Die Zentrifugalkraft betrifft uns auf der Erde relativ wenig. Aber wenn man sich von der Erde weiter weg bewegt, dann wird die Gravitationskraft geringer und die Zentrifugalkraft größer. Schließlich erreicht man eine Position, an der sich beide Kräfte kompensieren. Und deshalb werden auf dieser Umlaufbahn die geostationären Satelliten positioniert.
Insofern ist der Anwendungsfall der geostationären Satelliten nicht uninteressant. Der Bahnradius der Satelliten im Verhältnis zum Erdradius hat nämlich ein ganz besonderes Verhältnis: Dieses Verhältnis beträgt etwa:
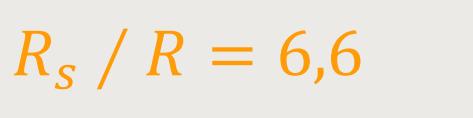
Damit Satelliten wirklich stationär sind, müssen sie in der Äquatorebene der Erde kreisen. Und während sich die Erde dreht, drehen sich die Satelliten mit, sodass sie aus unserer Sicht immer an derselben Stelle stehen.
⇦ Kapitel Kapitel ⇨