Newton lehrte am Trinity College in Cambridge. 1687 veröffent­lichte er ein Buch, das ein Meilen­stein in der Geschichte der Natur­wissen­schaften werden sollte. Heute ist es einfach nur unter dem Namen Principia bekannt. In ihm trug Newton in der ganzen Welt gemachte Beobach­tungen zusammen, und beschrieb sie mathematisch.

Einige Erkenntnisse ragen besonders heraus. So sammelte er zum Beispiel weltweit Daten über einen Kometen, der im Herbst 1680 häufig gesichtet wurde. Auf diese Weise wollte er die Bahn des Kometen bestimmen. Newtons bahn­brechende Entdeckung war, dass die Kraft, die den Kometen um die Sonne schleuderte, dieselbe Kraft war, die Kanonen­kugeln auf die Erde zurück­fallen ließ. Damit gab es einen Nachweis für die Kraft hinter Galileos Fall­gesetzen. Es scheint so, als wenn die gleiche Kraft sogar die Planeten in ihren Umlauf­bahnen hält. Dieser These werden wir in einem gesonderten Kapitel weiter auf den Grund gehen. Zunächst einmal nannte Newton diese Kraft Gravitation und beschrieb sie in einer über­raschend einfachen Gleichung. Diese Gleichung versucht zu erklären, wie sich zwei Massen gegenseitig anziehen, egal ob hier auf der Erde, oder im Weltall:

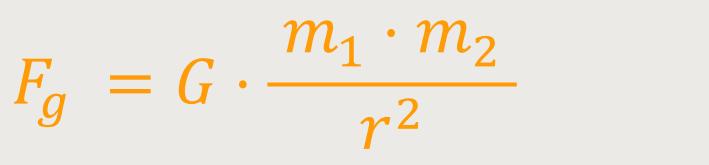
Es ist schon beindruckend, dass dieses und einige andere mathe­matischen Gesetze es ermöglichen, sich im gesamten Universum zu bewegen. Heute können wir diese Kraft sogar jenseits der Milch­straße in Aktion sehen. Wenn zum Beispiel zwei Galaxien voneinander angezogen werden, verschmelzen sie miteinander, und bilden dadurch wiederum neue und größere Galaxien.

Technische Errungenschaften wie das Hubble-Weltraum­teleskop, haben es uns ermöglicht, sogar Sterne ferner Galaxien zu betrachten. So erhielt man jüngst, durch die Beobachtung ferner Gaswolken planetarischer Nebel, Einblicke in die Nukleo­synthese der Elemente.

Was ein Blick in das Weltall auf jeden Fall zeigt ist, dass überall im sicht­baren Universum, und darüber hinaus die gleichen Natur­gesetze gelten. Bisher hat man alle Phäno­mene mit dem Gesetz der Schwerkraft erklärt. Newton schrieb sein Gravitations­gesetz und seine Bewegungs­gesetze basierend auf dem, was hier auf der Erde passiert. Allerdings gibt es eine neue interessante Überlegung, was die Planeten unseres Sonnen­systems auf ihren Bahnen hält. Es handelt sich hierbei um Potential­felder (siehe Kapitel Wirbel­strukturen). Alles an den Galaxien, wie sie sich bilden, und wie sich bewegen, wird durch dieselben mathe­matischen Gesetze beschrieben.

Einige der bedeutendsten Geistes­größen der Welt waren fasziniert davon, wie durch­drungen das Universum von Mathematik ist. Albert Einstein soll sich einmal gefragt haben, „wie kann es sein, das Mathematik unser sichtbares Universum so gut beschreiben kann?” Es schien doch so, als wenn die Mathematik lediglich ein Produkt menschlichen Denkens ist.

Der Nobelpreisträger Eugene Wigner prägte das Wort von der „unplausiblen Effektivität” der Mathematik. Er sagte, „die Tatsache, dass die Mathematik das Universum wirklich so gut beschreiben kann, insbesondere die physikalischen Gesetze, ist ein Geschenk, dass wir weder verstehen noch verdienen.” So sind es insbesondere die Irrationalen Zahlen, die in unserem Kosmos die heraus­ragenden Natur­konstanten bilden.

In der Physik gibt es unzählige Beispiele für diese unplausible Effektivität. Als vor fast 200 Jahren der Planet Uranus von seiner Umlaufbahn abwich, vertrauten die Wissen­schaftler der Mathe­matik. Sie errechneten, dass er vermutlich von einem anderen nicht sichtbaren Planeten angezogen würde. Und so wurde Neptun entdeckt. Wieder war es die Mathematik, die einen bis dahin unbekannten Planeten exakt vorhergesagt hatte.

Viele der heutigen Konsum­gegen­stände sowie unsere Mobilität verdanken wir der Mathematik. Das Fernsehen, der Funk, die Mobil­telefone, die Satelliten oder das GPS. Sie alle kommuni­zieren mittels unsichtbarer Energie­wellen. Bevor James Maxwell ein schottischer Physiker, sich mit ihnen beschäftigte, wusste niemand von ihrer Existenz.

In den 1860er Jahren veröffent­lichte er eine Reihe von Gleichungen, die beschrieben, wie Elektrizität und Magnetismus miteinander verknüpft sind und wie sie sich wechsel­seitig erzeugen können. Die Gleichungen sagten sogar etwas Erstaunliches voraus. Zusammen können Elektrizität und Magnetismus die Energiewellen erzeugen, die sich mit Licht­geschwindigkeit durch den leeren Raum bewegen. Wir kennen diese auch unter dem Begriff „Elektro­magnetische Wellen”. Ihrer Entdeckung verdanken wir die Unterhaltungs­industrie und viele Apparaturen in der Medizin.

Die Menschen machten sich daran, diese Wellen zu finden, die Maxwells Gleichungen progno­stiziert hatten. So entdeckte Guglielmo Marconi schließlich die Radio­wellen. Er fand heraus, dass die elektrische Entladung kurzzeitig ein magne­tisches Feld erzeugt, das seiner­seits kurzzeitig ein elektrisches Feld erzeugt, welches wiederum kurz­zeitig ein magne­tisches Feld erzeugt usw. durch den kreisenden Energie­fluss zwischen den beiden breitet sich eine elektro­magnetische Welle aus. So war es im Laufe der Zeit möglich, Funksignale schließlich bis über den Atlantik zu schicken. Derartige Funk­signale, damals in Form des Morse-Codes, retteten zahlreichen Menschen auf der Titanic das Leben. Das Zeitalter der drahtlosen Kommunikation hatte begonnen.

Seit Maxwell und Marconi haben die Beweise für die Vorhersage­kraft der Mathematik weiter zugenommen. Vor allem trifft das auf die Welt der Physik zu. Vor etwas mehr als 100 Jahren wussten die Menschen kaum etwas über die Existenz der Atome. Ja, es gab Vermutungen und die unter­schied­lichsten Theorien. Aber erst durch Experimente konnten ihre Bestand­teile verifiziert werden. So entdeckte man das Elektron, das Proton und das Neutron. Als Physiker tiefer eintauchen wollten, half die Mathematik dabei, die Weichen richtig zu stellen. Schließlich entdeckte man eine ganze Armada von Elementar­teilchen. Und wir haben das Ende der Fahnen­stange noch nicht erreicht. Folgendes Zitat aus einem Bestseller bringt das treffend zum Ausdruck: „Alles hat er schön gemacht zur passenden Zeit. Er hat ihnen sogar die Ewigkeit ins Herz gelegt, doch das Werk, das der wahre Gott von Anfang bis Ende vollbracht hat, werden die Menschen nie ergründen” (Prediger 3:11). Diese Entdeckungs­reise hält bis heute an.

Was die Vorhersage­kraft der Mathematik angeht, könnte man folgendes Beispiel anführen: Vor über 50 Jahren wurde die Existenz eines subatomaren Teilchens mathe­matisch vorher­gesagt. Am Cern, in Genf, in der Schweiz befindet sich die europäische Organisation für Kern­forschung. Die Einrichtung ist berühmt für ihren großen Hadronen-Speicherring. Seit Jahrzenten wurde daran gearbeitet, Teilchen mit nahezu Licht­geschwindig­keit auf eine bestimmte Weise aufeinander prallen zu lassen.

Wenn die mathema­tischen Berech­nungen präzise genug wären, würde man ein neues Teilchen entdecken. Man war auf der Suche nach dem sogenannten Higgs-Teilchen. Das Vorhanden­sein eines solchen Teilchens wäre der Beweis für das Higgs-Feld. Dabei handelt es sich quasi um ein Energie­feld, das verschie­denen Elementen Masse verleiht. Weil das Higgs-Teilchen und das gleichnamige Feld ein so fundamentaler Teil der Physik ist, bekam es den Spitznamen „Das Gottes­teilchen”. Im Jahre 2012 bestätigten Experimente am Cern schließlich die Existenz des Higgs-Teilchens.

Einige haben sich gefragt, wie kann die Mathematik so effektiv sein? Die Antwort lautet, sie ist eine natur­gegebene Wahrheit und stammt offen­sichtlich von jemandem, der die Gesetze ins Leben gerufen hat. Wir Menschen sind nicht die Erfinder der Mathematik, sondern lediglich die Entdecker der Zusammen­hänge. Ohne Mathe­matik hätten wir die Naturwissen­schaften im Allgemeinen und die Physik im Speziellen nicht ergründen können.

Mit Hilfe mathematischer Modelle können wir in die Physik eintauchen. Wir entwickeln zum Beispiel Modelle für die Wetter­vorhersage. Wenn­gleich Meteo­rologen das Wetter nur für etwas mehr als eine Woche vorher­sagen können. Überall dort, wo man mit den unterschied­lichsten Wechsel­wirkungen zu tun hat, stoßen mathematische Modelle an ihre Grenzen. Egal, ob es der Aktien­markt ist oder die neuronalen Inter­aktionen in unserem Gehirn. Es lässt sich zwar in groben Zügen eine Wahrschein­lichkeit bzw. Tendenz berechnen, aber der Schlüssel liegt oft im Detail, der uns oftmals verborgen bleibt.

Wer einen technischen Beruf ausübt kann bestätigen, wie einer­seits physikalische Kräfte und ander­seits die Grenzen der Mathematik aufeinander treffen. Jemand hat es mal sehr schön ausgedrückt: „Beim Konstruieren und Bauen von Dingen trifft die Eleganz der Mathematik auf das Chaos der Realität. Aber die Praxis­tauglichkeit hat Vorrang.” Die Mathematik bewegt sich stets im Bereich des Absoluten. Und zahlreiche Natur­konstanten werden durch Zahlen definiert, die unendliche Werte haben. Doch als Ingenieur bzw. Konstrukteur bewegt man sich im Bereich der Annäherung. Man ist vor allem an der Praxis­tauglichkeit interessiert. Aus diesem Grund sind die Berechnungen häufig nur Näherungs­lösungen. Man lässt des Öfteren Gleichungen weg, um die Dinge so einfach wie möglich zu gestalten. Die Konstruk­tionen müssen vor allem zweck­dienlich sein, und den menschlichen Bedürfnissen entsprechen.

Bei vielen der bedeutendsten Ingenieur­leistungen wurde lediglich mit mathe­matischen Abkürzungen gearbeitet. Es reicht im Allgemeinen sogar aus, allenfalls nur bis maximal zur 5. Stelle hinter dem Komma zu rechnen.

Die Mathematik kann viele Geheim­nisse des Universums auf geheimnis­volle Art und Weise enthüllen. Und nur weil wir mit der Präzision der Mathematik noch nicht umgehen können, reduzieren wir sie manchmal auf ein unvoll­kommenes Werkz­eug, als ob wir sie selbst erfunden hätten.

Vielleicht denken wir so, weil wir alle Dinge, die wir sehen, abstrahieren. Wir sehen, dass unser Gegenüber zwei Augen, zwei Ohren, zwei Hände hat. Demnach ist die Zahl „Zwei” ein erfundener Begriff. Wir entdeckten auch, wie sich Zahlen­mengen zu einander verhalten. Bei der Frage, wie viele Finger habe ich, sagen wir „Fünf” oder „Zehn”, je nachdem wie viele Hände wir betrachten. Aber dabei übers­ehen wir, dass sich selbst die Finger an einer Hand nicht gleichen. Jeder Finger ist einzigartig, so wie jede chemische Verbindung im Universum. Es gibt kein gleich, es gibt allenfalls nur ähnlich. Die scheinbare Inhomo­genität lehren uns die Natur­konstanten. Und dennoch sehen wir eine Präzision, wie ein Schweizer Uhrwerk. Menschen haben die komplexen Beziehungen entdeckt, die verschiedene Zahlen unter­einander haben. Doch kann man wirklich sagen, dass wir das Konzept erfunden haben? Was ist, wenn der Mensch nur ein winzig kleiner Teil eines erhabenen Ganzen ist?

Was ist, wenn die Natur­konstanten in Wirklich­keit in unseren Genen verankert sind, und wir deshalb ein Verständnis für Mathematik entwickeln können? Wir mögen vielleicht eine gewisse Vorstellung davon haben, wie das alles funktioniert, aber die komplette Antwort wird uns immer verborgen bleiben. Letzt­endlich bleibt es das große Geheimnis der Mathematik oder besser gesagt, das Geheimnis der Schöpfung.

Was ist Mathematik also? Ein entdeckter Teil des Universums oder eine eher irdische Erfindung? Mir gefällt der Gedanke, dass Mathematik im Grunde die Lebens­energie ist, die etwas Abstraktem wie der Physik oder der Chemie eine Bewegungs­freiheit verschafft, mit der wir im Laufe der Zeit sogar sehr komplexe Frage­stellungen lösen können. Vielleicht werden wir uns eines Tages genauso selbst­verständlich im All bewegen, wie wir heute mit dem Smartphone umgehen.

Nur weil wir gegenwärtig nicht alle chemischen, mathema­tischen und physika­lischen Zusammen­hänge verstehen, heißt es noch lange nicht, dass etwas unmöglich ist. Angefangen bei der Frage nach dem Sinn des Lebens, oder warum wir alt werden und sterben. Vielleicht kommen wir der Antwort näher, wenn wir uns eingestehen, dass unser Universum einen Anfang hatte, doch vermutlich nicht so, wie wir es uns gegenwärtig vorstellen.

Gehen wir nun noch kurz auf einige ungelöste physikalische Phänomene ein.

⇦ Kapitel Kapitel ⇨