Abb. 1: Albert Einstein
(Ferdinand Schmutzer – gemeinfrei)

Der Titel dieser Abhandlung stammt von keinem geringeren als Albert Einstein. Er hatte sich bereits 1911 mit der Frage beschäftigt, ob es eine „variable” Licht­geschwindig­keit gibt. Am 10. Oktober 1911 schrieb er an seinen ehemaligen Mitarbeiter Laub: „... Ich halte es für wahr­scheinlich, dass das Prinzip von der Konstanz der Licht­geschwindig­keit in seiner gewohnten Fassung nur für Räume konstanten Gravitations­potentials gilt.”

Bereits damals gelangte Einstein zu der Annahme, dass ein Licht­strahl im Schwere­feld gekrümmt sein müsse. Leider haben sich nur wenige Wissen­schaftler mit dieser Über­legung nach­haltig beschäftigt. Für sie wider­spräche es der Allgemeinen Relativitäts­theorie, obwohl ironischer Weise beide Formulierungen von Albert Einstein selbst angestoßen wurden. Erstere hätte ebenfalls revolutionäre Konsequenzen haben können.

Besonders bekannt sind die Spezielle und die Allgemeine Relativitäts­theorie, die er 1905 bzw. 1915 endgültig formu­lierte. Doch was nur wenigen bewusst ist, Einstein hatte zwar seine Spezielle Relativitäts­theorie auf der Grund­lage einer konstanten Licht­geschwindig­keit hergeleitet, grübelte aber bald danach über einer allgemein­gültigen Formulierung. Denn was für Bewegungen nahe der Licht­geschwindig­keit gilt, konnte auch für Gravitations­felder gelten. Einsteins Ansatz hätte es prinzipiell ermöglicht, eine fundamentale Natur­konstante, nämlich Newtons Gravitations­konstante, zu berechnen und damit über­flüssig zu machen.

Die Frage, ob die Ausbreitung des Lichts durch die Schwere beeinflusst wird, hatte Einstein bereits 3 Jahre zuvor im Jahre 1908 in einer Abhand­lung zu beantworten versucht. Aber nach seinen Worten haben ihn seine ersten Über­legungen nicht befriedigt. Außerdem wäre man inzwischen in der Lage durch Experimente seine Theorie zu über­prüfen. Im gleichen Jahr hatte er sogar das „Äquivalenz­prinzip” formuliert, bei der die schwere und die träge Masse eines Körpers zwei äquivalente Größen sind.

Einstein erkannte, dass es unmög­lich war zu unter­scheiden, ob man im schwere­losen Weltraum von einer beschleuni­genden Kraft angetrieben wird oder ob diese Kraft von einem gewöhn­lichen Gravitations­feld herrührt. Deshalb folgerte Einstein, dass auch Licht­strahlen in einem Gravitations­feld eine „Krümmung” erfahren mussten. Diese Vorher­sage der Allgemeinen Relativitäts­theorie, wurde inzwischen durch zahl­reiche Unter­suchungen bestätigt. Heute spricht man zwar lieber von einer „geraden” Licht­ausbreitung in einem gekrümmten Raum, aber beides ist mathe­matisch äquivalent. Beschäftigen wir uns nun etwas näher mit seiner revolu­tionären Idee.

Einsteins Auffassung nach müsste man beobachten können, dass Licht­strahlen, die in der Nähe der Sonne vorbei­gehen, durch das Gravitations­feld der Sonne eine Ablenkung erfahren würden, so dass eine schein­bare Vergrößerung des Winkel­abstandes eines nahe an der Sonne erscheinenden Fixsternes von fast „einer” Bogen­sekunde zu beobachten sein müsste.

In seinen Über­legungen war Einstein auch auf weitere Aspekte der Gravitation gestoßen. Wegen der Komplexi­tät des Sach­verhalts konnte sich Einstein in der nach­folgenden Abhandlung aber nur auf das Wesentliche beziehen. Dennoch würde es dem Betrachter die Möglich­keit geben, selbst Rück­schlüsse zu ziehen. Einstein war sich zum damaligen Zeit­punkt bewusst, dass die abgeleiteten Beziehungen selbst bei Bestätigung durch Astronomen nur in erster Näherung gültig wären.

Zunächst fragte sich Einstein, wie ein Gravitations­feld beschaf­fen sein müsste, um seiner Theorie zu genügen. Er betrachtete in Gedanken zwei Koordinaten­systeme, von dem sich eines in einem Schwere­feld befindet, wogegen das andere „ohne” Schwere­feld wäre.

In einem homogenen Schwere­feld mit einer Schwere­beschleunigung γ befände sich zudem ein ruhendes Koordinaten­system K, welches so orientiert sei, dass die Kraft­linien des Schwere­feldes in Richtung der negativen z-Achse verlaufen. In einem von Gravitations­feldern freien Raum befände sich ein zweites Koordinaten­system K', das in Richtung seiner positiven z-Achse eine gleich­förmig beschleunigte Bewegung mit einer Beschleunigung γ ausführe. Grund­lage für die weitere Betrach­tung sollten die Gesetze der Kinematik und der Mechanik bilden.

Nun sollten sich relativ zum System K und relativ zum System K' punktförmige Massen bewegen, die keinen Gravita­tions­wechsel­wirkungen ausgesetzt seien. Dann würden sich für die Beschleu­nigung folgende Gleichungen ergeben:

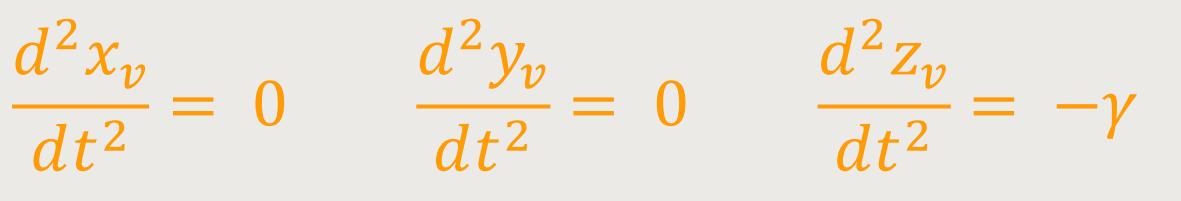
Diese Beziehungen lassen sich für das beschleu­nigte System K' direkt aus dem Galileischen Prinzip ableiten. Dagegen ergibt sich für das in einem homogenen Gravitations­feld ruhende System K aus der Erfahrung, dass in einem solchen Feld alle Körper gleich stark und gleich­mäßig beschleunigt werden. Obwohl uns die Natur lehrt, dass alle Körper im Gravitations­feld gleich schnell fallen und eines der fundamentalsten Gesetze ist, hatte dieses Gesetz das physika­lische Welt­bild zur Zeit Einsteins noch nicht nach­haltig geprägt.

Erkennt man diese Natur­beobachtung jedoch an, gelangt man zu einer sehr befriedigenden Inter­pretation, nämlich, dass die Systeme K und K' physika­lisch genau gleich­wertig sind. Das heißt, man kann davon ausgehen, dass sich das System K letztlich eben­falls in einem von einem Schwere­feld freien Raum befindet. Und man müsste das System K als gleich­förmig beschleunigt betrachten. Einstein gab den Hinweis, dass man bei dieser Gleich­setzung ebenso wenig von der „absoluten Beschleu­nigung” des Bezugs­systems sprechen könne, wie man nach der Allge­meinen Relativitäts­theorie von der „absoluten Geschwindig­keit” eines Systems reden könne.

Einstein war sich bewusst, dass man ein beliebiges Schwere­feld nicht durch einen Bewegungs­zustand des Systems ohne Gravitations­feld ersetzen kann, ebenso wenig, wie man durch eine Relativitäts­trans­formation alle Punkte eines beliebig bewegten Mediums in einen Ruhe­zustand trans­formieren kann.

Man kann also die gleiche Fall­beschleu­nigung in einem Gravitations­feld als selbst­verständ­lich ansehen. Solange man sich auf rein mechanische Vorgänge aus dem Gültig­keits­bereich von Newtons Mechanik beschränkt, kann man sich der Gleich­wertig­keit der Systeme K und K' sicher sein. Die Über­legungen werden nur dann tiefere Bedeu­tung haben, wenn die Systeme K und K' in Bezug auf alle physika­lischen Vorgänge gleich­wertig sind. Das heißt, wenn die Natur­gesetze in Bezug auf das System K mit denen im System K' voll­kommen über­ein­stimmen. Würden wir dies nach Einsteins Worten annehmen, erhalten wir ein Prinzip, das, falls es wirklich zutrifft, eine große heuristische Bedeutung besitzt. Denn man erhält durch die theoretische Betrachtung der Vorgänge, die sich relativ zu einem gleich­förmig beschleu­nigten Bezugs­system abspielen, Aufschluss über den Verlauf der Vorgänge in einem homogenen Gravitations­feld. Einstein gibt den Hinweis, dass dieses hier in Betracht kommende Gravitations­feld nur in erster Annäherung homogen ist.

In den nächsten Absätzen wollte Einstein zunächst zeigen, inwie­fern seine Hypo­these aus Sicht der Allgemeinen Relativitäts­theorie an Wert gewinnt.

Die Relativitäts­theorie hatte ergeben, dass die träge Masse eines Körpers mit dem Energie­inhalt desselben wächst. Beträgt der Energie­zuwachs beispiels­weise E, so ist der Zuwachs an träger Masse gleich E/c², wobei c die Licht­geschwindig­keit bedeutet. Nun stellt sich Frage, ent­spricht diesem Zuwachs an träger Masse auch ein Zuwachs an gravitativer Masse? Wenn das nicht zutrifft, so schluss­folgerte Einstein, fiele ein Körper in demselben Schwere­feld mit verschiedener Beschleunigung je nach dem Energie­inhalt des Körpers. In diesem Fall könnte die Schluss­folgerung der Relativitäts­theorie, nach welcher die Aussage von der Erhaltung der Masse mit der Aussage von der Erhaltung der Energie gleich­bedeutend ist, nicht aufrecht erhalten werden. Denn dann müsste man die Aussage von der Erhaltung der Masse für die „träge” Masse aufgeben, dagegen für die gravitative Masse aufrecht­erhalten.

Einstein betrachtete dies als sehr unwahr­scheinlich. Anderer­seits liefert die Allge­meine Relativitäts­theorie kein Argument, aus dem man schluss­folgern könnte, dass das Gewicht eines Körpers von dessen Energie­inhalt abhängt. Einstein wollte nun zeigen, dass seine Hypothese von der Äquivalenz der Systeme K und K' die Schwere der Energie als notwendige Konsequenz liefert.

Einstein schlägt folgendes Gedankenexperiment vor:

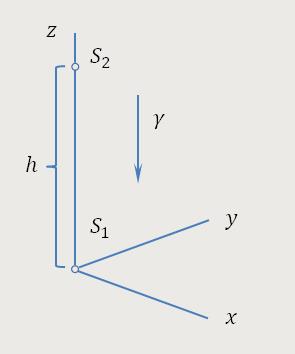
Abb. 2

Es befinden sich zwei mit Mess­instrumenten versehene Körper­systeme S₁ und S₂, in einem Abstand h auf der z-Achse im Koordinaten­system K. Im Verhältnis zum Abstand seien diese beiden Körper­systeme unend­lich klein. Außer­dem sei das Gravitations­potential in S₂ um den Wert γ · h größer, als das im Körper­system S₁. Während also beide Körper­systeme eine Beschleunigung auf der z-Achse erfahren, wird jetzt von S₂ nach S₁ eine bestimmte Energie­menge E in Form von Strahlung ausge­sendet. Die Energie­mengen sollen dann in beiden Körper­systemen mit besagten Mess­instru­menten gemessen werden. Der Mess­vorgang sollte irgendwo auf der z-Achse statt­finden, und die Mess­ergebnisse sollten voll­kommen gleich sein. Laut Einstein lässt über den Vorgang dieser Energie­über­tragung durch Strahlung grund­sätzlich nichts aussagen, weil man den Einfluss des Schwere­feldes auf die Strahlung und die Mess­instrumente in S₁ und S₂ noch nicht kannte.

Da aber zuvor voraus­gesetzt wurde, dass die Koordinaten­systeme K und K' äquiva­lent sind, kann an Stelle des im homo­genen Schwere­feld befind­lichen Koordinaten­systems K das schwere­freie, auf der z-Achse in positive Richtung gleich­förmig beschleunigt bewegte Koordinaten­system K' gesetzt werden. Die Körper­systeme S₁ und S₂ seien auch hier mit der z-Achse des Koordinaten­systems K' fest verbunden.

Den Vorgang der Energie­über­tragung durch Strahlung von S₁ und S₂ wird nun von einem dritten Koordinaten­system K₀ aus beurteilt, wobei dieses Koordinaten­system beschleunigungs­frei sei. In Bezug auf K₀ besitzt K' in dem Augen­blick, in welchem die Strahlungs­energie E₂ von S₂ gegen S₁ abgesendet wird, die Geschwindig­keit Null. Die Strahlung wird in S₁ ankommen, wenn die Zeit h/c verstrichen ist (in erster Annäherung). In diesem Moment besitzt aber S₁ in Bezug auf K₀ die Geschwindig­keit v = γ · h/c. Deshalb besitzt nach der Allgemeinen Relativitäts­theorie die in S₁ ankommende Strahlung nicht die Energie E₂, sondern eine größere Energie E₁, welche mit E₂ in erster Annäherung durch folgende Gleichung verknüpft ist:

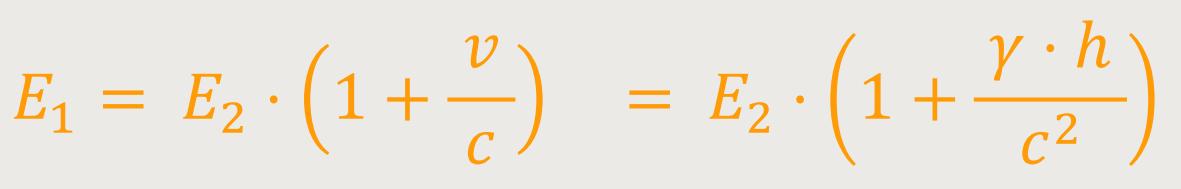
Demnach müsste gemäß obiger Voraus­setzung die gleiche Beziehung, falls derselbe Vorgang in dem nicht beschleu­nigten, aber mit einem Gravitations­feld versehenen System K, statt­findet. In diesem Fall kann γ · h durch das Potential Φ des Gravita­tions­vektors im Körpersystem S₂ ersetzt werden, wenn die willkür­liche Konstante von Φ im Körper­system S₁ gleich Null gesetzt wird. Daraus ergibt sich die Gleichung:

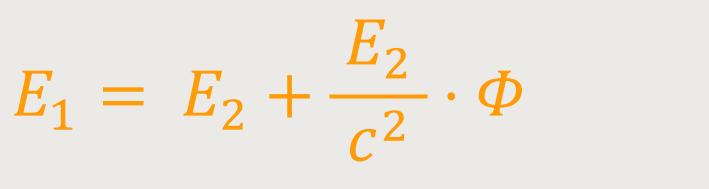
Diese Gleichung ent­spricht laut Einstein dem Energie­satz.

Die in S₁ ankommende Energie E₁ ist größer als die mit dem gleichen Ver­fahren gemessene Energie E₂, die in S₂ emittiert wurde. Und zwar größer um den Wert aus der poten­tiellen Energie der Masse E₂/c² im Schwere­feld. Es zeigt sich also, dass man, um das Energie­prinzip weiterhin zu erfüllen, der Anfangs­energie E vor ihrer Aus­sendung vom Körper­system S₂ eine potentielle Energie der Schwere zuschreiben muss, die der schweren Masse E/c² entspricht. Die Annahme der Äquivalenz von K und K' steigert also die zu Beginn dieses Unter­themas erwähnte Schwierig­keit, welche die Allge­meine Relativitäts­theorie bestehen lässt.

Besonders deutlich zeigt sich der Sinn dieses Ergebnisses bei der Betrach­tung eines Kreis­prozesses. Einstein beschreibt im Nach­folgenden 5 Schritte:

1. Zunächst sendet man die Energie E, die im Körper­system S₂ gemessen wurde, in Form von Strahlung ausgehend von S₂ nach S₁, wo nach dem zuvor Beschrie­benen die Energie E · (1 + γ · h/c²) aufgenommen wird, so wie sie auch in S₁ gemessen wird.


2. Als nächstes senkt man einen Körper W von der Masse M von S₂ nach S₁, wobei die Arbeit M · γ · h nach außen abgegeben wird.


3. Nun überträgt man die Energie E von S₁ auf den Körper W, während sich der Körper W in S₁ befindet. Dadurch ändert sich die schwere Masse M, so dass sie jetzt den Wert M' erhält.


4. Anschließend hebt man den Körper W wieder nach S₂, wobei nun die Arbeit M' · γ · h aufzuwenden ist.


5. Zum Schluss überträgt man die Energie E vom Körper W wieder auf das Körper­system S₂.

Der Effekt dieses Kreis­prozesses besteht einzig und allein darin, dass das Körper­system S₁ einen Energie­zuwachs E · (γ · h/c²) voll­zogen hat, und dass diesem System die Energie­menge ...

... in Form von mechan­ischer Arbeit zugeführt wurde. Nach dem Energie­prinzip ergibt sich also:

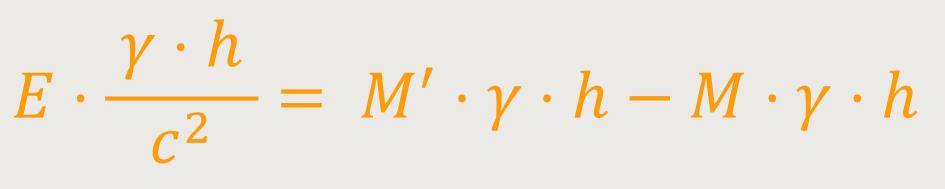
Nach Kürzen erhält man:

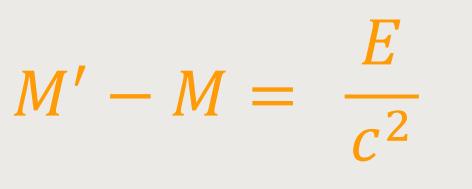
Der Zuwachs an schwerer Masse ist demnach gleich E /c², bzw. es entspricht dem aus der Relativitäts­theorie sich erge­benden Zuwachs an träger Masse.

Noch unmittelbarer ergibt sich das Resultat aus der Äquivalenz der Systeme K und K', nach der die schwere Masse in Bezug auf K der trägen Masse in Bezug auf K' voll­kommen gleich ist. Als Schluss­folgerung muss deshalb die Energie eine „schwere” Masse besitzen, die ihrer trägen Masse gleich ist. Hängt man beispiels­weise im System K' eine Masse M₀ an einer Feder­waage auf, so wird die Waage wegen der Träg­heit von M₀, das schein­bare Gewicht M₀ · γ anzeigen. Über­trägt man die Energie­menge E auf M₀, so wird die Feder­waage nach dem Trägheits­satz (M₀ + E/c²) · γ anzeigen. Nach der eingangs präzisierten Grund­annahme muss dasselbe Ergebnis heraus­kommen, wenn man diesen Versuch im System K, sprich im Gravitations­feld wiederholt.

Einstein entwickelt diesen Gedanken­gang weiter, indem er jetzt die Zeit und Licht­geschwindig­keit auf das Schwere­feld bezieht. Hierzu nimmt er zwei baugleiche Uhren mit einer bestimmten Frequenz in sein Gedanken­experiment mit auf.

Wenn die im gleich­förmig beschleu­nigten Bezugs­system K' in S₂ gegen S₁ emittierte Strahlung mit Bezug auf die in S₂ befindliche Uhr die Frequenz v₂ besaß, so besitzt sie in Bezug auf S₁ bei ihrer Ankunft in S₁ in Bezug auf die in S₁ befindliche gleich beschaffene Uhr nicht mehr die Frequenz v₂ sondern eine größere Frequenz v₁, und zwar in der Form, dass in erster Annäherung gilt (2):

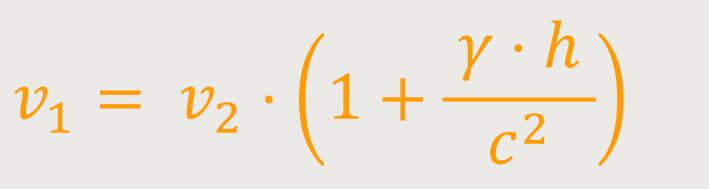
Führt man nämlich wieder das beschleu­nigungs­freie Bezugs­system K₀ ein, relativ zu welchem K' zur Zeit der Licht­aussendung keine Geschwindig­keit besitzt, so hat S₁ in Bezug auf K₀ zur Zeit der Ankunft der Strahlung in S₁ die Geschwindig­keit γ · (h/c), woraus sich die angegebene Beziehung aufgrund des Dopplerschen Prinzips unmittel­bar ergibt.

Nach Einsteins Voraus­setzung von der Äquivalenz der Systeme K und K' gilt diese Gleichung auch für das ruhende, mit einem gleich­förmigen Schwere­feld versehene Koordi­naten­system K, falls in diesem die geschilderte Strahlungs­über­tragung statt­findet. Es ergibt sich also, dass ein bei bestimmtem Schwere­potential in S₂ emittierter Licht­strahl, der bei seiner Emission – mit einer in S₂ befind­lichen Uhr verglichen – die Frequenz v₂ besitzt, bei seiner Ankunft in S₁ eine andere Frequenz v₁ besitzt, falls letztere mittels einer in S₁ befindlichen gleich­artigen Uhr gemessen wird.

Einstein ersetzt jetzt γ · h durch das Schwere­potential Φ von S₂ in Bezug auf S₁ als Null­punkt und setzt voraus, dass die für das homogene Gravitations­feld abgeleitete Beziehung auch für anders gestaltete Felder gilt. Aus dieser Über­legung ergibt sich (2a):

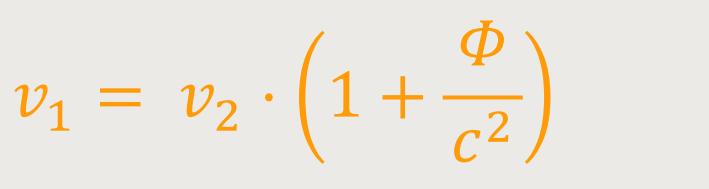
Dieses, nach Einsteins Ableitung in erster Näherung gültige Resultat, lässt sich nach seinen Worten zunächst wie folgt anwenden: Es sei v₀ die Schwingungs­zahl eines elementaren Licht­erzeugers (Licht­quelle), gemessen mit einer an demselben Ort gemessenen Uhr U. Diese Schwingungs­zahl ist dann unabhängig davon, wo der Licht­erzeuger samt der Uhr auf­gestellt wird. Man könnte sich beide z.B. in der Nähe der Sonnen­oberfläche denken (dort befände sich das System S₂). Von dem dort emittierten Licht gelangt ein Teil zur Erde (S₁), wo sich mit einer Uhr U von gleicher Bauart, wie die zuvor beschriebene, die Frequenz v des ankommenden Lichts messen lässt. Dann ergibt sich aus vorheriger Beziehung:

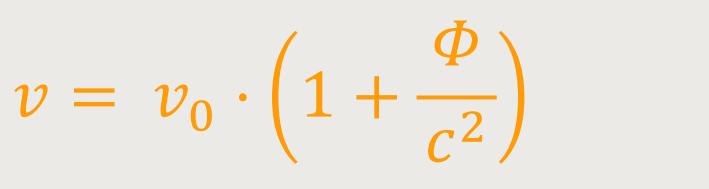
Wobei Φ die (negative) Gravitations­potential­differenz zwischen Sonnen­ober­fläche und Erde bedeutet. Nach Einsteins Auf­fassung müssen also die Spektral­linien des Sonnen­lichts gegen­über den entsprechenden Spektral­linien irdischer Licht­quellen etwas nach Rot verschoben sein, und zwar um den relativen Betrag:

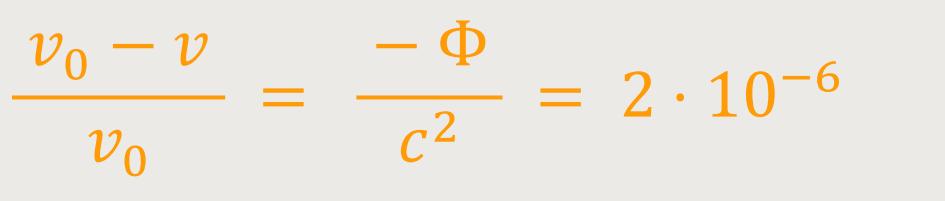
Einstein war davon überzeugt, wenn die Bedingungen, unter denen die Sonnen­strahlen ent­stehen, genau bekannt wären, ließe sich diese Verschiebung durch eine Messung nachweisen. Da aber ander­weitige Einflüsse, wie Druck und Temperatur die Lage des Schwer­punktes der Spektral­linien beeinflussen würden, sei es nach Einsteins Worten schwer vorher­zusagen, ob der hier abgeleitete Einfluss des Gravitations­potentials wirklich existiert.

An dieser Stelle bezieht sich Einstein auf L. F. Jewell, Ch. Fabry und H. Boisson, die in deren Abhand­lungen der­artige Verschie­bungen feiner Spektral­linien nach dem roten Ende des Spektrums, von Einsteins berechneten Größen­ordnung tatsäch­lich vorher­gesagt hatten, aber diese einer Wirkung des Druckes in der absorbierenden Schicht zugeschrieben hätten.

Bei oberflächlicher Betrachtung scheinen beide obigen Gleichungen (2) bzw. (2a) eine Absurdität auszusagen. Wie kann bei gleich­bleibender Licht­über­tragung von S₂ nach S₁, in S₁ eine andere Anzahl von Perioden pro Sekunde ankommen, als in S₂ emittiert wird? Einsteins Begründung lautet, wir können v₂ bzw. v₁ nicht als Frequenzen schlecht hin, also als Anzahl Perioden pro Sekunde ansehen, weil eine Zeit im System K noch nicht fest­gelegt wurde. Die Frequenz v₂ bedeutet die Anzahl Perioden, bezogen auf die Zeit­einheit der Uhr U in S₂, die Frequenz v₁ dagegen die Anzahl Perioden, bezogen auf die Zeit­einheit der gleich beschaffenen Uhr U in S₁.

Aus Einsteins Sicht zwingt uns nichts zu der Annahme, dass die in verschiedenen Gravitations­potentialen befind­lichen Uhren U als gleich rasch gehend aufgefasst werden müssen. Dagegen müsste die Zeit in K so definiert werden, dass die Anzahl der Wellen­berge und Wellen­täler, die sich zwischen S₂ und S₁ befinden, von dem Absolutwert der Zeit unabhängig ist. Weil der in Betracht gezogene Prozess natur­gemäß ein stationärer ist. Würde man diese Bedingung nicht erfüllen, so erhielte man eine Zeit­definition, bei deren Anwendung die Zeit explizit in die Natur­gesetze einginge, was nach Einsteins Empfinden sicher unnatürlich und unzweck­mäßig wäre.

Die Uhren in S₁ und S₂ geben nach Einsteins Schluss­folgerung also nicht beide die „Zeit” richtig an. Messen wir die Zeit in S₁ mit der Uhr U, so müssen wir die Zeit in S₂ mit einer Uhr messen, die 1 + Φ /c² langsamer läuft als die Uhr U, falls sie mit der Uhr U an derselben Stelle verglichen wird. Denn mit einer solchen Uhr gemessen ist die Frequenz des oben betrachteten Licht­strahls bei seiner Aussendung in S₂ (siehe 2a):

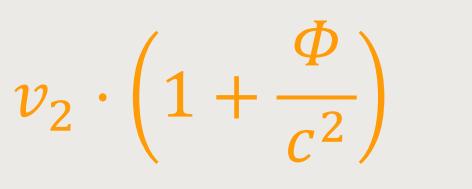
Somit ist die Frequenz gleich der Frequenz v₁ desselben Licht­strahls bei dessen Ankunft in S₁.

Für Einstein ergibt sich hieraus für diese Theorie eine Konsequenz von fundamentaler Bedeutung. Misst man nämlich in dem beschleu­nigten, gravitations­feld­freien System K' an verschiedenen Orten die Licht­geschwindig­keit unter Benutzung gleich­artiger Uhren U, so erhält man über­all dieselbe Größe. Dasselbe gilt nach vor­liegender Grund­annahme auch für das System K. Damit das aber mit dem oben Erwähnten konsistent ist, muss man sich an Stellen mit unter­schied­lichen Gravitations­potentialen auch verschieden beschaffener Uhren zur Zeit­messung bedienen.

Wir müssen also zur Zeit­messung an einem Ort, der relativ zum Koordinaten­ursprung das Gravitations­potential Φ besitzt, eine Uhr verwenden, die aus Sicht des Koordinaten­ursprungs, 1 + Φ/c² langsamer läuft als jene Uhr, mit welcher am Koordinaten­ursprung selbst die Zeit gemessen wird. Nennen wir c₀ die Licht­geschwindig­keit im Koordinaten­anfangs­punkt, so ergibt sich für die Licht­geschwindig­keit c in einem Orte vom Gravitations­potential Φ folgende Beziehung:

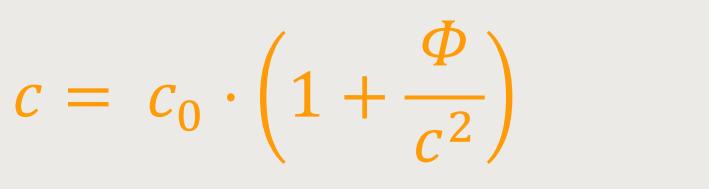
(Diese Beziehung wurde später gering­fügig korrigiert.)

Einstein gibt an dieser Stelle einen wichtigen Hinweis:

Das Prinzip von der Konstanz der Licht­geschwindig­keit gilt nach dieser Theorie nicht in derjenigen Fassung, wie es der Allgemeinen Relativitäts­theorie zugrunde gelegt zu werden pflegt.

Aus dem vorherigen Betrachtung, nämlich dass die Licht­geschwindig­keit im Schwere­feld eine Funktion des Ortes ist, lässt sich leicht mittels des Huygens-Fresnelschen Prinzips schließen, dass sich quer zu einem Schwere­feld fort­pflanzende Licht­strahlen eine Krümmung erfahren müssen.

Gekrümmte Licht­strahlen erinnerten Einstein an das nach dem holländischen Physiker Huygens benannte Prinzip, dass sich Licht stets den schnellsten Weg sucht, und nicht wie man zunächst meinen würde, den kürzesten. Damit erklärt sich zum Beispiel die Fähig­keit von Linsen, Licht­strahlen abzu­lenken und zu bündeln.

Galaxien­haufen etwa, die erst Jahr­zehnte später entdeckt wurden, scheinen beispiels­weise das Licht auf diese Weise zu bündeln ähnlich wie Sammel­linsen. Die Astronomen nennen sie heute „Gravitations­linsen”, ohne dass ihnen oftmals der unmittel­bare Zusammen­hang zu Einsteins Idee der variablen Licht­geschwindig­keit bewusst ist.

Um die Krümmung der Licht­strahlen zu verdeut­lichen, bediente sich Einstein einer Ebene. Gegeben sei eine Ebene ε mit gleicher Phase einer ebenen Licht­welle zur Zeit t. Des Weiteren seien P₁ und P₂ zwei Punkte in der Ebene, welche den Abstand 1 besitzen. Die Punkte P₁ und P₂ liegen so in der Papier­ebene, dass der in der Richtung ihrer Normale genommene Differential­quotient von Φ, und demnach auch von c verschwindet. Die entspre­chende Ebene gleicher Phase bzw. deren Schnitt mit der Papierebene, zu der Zeit t + dt erhält man, indem um die Punkte P₁ und P₂ mit den Radien c₁ · dt bzw. c₂ · dt Kreise gewogen werden und an diese eine Tangente anlegt wird, wobei c₁ bzw. c₂ die Licht­geschwindig­keit in den Punkten P₁ bzw. P₂ bedeutet. Der Krümmungs­winkel des Licht­strahls auf dem Wege c · dt ist demnach wie folgt definiert:

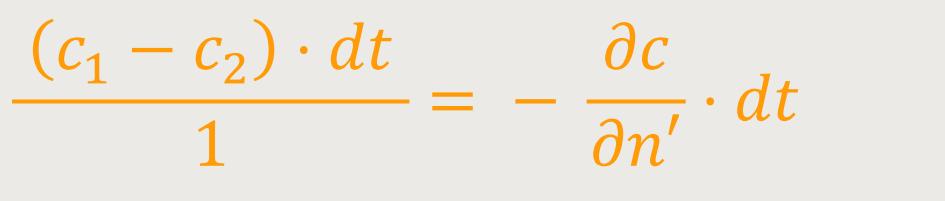
Wobei der Krümmungs­winkel einen positiven Wert erhält, wenn der Licht­strahl nach der Seite der wachsenden n' hin gekrümmt wird.

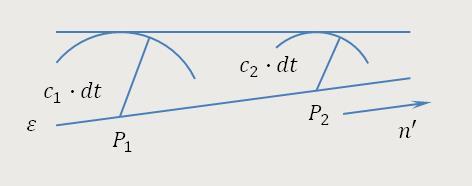
Abb. 3

Der Krümmungs­winkel pro Weg­einheit des Licht­strahls ist also:

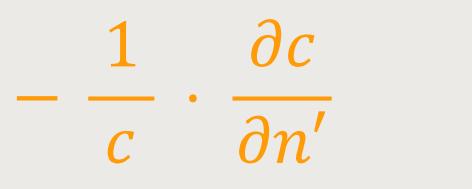
... oder bezug­nehmend auf (3) ergibt sich:

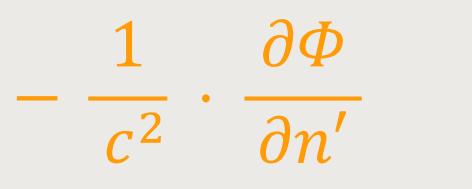
Abschließend erhält man mit dem Ablenkungs­winkel α, der beschreibt wie ein Licht­strahl auf einem beliebigen Wege (s) nach der Seite n' abgelenkt wird, den Ausdruck (4):

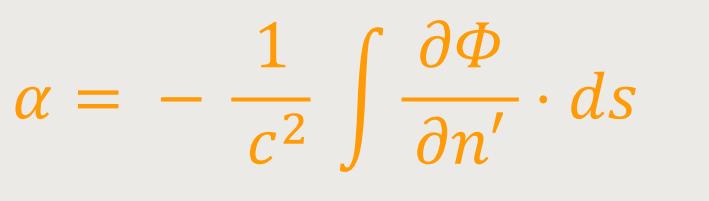
Dasselbe Resultat hätte man nach Einsteins Worten durch eine unmittel­bare Betrach­tung der Aus­breitung eines Licht­strahls in dem gleich­förmig beschleu­nigten System K' erhalten können. Und wenn man das Resultats auf das System K über­tragen hätte, sowie weiter auf die Situation, dass das Gravitations­feld beliebig gestaltet ist.

Nach Gleichung (4) vollzieht ein an einem Himmels­körper vorbei­gehender Licht­strahl eine Ablenkung, in Richtung der Seite des sinkenden Gravitations­potentials, also nach der dem Himmelskörper zugewandten Seite von der Größe:

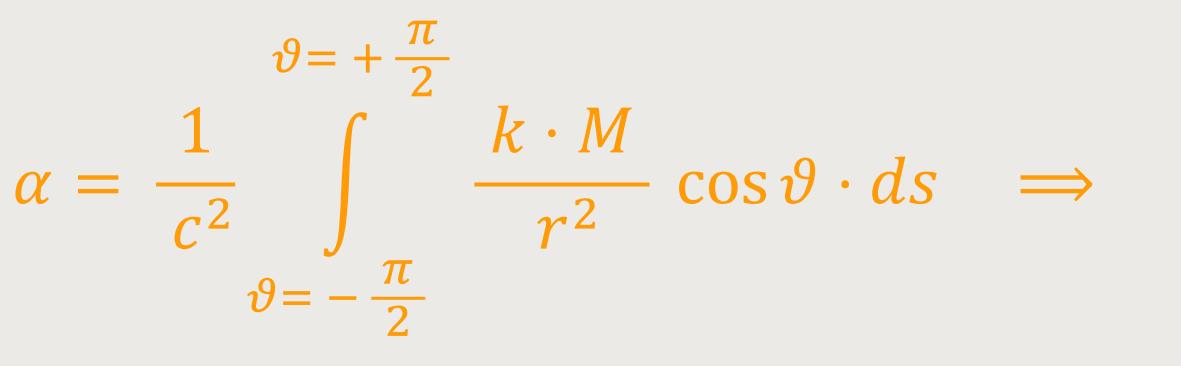
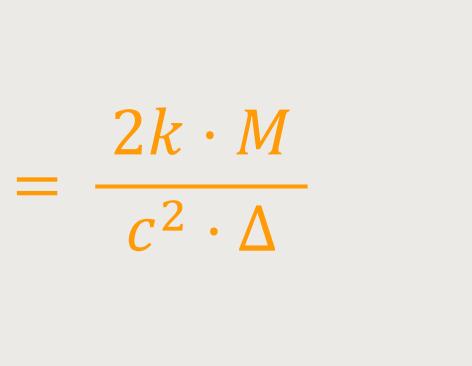
k    ist die Gravitationskonstante
M   ist die Masse des Himmelskörpers
Δ    ist der Abstand des Lichtstrahls vom Mittelpunkt des Himmelskörpers

Ein an der Sonne vorbei­gehender Licht­strahl voll­zieht demnach eine Ablenkung in der Größen­ordnung von 4 · 10⁻⁶ = 0,83 Bogen­sekunden. (Hier hatte sich Einstein um den Faktor 2 ver­rechnet.)

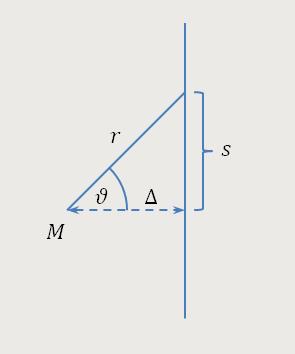
Abb. 4

Um diesen Betrag erscheint die Winkel­distanz des Sternes vom Sonnen­mittelpunkt durch die Krümmung des Strahls vergrößert. Da die Fix­sterne an der der Sonne zugewandten Himmels­partien bei totalen Sonnen­finster­nissen sichtbar werden, stimmt diese Schluss­folgerung der Theorie mit der Realität überein. Beim Planeten Jupiter erreicht die zu erwartende Verschie­bung etwa 1 /100 des angegebenen Betrags.

Einstein wünschte sich, dass sich Astronomen der hier aufgeworfenen Frage annähmen, auch wenn seine Über­legungen noch nicht ausreichend fundiert seien oder gar abenteuerlich erscheinen sollten. Denn abgesehen von jeder Theorie muss man sich fragen, ob sich mit den zur Zeit Einsteins zur Verfügung stehenden Mittel ein Einfluss der Gravitations­felder auf die Ausbreitung des Lichts hätte vorhersagen lassen.

⇦ Kapitel Kapitel ⇨