Die „Lichtbeugung” ist eng mit der Interferenz verbunden, wenngleich er auch andere Aspekte beinhaltet. Ein entscheidendes Prinzip, welches hier zur Anwendung kommt ist das huygens-fresnel'sche Prinzip.
Wir erinnern uns, dieses Prinzip sagt aus, dass jeder Punkt in einem Wellenfeld, welches von einer Primärwelle getroffen wird, als Ausgangspunkt einer neuen sekundären Kugelwelle aufgefasst werden kann. Als Folge davon wird sich eine Vielzahl von neuen Kugelwellen bilden.
Grafik (wird später eingefügt)
Die Einhüllende der in Reihe angeordneten Kugelwellen rufen im Anschluss wieder ebene Wellenzüge hervor. Abweichende Kugelwellen dagegen werden sich recht präzise durch destruktive Interferenz weginterferieren. Daher wird nur in einer eingeschränkten Vorwärtsrichtung eine weitere Ausbreitung erfolgen.
Wenn es im Nachfolgenden um Lichtbeugung geht, werden hierzu in diese ebenen Wellenfronten ein oder mehrere Hindernisse eingebracht. Im Bereich der Hindernisse wird dann verständlicherweise keine weitere Ausbreitung der Wellenfronten erfolgen. Man spricht bei einem solchen Hindernis auch von einer „Halbebene”, die undurchlässig für jegliche Wellenfronten ist.
Grafik (wird später eingefügt)
Im Bereich neben der Halbebene werden sich weiterhin Kugelwellen bilden. Diese werden aber nicht linear weiterlaufen, sondern ein gewisser Anteil der Lichtenergie wird auch in den abgeschatteten Bereich hineinreichen. In diesem Fall spricht man von einer „Beugung an der Kante”.
Grafik (wird später eingefügt)
Wenn die Distanzen zwischen mehreren Hindernissen sehr klein sind, wie zum Beispiel bei Spalten oder Gittern, richtet man die Geometrie möglichst so aus, dass weiterhin ein Parallelstrahl betrachtet werden kann. In diesem Fall spricht man von der „Fraunhofer'schen Beugung”. Die Parallelstrahlenbündel, die auf das Hindernis auftreffen, bleiben auch nach dem Hindernis erhalten. Insofern sind die geometrischen Verhältnisse viel übersichtlicher als bei der Fresnel'schen Beugung.
Daher möchten wir nachfolgend nochmals den Doppelspalt betrachten. Das Licht kommt hierbei aus großer Distanz, trifft aber dennoch im Bereich des Doppelspaltes parallel auf das Hindernis auf. Wenn man von einer großen Distanz spricht, dann groß im Vergleich zum Abstand eines Doppelspaltes.
Grafik (Folie) (wird später eingefügt)
Grafik (wird später eingefügt)
Wenn also mehrere Wellenfronten auf einen mit geringem Abstand vorhandenen Doppelspalt treffen, werden sich sekundäre Kugelwellen ausbilden.
d ist der Spaltabstand
b ist die Spaltbreite
s ist der Gangunterschied
Wenn hinter den Spalten derartige Kugelwellen weiter fortlaufen, gibt es einerseits eine geradlinige Ausbreitung, so wie bei einer ungestörten Wellenfront. Anderseits wird sich auch schräg in seitliche Richtung eine Ausbreitung ergeben, vor allem dann, wenn sich die beiden Wellen konstruktiv überlagern. Das ist deshalb so, weil sich die Wellen in der Art und Weise ausbreiten, dass der Gangunterschied s einer Wellenlänge λ, oder einem ganzzahligen Vielfachen z einer Wellenlänge, entspricht.
Insofern gibt es strahlenförmig zu den Seiten hin ebenfalls konstruktive
Interferenz. Bei der geradlinigen Ausbreitung spricht man von
Auf diese Weise ergeben sich Beugungsordnungen für verschiedene Gangunterschiede. Eine Verstärkung ist somit definiert als:
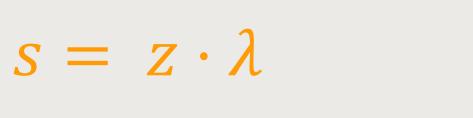
Je nach Beugungsordnung erhält man einen Winkel ϑ. Dieser steht mit den Gangunterschieden wie folgt in Beziehung:
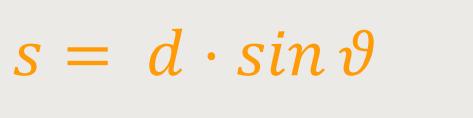
Durch Einsetzen erhält man die Bedingung für die Verstärkung beim Doppelspalt:
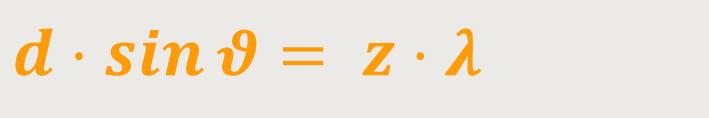
Grafik (Folie) (wird später eingefügt)
Wenn man das konkret durchrechnet, ergibt sich je nach Beugungswinkel eine entsprechende Intensität, die eine modulierte Sinusschwingung durchläuft. Nach außen hin werden die Beugungsordnungen schwächer. Und manche Beugungsordnungen treten überhaupt nicht auf, sodass letztlich nur wenig scharf ausgebildete Beugungsordnungen auftreten.
Grafik (Folie) (wird später eingefügt)
Bei mehr als zwei Spalten bildet der Spaltabstand d die „Gitterkonstante”. Der Gangunterschied zwischen den gebeugten Strahlen wird auch hier mit s bezeichnet. Und in gleicher Weise erhält man auch bei einem Gitter für verschiedene Gangunterschiede eine Verstärkung, die wie zuvor definiert ist als:
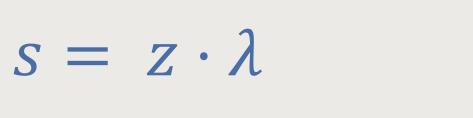
Die Beugungsordnung wird auch hier durch den Winkel ϑ definiert. Dieser steht mit den Gangunterschieden unverändert wie oben in Beziehung:
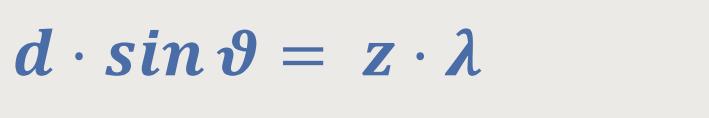
Allerdings ergibt sich jetzt der Unterschied, dass man hier keine Zweistrahl-Interferenz betrachtet, sondern eine „Vielstrahl-Interferenz”. In einem solchen Fall muss man eher damit rechnen, dass selbst bei kleinen Abweichungen von der Verstärkungsrichtung die einzelnen Strahlen bereits stärker beginnen aus der Phase zu laufen. Dementsprechend werden die Bereiche, bei denen Beugungsordnungen mit Verstärkung auftreten, in ihrer Breite eingeschränkt, und dazwischen fallen die Bereiche mit Abdunkelung größer aus.
Grafik (Folie) (wird später eingefügt)
Ähnlich wie beim Doppelspalt ergibt sich je nach Beugungswinkel eine entsprechende Intensität, bei der nach außen hin die Beugungsordnungen immer schwächer werden. Auch hier treten manche Beugungsordnungen überhaupt nicht auf. Je mehr Beugungsordnungen man betrachtet, desto mehr nimmt die Anzahl der Sekundärwellen zwar zu, aber umso schärfer treten die Verstärkungen und Maxima auf.
Um ein derartiges Beugungsverhalten am Gitter auszuwerten, bietet sich zum einen die Strukturanalyse an. Wenn die Wellenlänge λ der einfallenden Welle bekannt ist, beispielsweise bei einem Laser, und auch der Beugungswinkel ϑ bekannt ist, lässt sich die Gitterkonstante d ausrechnen.
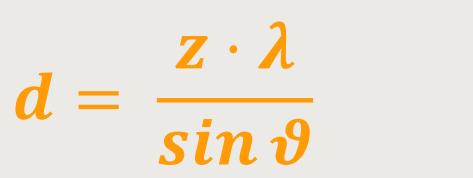
Umgekehrt ist es auch möglich, Spektrometrie zu betreiben, indem bei bekanntem Beugungswinkel und bekannter Gitterkonstante die Wellenlänge ermittelt wird:
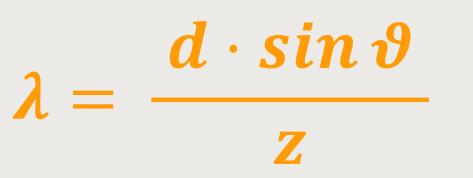
Beschränkt man sich nur auf die erste Beugungsordnung, entspricht
Wenn es um ein Licht geht, in welchem mehrere Wellenlängen enthalten sind, verlaufen die Beugungsordnungen der einzelnen Wellenlängen in unterschiedliche Richtungen. Eine besonders gute Auflösung erhält man, wenn die Beugungsordnungen schmal genug sind.
Wird statt einer monochromatischen Lichtquelle eine weiße Lichtquelle verwendet, wird die nullte Ordnung in der Mitte des Beugungsmusters mit einem weißen Lichtbalken dargestellt. Das liegt daran, weil dort alle Wellenlängen mit Beugungswinkel Null zusammentreffen und in Summe wieder ein weißes Licht ergeben.
Wogegen es seitlich mit zunehmenden Beugungsordnungen zu entsprechenden Überlagerungen der Wellen kommt, mit deren typischen Spektralfarben. In der ersten Beugungsordnung lässt sich gut erkennen, dass rotes Licht einen größeren Beugungswinkel hat, und dass blaues Licht einen kleineren Beugungswinkel besitzt.
An einem Prisma lässt sich gut beobachten, dass die kurzen Wellenlängen stärker gebrochen werden, und damit der Brechungsindex größer ist. Allerdings ist hierbei zu berücksichtigen, dass in Verbindung mit einem Prisma nicht von Interferenz oder Beugung die Rede ist, sondern nur von „Brechung” des Lichtes.
Deswegen sind die Farben am Prisma gegenüber dem Gitter anders angeordnet. Bei der Lichtbeugung liegt der rote Farbbalken außen, wogegen bei der „Lichtbrechung” am Prisma der blaue bzw. violette Farbbalken außen liegt.
Darüber hinaus gibt es noch eine weitere wichtige Anwendung der Lichtbeugung. Aufgrund der Lichtbeugung an Hindernissen kann man auch abschätzen, wo die Grenzen bei optischen Geräten liegen.
Um zu erkennen, wo die Anwendungsbereiche der Wellenoptik liegen, wollen wir uns zunächst noch einmal die Funktionsweise eines Mikroskops in Erinnerung rufen.
Das Mikroskop fällt in den Bereich der Optik. Doch die geometrische Optik hat nur in den Bereichen ihre Gültigkeit, bei der die Objekte groß genug sind gegenüber den Lichtwellenlängen. Wenn es dagegen um Objekte in der Größenordnung der Lichtwellenlänge selbst geht, setzt der Aspekt der Wellenoptik und der Beugung des Lichtes ein.
Grafik (wird später eingefügt)
Ausgehend von einer Lichtquelle, dessen Licht zunächst auf eine Sammellinse bzw. einen Kondensor trifft, wird anschließend ein paralleles Lichtstrahlenbündel auf ein zu betrachtendes Objekt gelenkt. Hinter dem Gegenstand befindet sich eine Objektivlinse, dessen Brennweite etwas kleiner ist, als der Abstand des Gegenstandes zum Objektiv. Typischerweise kann der Gegenstand bei einer solchen Betrachtung durchleuchtet werden.
Hinter der Objektivlinse wird das Objekt dann entsprechend der Strahlengeometrie vergrößert dargestellt. Zur nochmaligen Vergrößerung des betrachteten Objektes befindet sich hinter der Bildebene ein Okular, welches im Wesentlichen einer Lupe entspricht. Auf diese Weise wird das reelle Bild mehrfach vergrößert dargestellt.
Worauf es uns hier besonders ankommt, ist die Art und Weise, wie durch eine solche Linsen-Anordnung ein Gegenstand vergrößert dargestellt werden kann. Allerdings sind mit einer solchen Vorrichtung dem Auflösungsvermögen recht bald Grenzen gesetzt.
Um dieser Frage näher auf den Grund zu gehen, werden wir den Vorgang nicht aus Sicht des Strahlenaspektes darstellen, sondern Aufgrund des Wellenaspektes. Hierzu betrachtet man mit dem Mikroskop ein Gitter und untersucht, bis zu welchen Gitterkonstanten dieses Gitter noch aufgelöst werden kann.
Grafik (wird später eingefügt)
Auch hierbei geht von einer Lichtquelle ein Lichtstrahl aus, der mittels eines Kondensors ein Lichtstrahlenbündel bewirkt. Im weiteren Verlauf trifft der Strahl jetzt auf ein Gitter, sodass nun die Fraunhofer'sche Beugung zum Tragen kommt. Im Anschluss befindet sich ebenfalls eine Objektivlinse, dessen Brennweite etwas kleiner ist, als der Abstand des Gitters von dem Objektiv. Analog zu oben wird die Objektivlinse die Gitterstruktur hinter der Linse in einem reellen und vergrößerten Bild auf der Bildebene darstellen.
Es stellt sich jetzt die Frage, wie wird es aus Sicht der Beugung zu einer Abbildung an dem Gitter kommen?
Zunächst gibt es, wie nicht anders zu erwarten, ein Parallelstrahlenbündel der nullten Ordnung. Und dieses Strahlenbündel wird im Brennpunkt der Objektivlinse auf der Brennebene gesammelt. Aber es gibt auch gemäß der Fraunhofer'schen Beugung schräg verlaufende Strahlen, die zusätzlich Parallelstrahlenbündel der ersten Ordnung erzeugen und auf der Brennebene zusammenlaufen. Weitere Parallelstrahlenbündel höherer Ordnungen rufen ihrerseits ebenfalls versetzte Brennpunkte hervor. Zwischen den Brennpunkten gibt es daher Schattenbereiche.
Als Ergebnis erhält man also kohärente Lichtquellen auf der Brennebene, die anschließend in der Bildebene so interferieren, dass dort ein Bild des Gegenstandes entsteht. Ein Bild wird aber nur dann erzeugt, wenn zumindest die erste Beugungsordnung vorhanden ist. Je feiner die Gitterstruktur, desto größer wird die Spreizung der höheren Ordnungen.
Denn wenn in obiger Beziehung die Gitterkonstante d kleiner wird, muss der Beugungswinkel ϑ bei gleicher Wellenlänge größer werden. In Grenzsituationen hat das zur Folge, dass die Lichtstrahlen möglicherweise die Objektivlinse nicht mehr treffen. Und wenn in einem solchen Fall nicht einmal die erste Beugungsordnung zustande kommt, sieht man nichts, außer einer gleichmäßigen Beleuchtung in der Bildebene.
Im Umkehrschluss heißt das demnach, je mehr Beugungsordnungen auftreten, desto schärfer wird das Bild. Was wird nun das kleinste auflösbare Detail sein? In der ersten Beugungsordnung lässt sich das definieren als:
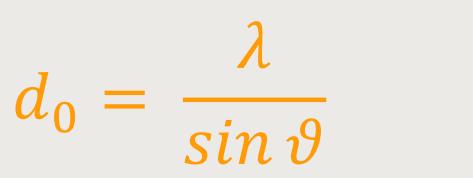
Grafik (wird später eingefügt)
Aus diesem Grund haben Mikroskope möglichst kleine Brennweiten. Dadurch wird trotz größerem Beugungswinkel aus Sicht des Objektivs das Auflösungsvermögen feiner und feiner. Beim Mikroskop ist also nicht die Vergrößerung entscheidend, sondern das Auflösungsvermögen.
Das Auflösungsvermögen wird daher definiert als:
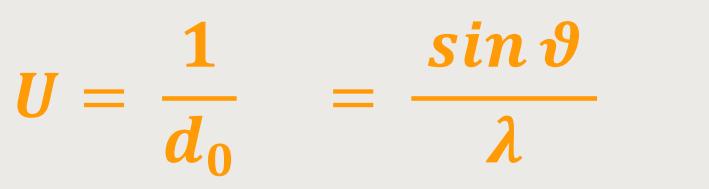
Aus dieser Beziehung, die auf den Physiker Ernst Abbe zurückgeht, lässt sich erkennen, dass man mittels eines Elektronenstrahls die Wellenlänge um mehrere Größenordnungen heruntersetzen kann, nämlich auf die De-Broglie-Wellenlänge von Elektronen. Der Nachteil ist allerdings, dass man hierfür Sensoren benötigt, um eine Abbildung des Gegenstandes sichtbar zu machen. Und mit Glaslinsen ist das auch nicht mehr zu bewerkstelligen.
Da die Elektronen aber eine negative Elementarladung besitzen, lassen sich mit Hilfe entsprechender Magnetfelder diese Elektronen umlenken. Das sind dann quasi „magnetische” Linsen, die den Elektronenstrahl ausrichten und einen ähnlichen Abbildungsvorgang erzielen, wie bei den Lichtmikroskopen.
Die Auflösung ist mittlerweile so gut, dass atomare Kristallstrukturen mit den einzelnen Gitteratomen sichtbar gemacht werden können. Auf diese Weise konnten theoretische Modelle über die Gitterstrukturen konkret bestätigt werden.
Hier sei noch erwähnt, dass sich die ganze Betrachtung im Hochvakuum abspielt, und deshalb nur solche Objekte genauer untersucht werden können, die vakuumgeeignet sind. Insofern sind neuere Technologien wie die Röntgenlaser auch nur bedingt einsetzbar, weil diese schädlichen Einfluss auf die Objekte nehmen.
In gleicher Weise kommt es bei den klassischen Fernrohren auf den Radius der Eingangsöffnung an, wie gut das Auflösungsvermögen ist. Da dies aber bei zunehmender Größe, unter anderem wegen der Schwingungen, mit Glaslinsen nicht mehr zu realisieren ist, sind alle großen Teleskope auf dem Prinzip des Parabolspiegels aufgebaut.
Deshalb sind auch die Weltraumteleskope Spiegelteleskope, die als Objektiv einen Hohlspiegel besitzen.
⇦ Kapitel Kapitel ⇨
