Man könnte das wie folgt veranschaulichen:
Wir betrachten einen Beobachter (B), der sich Informationen verschafft über ein System (S). Er macht also dort eine Messung. Der Beobachter (B) wird immer als ein makrosko­pisches System angesehen. Das (B) und das (S) bilden zusammen ebenfalls wieder ein System, welches eine Umgebung und eine Begrenzung hat. Zwischen (B) und (S) gibt es Wechsel­wirkungen, und es gibt anschließend einen Messvorgang.

Also, (B) ist immer makros­kopisch. Wobei es natürlich interessant ist heraus­zufinden, wo hören die klassischen Gesetz­mäßig­keiten auf und wo fangen die quanten­mechanischen Gesetz­mäßig­keiten an. Wenn man ein einzelnes Molekül betrachtet, wird dies eindeutig von den quanten­mechanischen Gesetz­mäßig­keiten bestimmt. Betrachtet man dagegen ein Stück Masse, dann handelt es sich hierbei um ein klassisches System. Und irgendwo dazwischen muss es den Übergang von dem einen in das andere System geben.

Falls das System (S) auch makros­kopisch ist, was zum Beispiel in der Thermo­dynamik und in der Elektro­dynamik der Fall ist, dann ist der Einfluss des Beobachters (B) auf das System unterge­ordneter Natur. Man kann davon ausgehen, dass die Messung auf das beobachtete System einen sehr geringen und oft vernachlässig­baren Einfluss hat. In einem solchen Fall spricht man auch von objektiven System­eigenschaften. Mit andern Worten, es wird eine objektive Wirklichkeit abgebildet.

Denn in dem Moment, wo durch eine Messung ein wesent­licher Einfluss auf das System ausgeübt wird, hat dies Auswirkungen auf die objektive Wirklichkeit. Je nachdem, welche Messung man vornimmt und welches Ergebnis man dementsprechend erhält, ist die Basis für das, was man allgemein als objektive System­eigenschaften oder eine objektive Wirklichkeit ansieht. Letztlich geht es bei dem Messvorgang immer darum, inwieweit man einem System eine objektive Wirklichkeit zuordnen kann.

Wenn sich das aber im Mikrokosmos abspielt, also in Größen­ordnungen von Atomen oder Molekülen, dann kann es passieren, wenn man zu scharf hinschaut, dass sich die betrachteten Teilchen auf einmal woanders befinden. Daraus resultieren dann Begriffe wie die Unschärfe­relation. Die Sache beginnt undeutlich zu werden, in dem Sinne, dass man unter Umständen keine objektive Wirklichkeit mehr definieren kann. Die Wirklichkeit wird dann durch den Messvorgang mitbestimmt. Der Messvorgang selbst beeinflusst in einem solchen Fall das System. Falls also das System mikros­kopisch ist, dann wird es immer einen wesentlichen Einfluss von (B) auf (S) geben.

Die Heisenbergsche Unschärferelation, die das zu beschreiben erlaubt, lautet:

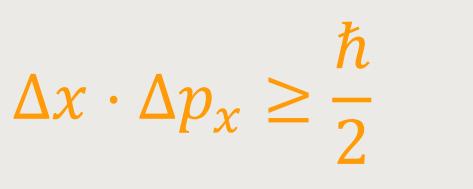
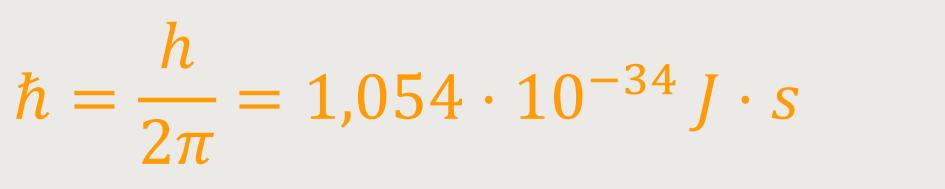
ℏ  ist das Plancksche Wirkungsquantum

Messungen einer objektiven Wirklichkeit ohne Beeinflussung des beobachteten Systems sind dann nicht mehr durchführbar.

Systeme beschreibt man immer mit physika­lischen Größen. Hierfür definiert man sich solche Größen, die sich als besonders nützlich erweisen. Die Auswahl solcher Größen ist abhängig von dem jeweils verwendeten Modell, aber an sich willkürlich. Die „Kraft” ist zum Beispiel nichts anderes als die Ursache für eine Beschleunigung eines Systems. Wenn sich ein System beschleunigt bewegt, dann muss auf dieses System eine Kraft wirken. Die Kraft gibt dann an, wie groß diese Beschleunigung ist.

Wenn man anschließend eine Messung dieser Größen durchführt, vergleicht man zwei „gleichartige” Größen. Der Vergleich dieser beiden Größen bestimmt das Ergebnis. Die Vergleichs­größe ist demnach die Einheit. Und die Größe, um die es im Einzelfall geht (Länge, Masse, Zeit usw.), wird abgeleitet aus der Maßzahl multipliziert mit der Einheit. Eine wichtige Eigenschaft von Messungen ist vor allem die Reproduzier­barkeit dieser Messungen. Erst dann hat ein Experiment eine Gültigkeit.

Eine Physikalische Relation ist einer Relation zwischen physikalischen Größen. Wobei die Größe gleich Maßzahl · Einheit ist (10m, 60s usw.). Es gibt auch eine Relation zwischen den Maßzahlen.

Damit das Ganze aber übersichtlich ist, führt man ein System von bestimmten vorgegebenen Einheiten ein. Um ein solches System einführen zu können, benötigt man zunächst „Basis­größen”, die aus einem solchen System heraus­genommen werden. Diese Basis­größen können auch als Grund­größen angesehen werden.

⇦ Kapitel Kapitel ⇨